
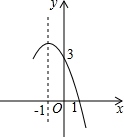 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论:| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
分析 由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
解答 解:①由图知:抛物线与x轴有两个不同的交点,则△=b2-4ac>0,∴b2>4ac,故①正确;
②抛物线开口向下,得:a<0;
抛物线的对称轴为x=-$\frac{b}{2a}$=-1,b=2a,故b<0;
抛物线交y轴于正半轴,得:c>0;
所以abc>0;
故②正确;
③∵抛物线的对称轴为x=-$\frac{b}{2a}$=-1,b=2a,
∴2a-b=0,故③正确;
④根据b=2a可将抛物线的解析式化为:y=ax2+2ax+c(a≠0);
由函数的图象知:当x=2时,y<0;即4a+4a+c=8a+c<0,故④正确;
⑤由函数的图象知:当x=3时,y<0;所以9a+3b+c<0;故⑤正确;
所以这结论正确的有①②③④⑤.
故选D.
点评 此题主要考查了图象与二次函数系数之间的关系,会利用对称轴的范围求2a与b的关系,以及二次函数与方程之间的转换,根的判别式的熟练运用.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案科目:初中数学 来源: 题型:填空题
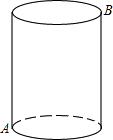 如图所示,一个圆柱体的高为6cm,底面半径为$\frac{8}{π}$cm,在圆柱体下底面A点有一只蚂蚁,想吃到上底面B点的一粒砂糖(A、B是圆柱体上、下底面相对的两点),则这只蚂蚁从A出点沿着圆柱表面爬到B点的最短路线的长是10cm.
如图所示,一个圆柱体的高为6cm,底面半径为$\frac{8}{π}$cm,在圆柱体下底面A点有一只蚂蚁,想吃到上底面B点的一粒砂糖(A、B是圆柱体上、下底面相对的两点),则这只蚂蚁从A出点沿着圆柱表面爬到B点的最短路线的长是10cm.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=x2+3 | B. | y=x2-4x+3 | C. | y=x2-6x+11 | D. | y=x2-6x+8 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图所示,已知△ABC和△DCE均是等边三角形,点B,C,E在同一条直线上,AE与BD交于点O,AE与CD交于点G,AC与BD交于点F,连接OC,FG,则下列结论中:①AE=BD;②AG=BF;③FG∥BE.其中正确结论的个数( )
如图所示,已知△ABC和△DCE均是等边三角形,点B,C,E在同一条直线上,AE与BD交于点O,AE与CD交于点G,AC与BD交于点F,连接OC,FG,则下列结论中:①AE=BD;②AG=BF;③FG∥BE.其中正确结论的个数( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com