
【题目】在平面直角坐标系中,已知直线![]() 的参数方程为
的参数方程为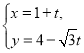 (
(![]() 是参数),以原点为极点,
是参数),以原点为极点,![]() 轴的非负半轴
轴的非负半轴
为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设点![]() 在曲线
在曲线![]() 上,曲线
上,曲线![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 垂直,求点
垂直,求点![]() 的直角坐标.
的直角坐标.
【答案】(Ⅰ)![]() ,
,![]() ;(Ⅱ)
;(Ⅱ)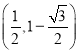 或
或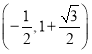
【解析】
(Ⅰ)根据直线参数方程消去参数,即可求出直线普通方程;根据极坐标与直角坐标的互化公式,即可求出直角坐标方程;
(Ⅱ)设点![]() ,根据题意,得到
,根据题意,得到![]() ,再由点
,再由点![]() 在曲线
在曲线![]() :
:![]() 上,列出方程组,求解,即可得出结果.
上,列出方程组,求解,即可得出结果.
(Ⅰ)由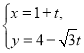 消去参数
消去参数![]() ,得
,得![]() ,即
,即![]() ,
,
所以直线![]() 的普通方程是
的普通方程是![]() .
.
由![]() ,得
,得![]() ,
,
根据公式![]() 得
得![]() ,所以曲线
,所以曲线![]() 的直角坐标方程是
的直角坐标方程是![]() .
.
(Ⅱ)对于直线![]() 的参数方程为
的参数方程为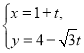 (
(![]() 是参数),因为
是参数),因为![]() ,所以直线
,所以直线![]() 的斜率是
的斜率是![]() .
.
因为曲线![]() 在
在![]() 处的切线与直线
处的切线与直线![]() 垂直,又曲线
垂直,又曲线![]() 在
在![]() 处的切线与
处的切线与![]() 垂直,
垂直,
所以直线![]() 与直线
与直线![]() 平行.
平行.
所以直线![]() 与直线
与直线![]() 的斜率相等.所以直线
的斜率相等.所以直线![]() 的斜率
的斜率![]() .
.
设点![]() ,则
,则![]() ,整理得
,整理得![]() .
.
又因为点![]() 在曲线
在曲线![]() :
:![]() 上,
上,
所以其坐标必然满足曲线![]() 的方程:
的方程:![]() ,代入得
,代入得![]() .
.
联立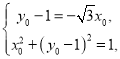 解得
解得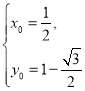 或
或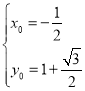 .
.
所以点![]() 的直角坐标为
的直角坐标为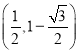 或
或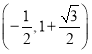


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() ,若
,若![]() 的图象上相邻两条对称轴的距离为
的图象上相邻两条对称轴的距离为![]() ,图象过点
,图象过点![]() .
.
(1)求![]() 的表达式和
的表达式和![]() 的递增区间;
的递增区间;
(2)将函数![]() 的图象向右平移
的图象向右平移![]() 个单位长度,再将图象上各点的横坐标伸长到原来的2倍(纵坐标不变),得到函数
个单位长度,再将图象上各点的横坐标伸长到原来的2倍(纵坐标不变),得到函数![]() 的图象.若函数
的图象.若函数![]() 在区间
在区间![]() 上有且只有一个零点,求实数
上有且只有一个零点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学高三(3)班有学生50人,现调查该班学生每周平均体育锻炼时间的情况,得到如下频率分布直方图,其中数据的分组区间为:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
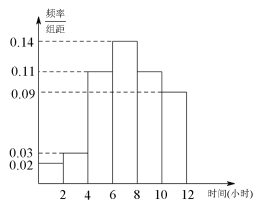
(1)从每周平均体育锻炼时间在![]() 的学生中,随机抽取2人进行调查,求这2人的每周平均体育锻炼时间都超过2小时的概率;
的学生中,随机抽取2人进行调查,求这2人的每周平均体育锻炼时间都超过2小时的概率;
(2)已知全班学生中有40%是女姓,其中恰有3个女生的每周平均体育锻炼时间不超过4小时,若每周平均体育锻炼时间超过4小时称为经常锻炼,问:有没有90%的把握说明,经常锻炼与否与性别有关?
附:![]()
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】直线l:x﹣ty+1=0(t>0)和抛物线C:y2=4x相交于不同两点A、B,设AB的中点为M,抛物线C的焦点为F,以MF为直径的圆与直线l相交另一点为N,且满足|MN|![]() |NF|,则直线l的方程为_____.
|NF|,则直线l的方程为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,已知直线![]() 的参数方程为
的参数方程为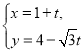 (
(![]() 是参数),以原点为极点,
是参数),以原点为极点,![]() 轴的非负半轴
轴的非负半轴
为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设点![]() 在曲线
在曲线![]() 上,曲线
上,曲线![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 垂直,求点
垂直,求点![]() 的直角坐标.
的直角坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年以来,世界经济和贸易增长放缓,中美经贸摩擦影响持续显现,我国对外贸易仍然表现出很强的韧性.今年以来,商务部会同各省市全面贯彻落实稳外贸决策部署,出台了一系列政策举措,全力营造法治化、国际化、便利化的营商环境,不断提高贸易便利化水平,外贸稳规模、提质量、转动力取得阶段性成效,进出口保持稳中提质的发展势头,下图是某省近五年进出口情况统计图,下列描述正确的是( )
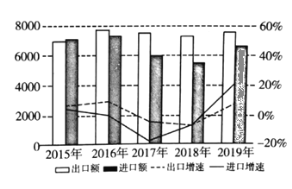
A.这五年,2015年出口额最少B.这五年,出口总额比进口总额多
C.这五年,出口增速前四年逐年下降D.这五年,2019年进口增速最快
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从分别写有数字1,2,3,4,5的5张卡片中随机抽取1张,放回后再随机抽取1张,则抽得的第一张卡片上的数字不大于第二张卡片的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某科研小组为了研究一种治疗新冠肺炎患者的新药的效果,选50名患者服药一段时间后,记录了这些患者的生理指标![]() 和
和![]() 的数据,并统计得到如下的
的数据,并统计得到如下的![]() 列联表(不完整):
列联表(不完整):
|
| 合计 | |
| 12 | 36 | |
| 7 | ||
合计 |
其中在生理指标![]() 的人中,设
的人中,设![]() 组为生理指标
组为生理指标![]() 的人,
的人,![]() 组为生理指标
组为生理指标![]() 的人,他们服用这种药物后的康复时间(单位:天)记录如下:
的人,他们服用这种药物后的康复时间(单位:天)记录如下:
![]() 组:10,11,12,13,14,15,16
组:10,11,12,13,14,15,16
![]() 组:12,13,15,16,17,14,25
组:12,13,15,16,17,14,25
(Ⅰ)填写上表,并判断是否有95%的把握认为患者的两项生理指标![]() 和
和![]() 有关系;
有关系;
(Ⅱ)从![]() ,
,![]() 两组随机各选1人,
两组随机各选1人,![]() 组选出的人记为甲,
组选出的人记为甲,![]() 组选出的人记为乙,求甲的康复时间比乙的康复时间长的概率.
组选出的人记为乙,求甲的康复时间比乙的康复时间长的概率.
附: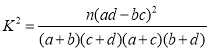 ,其中
,其中![]() .
.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com