
【题目】已知![]() ,函数
,函数 ,
,![]() ,若函数
,若函数![]() 有4个零点,则实数
有4个零点,则实数![]() 的取值范围是______.
的取值范围是______.
【答案】![]()
【解析】
画出函数![]() 的图像,对
的图像,对![]() 分成
分成![]() ,
,![]() 等
等![]() 种情况,研究
种情况,研究![]() 零点个数,由此求得
零点个数,由此求得![]() 的取值范围.
的取值范围.
令![]() ,画出函数
,画出函数![]() 的图像如下图所示,由图可知,
的图像如下图所示,由图可知,
(1)当![]() 或
或![]() 时,存在唯一
时,存在唯一![]() ,使
,使![]() ,而
,而![]() 至多有两个根,不符合题意.
至多有两个根,不符合题意.
(2)当![]() 时,由
时,由![]() 解得
解得![]() ,由
,由![]() 化简得
化简得![]() ,其判别式为正数,有两个不相等的实数根;由
,其判别式为正数,有两个不相等的实数根;由![]() 化简得
化简得![]() ,其判别式为正数,有两个不相等的实数根.由于上述四个实数根互不相等,故
,其判别式为正数,有两个不相等的实数根.由于上述四个实数根互不相等,故![]() 时,符合题意.
时,符合题意.
(3)当![]() 时,由
时,由![]() 解得
解得![]() ,由
,由![]() 化简得
化简得![]() ,其判别式为负数,没有实数根;由
,其判别式为负数,没有实数根;由![]() 化简得
化简得![]() ,其判别式为正数,有两个不相等的实数根.故当
,其判别式为正数,有两个不相等的实数根.故当![]() 时,不符合题意.
时,不符合题意.
(4)当![]() 时,由
时,由![]() ,根据图像可知有三个解,不妨设
,根据图像可知有三个解,不妨设![]() .
.
即
即 .
.
i)当![]() 时,
时, ,故①②③三个方程都分别有
,故①②③三个方程都分别有![]() 个解,共有
个解,共有![]() 个解,不符合题意.
个解,不符合题意.
ii)当![]() 时,
时, ,①有
,①有![]() 个解,②③分别有
个解,②③分别有![]() 个解,共有
个解,共有![]() 个解,不符合题意.
个解,不符合题意.
iii)当![]() 时,
时, ,①无解,②③分别有
,①无解,②③分别有![]() 个解,共有
个解,共有![]() 个解,符合题意.
个解,符合题意.
iv)当![]() 时,
时, ,①无解,②有
,①无解,②有![]() 个解,③有两个解,共有
个解,③有两个解,共有![]() 个解,不符合题意.
个解,不符合题意.
v)当![]() 时,
时, ,①无解,②无解,③至多有
,①无解,②无解,③至多有![]() 个解,不符合题意.
个解,不符合题意.
综上所述,![]() 的取值范围是
的取值范围是![]() .
.



 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 和
和![]() 的直角坐标方程;
的直角坐标方程;
(2)已知直线![]() 与
与![]() 轴交于点
轴交于点![]() ,且与曲线
,且与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,以坐标原点为极点,
中,以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程是
的极坐标方程是![]() ,曲线
,曲线![]() 的参数方程为:
的参数方程为: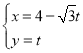 (
(![]() 为参数).
为参数).
(1)求曲线![]() ,
,![]() 的直角坐标方程;
的直角坐标方程;
(2)设曲线![]() ,
,![]() 交于点
交于点![]() ,
,![]() ,已知点
,已知点![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题![]() :关于
:关于![]() 的不等式
的不等式![]() 无解;命题
无解;命题![]() :指数函数
:指数函数![]() 是
是![]() 上的增函数.
上的增函数.
(1)若命题![]() 为真命题,求实数
为真命题,求实数![]() 的取值范围;
的取值范围;
(2)若满足![]() 为假命题且
为假命题且![]() 为真命题的实数
为真命题的实数![]() 取值范围是集合
取值范围是集合![]() ,集合
,集合![]() ,且
,且![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋中装有9只球,其中标有数字1,2,3,4的小球各2个,标数字5的小球有1个.从袋中任取3个小球,每个小球被取出的可能性都相等,用![]() 表示取出的3个小球上的最大数字.
表示取出的3个小球上的最大数字.
(1)求取出的3个小球上的数字互不相同的概率;
(2)求随机变量![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥A-BCDE中,![]() 平面BCDE,底面BCDE为直角梯形,
平面BCDE,底面BCDE为直角梯形,![]() 、
、![]() ,
,![]() ,F为AC上一点,且
,F为AC上一点,且![]() .
.
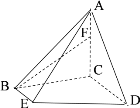
(1)求证:![]() 平面ADE;
平面ADE;
(2)求异面直线AB、DE所成角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com