
| 单价x(元) | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
| 销量y(件) | 90 | 84 | 83 | 80 | 75 | 68 |
分析 由题意求出$\overline{x}$,$\overline{y}$,利用公式求出$\hat{a}$,即可得出线性回归方程,当x=9.5时,可得结论.
解答 解:由题意:$\overline{x}$=$\frac{1}{6}(8+8.2+8.4+8.6+8.8+9)$=8.5;
$\overline{y}$=$\frac{1}{6}(90+84+83+80+75+68)$=80.
∵$\hat{b}$=-20.
∴$\hat{a}$=80+20×8.5=250,
从而得到回归直线方程为:y=-20x+250.
当x=9.5时,可得y=60.
故答案为:60.
点评 本题考查了线性回归方程的求法及应用,属于基础题.


 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若a>b,则ac≤bc | B. | 若ac≤bc,则a≤b | C. | 若ac>bc,则a>b | D. | 若a≤b,则ac≤bc |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
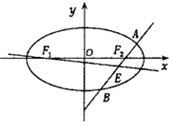 已知椭圆C的方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的一条渐近线与x轴所成的夹角为30°,且双曲线的焦距为4$\sqrt{2}$.
已知椭圆C的方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的一条渐近线与x轴所成的夹角为30°,且双曲线的焦距为4$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0对 | B. | 1对 | C. | 2对 | D. | 4对 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com