
分析 (1)抛物线y2=2px(p>0)的焦点恰是椭圆$\frac{x^2}{4}+\frac{y^2}{3}=1$的一个焦点,即$\frac{p}{2}=1,p=2$,即可;
(2)由直线L的倾斜角求得斜率,由点斜式得到直线L的方程,和抛物线方程联立后利用根与系数关系得到A,B的横坐标的和,代入抛物线的弦长公式得答案.
解答 解:(1)∵抛物线y2=2px(p>0)的焦点恰是椭圆$\frac{x^2}{4}+\frac{y^2}{3}=1$的一个焦点,∴$\frac{p}{2}=1,p=2$,
∴抛物线的方程为:y2=4x.
(2))∵直线L倾斜角为60°,∴其斜率为tan60°=$\sqrt{3}$,又抛物线的焦点坐标为T(1,0),
则直线L的方程为:y-0=$\sqrt{3}$(x-1)).
由$\left\{\begin{array}{l}{y=\sqrt{3}x-\sqrt{3}}\\{{y}^{2}=4x}\end{array}\right.$得3x2-10x+3=0.
设A(x1,y1),B(x2,y2).
则x1+x2=$\frac{10}{3}$,∴|AB|=${x}_{1}+{x}_{2}+p=\frac{10}{3}+2=\frac{16}{3}$.
点评 本题考查了抛物线的定义和方程,考查了直线与圆锥曲线的关系,涉及直线与圆锥曲线的关系问题,常采用联立方程组,化为关于x的方程后利用一元二次方程根与系数的关系解决,是中档题.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{2}}{2}$ | B. | 1 | C. | $\sqrt{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-1<x<3} | B. | {x|-3<x<1} | C. | {x|-1<x<1} | D. | {x|-3<x<3} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{6}$ | B. | $\sqrt{3}$-1 | C. | $\frac{\sqrt{3}}{2}$ | D. | 2-$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2,+∞) | B. | (0,2) | C. | $({0,\frac{4}{3}})$ | D. | $({\frac{4}{3},2})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2,+∞) | B. | (4,+∞) | C. | (-∞,2) | D. | (-∞,4) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
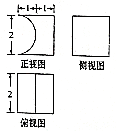 我国古代数学家祖暅提出的祖暅原理:“幂势既同,则积不容异”(“幂”是截面积,“势”是几何体的高),意思是两个同高的几何体,如在等高处截面的面积恒相等,则它们的体积相等.已知某不规则几何体与三视图(如图所示)所表示的几何体满足“幂势既同”,则该不规则几何体的体积为( )
我国古代数学家祖暅提出的祖暅原理:“幂势既同,则积不容异”(“幂”是截面积,“势”是几何体的高),意思是两个同高的几何体,如在等高处截面的面积恒相等,则它们的体积相等.已知某不规则几何体与三视图(如图所示)所表示的几何体满足“幂势既同”,则该不规则几何体的体积为( )| A. | 8-2π | B. | 8-π | C. | $4-\frac{π}{2}$ | D. | $8-\frac{4π}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com