
ΓΨΧβΡΩΓΩ“―÷Σœ¬Ν–ΟϋΧβΘΚ
ΔΌΟϋΧβΓΑ ![]() Θ§
Θ§ ![]() Γ±ΒΡΖώΕ® «ΘΚΓΑ
Γ±ΒΡΖώΕ® «ΘΚΓΑ ![]() Θ§
Θ§ ![]() Γ±ΘΜ
Γ±ΘΜ
ΔΎ»τ―υ±Ψ ΐΨί ![]() ΒΡΤΫΨυ÷ΒΚΆΖΫ≤νΖ÷±πΈΣ
ΒΡΤΫΨυ÷ΒΚΆΖΫ≤νΖ÷±πΈΣ ![]() ΚΆ
ΚΆ ![]() ‘ρ ΐΨί
‘ρ ΐΨί ![]() ΒΡΤΫΨυ÷ΒΚΆ±ξΉΦ≤νΖ÷±πΈΣ
ΒΡΤΫΨυ÷ΒΚΆ±ξΉΦ≤νΖ÷±πΈΣ ![]() Θ§
Θ§ ![]() ΘΜ
ΘΜ
ΔέΝΫΗω ¬Φΰ≤Μ «ΜΞ≥β ¬ΦΰΒΡ±Ί“Σ≤Μ≥δΖ÷ΧθΦΰ «ΝΫΗω ¬Φΰ≤Μ «Ε‘ΝΔ ¬ΦΰΘΜ
Δή‘Ύ ![]() Ν–ΝΣ±μ÷–Θ§»τ±»÷Β
Ν–ΝΣ±μ÷–Θ§»τ±»÷Β ![]() ”κ
”κ ![]() œύ≤ν‘Ϋ¥σΘ§‘ρΝΫΗωΖ÷άύ±δΝΩ”–ΙΊœΒΒΡΩ…Ρή–‘ΨΆ‘Ϋ¥σΘ°
œύ≤ν‘Ϋ¥σΘ§‘ρΝΫΗωΖ÷άύ±δΝΩ”–ΙΊœΒΒΡΩ…Ρή–‘ΨΆ‘Ϋ¥σΘ°
Δί“―÷Σ ![]() ΈΣΝΫΗωΤΫΟφΘ§«“
ΈΣΝΫΗωΤΫΟφΘ§«“ ![]() Θ§
Θ§ ![]() ΈΣ÷±œΏΘ°‘ρΟϋΧβ:ΓΑ»τ
ΈΣ÷±œΏΘ°‘ρΟϋΧβ:ΓΑ»τ ![]() Θ§‘ρ
Θ§‘ρ ![]() Γ±ΒΡΡφΟϋΧβΚΆΖώΟϋΧβΨυΈΣΦΌΟϋΧβΘ°
Γ±ΒΡΡφΟϋΧβΚΆΖώΟϋΧβΨυΈΣΦΌΟϋΧβΘ°
Δό…ηΕ®Βψ ![]() ΓΔ
ΓΔ ![]() Θ§Ε·Βψ
Θ§Ε·Βψ ![]() ¬ζΉψΧθΦΰ
¬ζΉψΧθΦΰ ![]() ΈΣ’ΐ≥Θ ΐΘ©Θ§‘ρ
ΈΣ’ΐ≥Θ ΐΘ©Θ§‘ρ ![]() ΒΡΙλΦΘ «Ά÷‘≤Θ°Τδ÷–’φΟϋΧβΒΡΗω ΐΈΣ( )
ΒΡΙλΦΘ «Ά÷‘≤Θ°Τδ÷–’φΟϋΧβΒΡΗω ΐΈΣ( )
A.5
B.4
C.3
D.2
ΓΨ¥πΑΗΓΩA
ΓΨΫβΈωΓΩΔΌΟϋΧβΓΑ ![]() Θ§
Θ§ ![]() Γ±ΒΡΖώΕ® «ΘΚΓΑ
Γ±ΒΡΖώΕ® «ΘΚΓΑ ![]() Θ§
Θ§ ![]() Γ±,ΟϋΧβ’ΐ»Ζ;
Γ±,ΟϋΧβ’ΐ»Ζ;
ΔΎ ΐΨί ![]() ΒΡ±ξΉΦ≤ν
ΒΡ±ξΉΦ≤ν ![]() Θ§ΤΫΨυ ΐΈΣΘΚ
Θ§ΤΫΨυ ΐΈΣΘΚ ![]() Θ§ΟϋΧβ’ΐ»ΖΘΜ
Θ§ΟϋΧβ’ΐ»ΖΘΜ
ΔέΤδΡφΖώΟϋΧβ «ΘΚΝΫ ¬Φΰ «Ε‘ΝΔ ¬ΦΰΒΡ±Ί“Σ≤Μ≥δΖ÷ΧθΦΰ «ΝΫΗω ¬Φΰ «ΜΞ≥β ¬Φΰ.ΟϋΧβ’ΐ»ΖΘΜ
Δή ![]() ©¹
©¹ ![]() =
= ![]() Θ§ΓΏad©¹bcœύ≤ν‘Ϋ¥σΘ§ΝΫΗωΖ÷άύ±δΝΩ”–ΙΊœΒΒΡΩ…Ρή–‘ΨΆ‘Ϋ¥σΘ§
Θ§ΓΏad©¹bcœύ≤ν‘Ϋ¥σΘ§ΝΫΗωΖ÷άύ±δΝΩ”–ΙΊœΒΒΡΩ…Ρή–‘ΨΆ‘Ϋ¥σΘ§
Γύ ![]() ©¹
©¹ ![]() =œύ≤ν‘Ϋ¥σΘ§ΝΫΗωΖ÷άύ±δΝΩ”–ΙΊœΒΒΡΩ…Ρή–‘ΨΆ‘Ϋ¥σΘ§ΟϋΧβ’ΐ»ΖΘΜ
=œύ≤ν‘Ϋ¥σΘ§ΝΫΗωΖ÷άύ±δΝΩ”–ΙΊœΒΒΡΩ…Ρή–‘ΨΆ‘Ϋ¥σΘ§ΟϋΧβ’ΐ»ΖΘΜ
ΔίΡφΟϋΧβΘΚ“―÷Σ ![]() ΈΣΝΫΗωΤΫΟφΘ§«“
ΈΣΝΫΗωΤΫΟφΘ§«“ ![]() Θ§
Θ§ ![]() ΈΣ÷±œΏΘ°‘ρΟϋΧβ:ΓΑ»τ
ΈΣ÷±œΏΘ°‘ρΟϋΧβ:ΓΑ»τ ![]() Θ§‘ρ
Θ§‘ρ ![]() Γ±œ‘»Μl”κΤΫΟφ
Γ±œ‘»Μl”κΤΫΟφ ![]() ΙΊœΒ≤Μ»ΖΕ®Θ§Υυ“‘ΡφΟϋΧβΈΣΦΌΟϋΧβΘ§ΡφΟϋΧβ”κΖώΟϋΧβΆ§’φΆ§ΦΌΘ§Ι Εΰ’ΏΆ§ΈΣΦΌΟϋΧβ;
ΙΊœΒ≤Μ»ΖΕ®Θ§Υυ“‘ΡφΟϋΧβΈΣΦΌΟϋΧβΘ§ΡφΟϋΧβ”κΖώΟϋΧβΆ§’φΆ§ΦΌΘ§Ι Εΰ’ΏΆ§ΈΣΦΌΟϋΧβ;
ΔόΒ± ![]() ±Θ§
±Θ§ ![]() ΒΡΙλΦΘ «œΏΕΈΘ§œ‘»ΜΟϋΧβ «ΦΌΟϋΧβΘΜ
ΒΡΙλΦΘ «œΏΕΈΘ§œ‘»ΜΟϋΧβ «ΦΌΟϋΧβΘΜ
Υυ“‘’φΟϋΧβΗω ΐΈΣ5Ηω
Ι ¥πΑΗΈΣΘΚA
ΗυΨίΧβ“β”…ΧΊ≥ΤΟϋΧβΚΆ»Ϊ≥ΤΟϋΧβΓΔΤΫΨυ ΐ”κ±ξΉΦΖΫ≤νΒΡ‘ΥΥψΓΔΕ‘ΝΔ ¬Φΰ”κΜΞ≥β ¬ΦΰΒΡΙΊœΒΓΔΕάΝΔ–‘Φλ―ιΓΔœΏΟφΈΜ÷ΟΙΊœΒΒΡ≈–ΕœΓΔΆ÷‘≤Ε®“εΒΡ‘Υ”ΟΘ§…ν»κ«≥≥ωΒΡΩΦ≤λΝΥΕ‘’β–©ΗωΜυ±Ψ÷Σ Ε”κΜυ±ΨΖΫΖ®ΒΡ‘Υ”ΟΓΘ



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§ ![]() ΈΣ‘≤÷υ
ΈΣ‘≤÷υ ![]() ΒΡΡΗœΏΘ§
ΒΡΡΗœΏΘ§ ![]() «ΒΉΟφ‘≤
«ΒΉΟφ‘≤ ![]() ΒΡ÷±ΨΕΘ§
ΒΡ÷±ΨΕΘ§ ![]() «
« ![]() ΒΡ÷–Βψ.
ΒΡ÷–Βψ.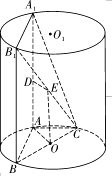
Θ®ΔώΘ©Έ ΘΚ ![]() …œ «Ζώ¥φ‘ΎΒψ
…œ «Ζώ¥φ‘ΎΒψ ![]() ΙΒΟ
ΙΒΟ ![]() ΤΫΟφ
ΤΫΟφ ![]() ΘΩ«κΥΒΟςάμ”…ΘΜ
ΘΩ«κΥΒΟςάμ”…ΘΜ
Θ®ΔρΘ©‘ΎΘ®ΔώΘ©ΒΡΧθΦΰœ¬Θ§»τ ![]() ΤΫΟφ
ΤΫΟφ ![]() Θ§ΦΌ…η’βΗω‘≤÷υ «“ΜΗω¥σ»ίΤςΘ§”–ΧθΧεΜΐΩ…“‘Κω¬‘≤ΜΦΤΒΡ–Γ”ψΡή‘Ύ»ίΤςΒΡ»Έ“βΒΊΖΫ”ΈΏ°Θ§»γΙϊ–Γ”ψ”ΈΒΫΥΡάβΉΕ
Θ§ΦΌ…η’βΗω‘≤÷υ «“ΜΗω¥σ»ίΤςΘ§”–ΧθΧεΜΐΩ…“‘Κω¬‘≤ΜΦΤΒΡ–Γ”ψΡή‘Ύ»ίΤςΒΡ»Έ“βΒΊΖΫ”ΈΏ°Θ§»γΙϊ–Γ”ψ”ΈΒΫΥΡάβΉΕ ![]() ΆβΜα”–±Μ≤ΕΒΡΈΘœ’Θ§«σ–Γ”ψ±Μ≤ΕΒΡΗ≈¬ .
ΆβΜα”–±Μ≤ΕΒΡΈΘœ’Θ§«σ–Γ”ψ±Μ≤ΕΒΡΗ≈¬ .
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΕ‘”ΎΆ÷‘≤ ![]() Θ§”–»γœ¬–‘÷ ΘΚ»τΒψ
Θ§”–»γœ¬–‘÷ ΘΚ»τΒψ ![]() «Ά÷‘≤…œΒΡΒψΘ§‘ρΆ÷‘≤‘ΎΗΟΒψ¥ΠΒΡ«–œΏΖΫ≥ΧΈΣ
«Ά÷‘≤…œΒΡΒψΘ§‘ρΆ÷‘≤‘ΎΗΟΒψ¥ΠΒΡ«–œΏΖΫ≥ΧΈΣ ![]() .άϊ”Ο¥ΥΫα¬έΫβ¥πœ¬Ν–Έ Χβ.
.άϊ”Ο¥ΥΫα¬έΫβ¥πœ¬Ν–Έ Χβ.
Θ®ΔώΘ©«σΆ÷‘≤ ![]() ΒΡ±ξΉΦΖΫ≥ΧΘΜ
ΒΡ±ξΉΦΖΫ≥ΧΘΜ
Θ®ΔρΘ©»τΕ·Βψ ![]() ‘Ύ÷±œΏ
‘Ύ÷±œΏ ![]() …œΘ§Ψ≠ΙΐΒψ
…œΘ§Ψ≠ΙΐΒψ ![]() ΒΡ÷±œΏ
ΒΡ÷±œΏ ![]() ”κΆ÷‘≤
”κΆ÷‘≤ ![]() œύ«–Θ§«–ΒψΖ÷±πΈΣ
œύ«–Θ§«–ΒψΖ÷±πΈΣ ![]() .«σ÷Λ÷±œΏ
.«σ÷Λ÷±œΏ ![]() ±ΊΨ≠Ιΐ“ΜΕ®Βψ.
±ΊΨ≠Ιΐ“ΜΕ®Βψ.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ…ηxΘ§y¬ζΉψ≤ΜΒ» ΫΉι  Θ§»τz=ax+yΒΡΉν¥σ÷ΒΈΣ2a+4Θ§Ήν–Γ÷ΒΈΣa+1Θ§‘ρ Β ΐaΒΡ»Γ÷ΒΖΕΈßΈΣ Θ°
Θ§»τz=ax+yΒΡΉν¥σ÷ΒΈΣ2a+4Θ§Ήν–Γ÷ΒΈΣa+1Θ§‘ρ Β ΐaΒΡ»Γ÷ΒΖΕΈßΈΣ Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ―Γ–ό4-4ΘΚΉχ±ξœΒ”κ≤Έ ΐΖΫ≥Χ
‘Ύ÷±Ϋ«Ήχ±ξœΒ ![]() ÷–Θ§÷±œΏ
÷–Θ§÷±œΏ ![]() Ιΐ
Ιΐ ![]() Θ§«ψ–±Ϋ«ΈΣ
Θ§«ψ–±Ϋ«ΈΣ ![]() Θ°“‘
Θ°“‘ ![]() ΈΣΦΪΒψΘ§
ΈΣΦΪΒψΘ§ ![]() ÷αΖ«ΗΚΑκ÷αΈΣΦΪ÷αΘ§Ϋ®ΝΔΦΪΉχ±ξœΒΘ§«ζœΏ
÷αΖ«ΗΚΑκ÷αΈΣΦΪ÷αΘ§Ϋ®ΝΔΦΪΉχ±ξœΒΘ§«ζœΏ ![]() ΒΡΦΪΉχ±ξΖΫ≥ΧΈΣ
ΒΡΦΪΉχ±ξΖΫ≥ΧΈΣ ![]() Θ°
Θ°
Θ®ΔώΘ©«σ÷±œΏ ![]() ΒΡ≤Έ ΐΖΫ≥ΧΚΆ«ζœΏ
ΒΡ≤Έ ΐΖΫ≥ΧΚΆ«ζœΏ ![]() ΒΡ÷±Ϋ«Ήχ±ξΖΫ≥ΧΘΜ
ΒΡ÷±Ϋ«Ήχ±ξΖΫ≥ΧΘΜ
Θ®ΔρΘ©“―÷Σ÷±œΏ ![]() ”κ«ζœΏ
”κ«ζœΏ ![]() ΫΜ”Ύ
ΫΜ”Ύ ![]() ΓΔ
ΓΔ ![]() ΝΫΒψΘ§«“
ΝΫΒψΘ§«“ ![]() Θ§«σ÷±œΏ
Θ§«σ÷±œΏ ![]() ΒΡ–±¬
ΒΡ–±¬ ![]() Θ°
Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΆ÷‘≤ ![]() ΒΡάκ–Ρ¬ ΈΣ
ΒΡάκ–Ρ¬ ΈΣ ![]() Θ§«“Ά÷‘≤
Θ§«“Ά÷‘≤ ![]() ΙΐΒψ
ΙΐΒψ ![]() Θ§÷±œΏ
Θ§÷±œΏ ![]() ΙΐΆ÷‘≤
ΙΐΆ÷‘≤ ![]() ΒΡ”“ΫΙΒψ
ΒΡ”“ΫΙΒψ ![]() «“”κΆ÷‘≤
«“”κΆ÷‘≤ ![]() ΫΜ”Ύ
ΫΜ”Ύ ![]() ΝΫΒψ.
ΝΫΒψ.
(Δώ)«σΆ÷‘≤ ![]() ΒΡ±ξΉΦΖΫ≥ΧΘΜ
ΒΡ±ξΉΦΖΫ≥ΧΘΜ
(Δρ)“―÷ΣΒψ ![]() Θ§«σ÷ΛΘΚ»τ‘≤
Θ§«σ÷ΛΘΚ»τ‘≤ ![]() ”κ÷±œΏ
”κ÷±œΏ ![]() œύ«–Θ§‘ρ‘≤
œύ«–Θ§‘ρ‘≤ ![]() ”κ÷±œΏ
”κ÷±œΏ ![]() “≤œύ«–.
“≤œύ«–.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ÷¥––»γΆΦΥυ ΨΒΡ≥Χ–ρΩρΆΦΘ§»τ δ≥ωΒΡ ![]() ÷ΒΈΣ11Θ§‘ρ≈–ΕœΩρ÷–ΒΡΧθΦΰΩ…“‘ «Θ® Θ©
÷ΒΈΣ11Θ§‘ρ≈–ΕœΩρ÷–ΒΡΧθΦΰΩ…“‘ «Θ® Θ©![]()
A.![]()
B.![]()
C.![]()
D.![]()
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐf(x)ΘΫexΘ≠eΘ≠x(xΓ RΘ§«“eΈΣΉ‘»ΜΕ‘ ΐΒΡΒΉ ΐ).
Θ®1Θ©≈–ΕœΚ· ΐf(x)ΒΡΒΞΒς–‘”κΤφ≈Φ–‘ΘΜ
Θ®2Θ© «Ζώ¥φ‘Ύ Β ΐt Θ§ Ι≤ΜΒ» Ϋf(xΘ≠t)ΘΪf(x2Θ≠t2)Γί0Ε‘“Μ«–xΓ RΕΦ≥…ΝΔΘΩ»τ¥φ‘ΎΘ§«σ≥ωtΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”….
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐ![]() .
.
Θ®1Θ©Χ÷¬έΚ· ΐ![]() ΒΡΒΞΒς–‘ΘΜ
ΒΡΒΞΒς–‘ΘΜ
Θ®2Θ©«σ![]() ‘Ύ
‘Ύ![]() …œΒΡΉν¥σ÷ΒΚΆΉν–Γ÷Β.
…œΒΡΉν¥σ÷ΒΚΆΉν–Γ÷Β.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com