
2007年杭州市第一次高考科目教学质量检测
数学试题卷(文科)
考生须知:
1. 本卷满分150分, 考试时间120分钟.
2. 答题前, 在答题卷密封区内填写学校、班级和姓名.
3. 所有答案必须写在答题卷上, 写在试题卷上无效.
4. 考试结束, 只需上交答题卷.
参考公式
如果事件 互斥,那么
互斥,那么 ;
;
如果事件 相互独立,那么
相互独立,那么 ;
;
如果事件 在一次试验中发生的概率是
在一次试验中发生的概率是 ,那么
,那么 次独立重复试验中恰好发生
次独立重复试验中恰好发生 次的概率
次的概率 .
.
一. 选择题 : 本大题共10小题, 每小题5分, 共50分. 在每小题给出的四个选项中, 只有一项是符合题目要求的 .
1. 以下4组函数中, 表示同一函数的是 ( )
(A)  (B)
(B)

 2.
某校为了了解学生的课外阅读情况,随
2.
某校为了了解学生的课外阅读情况,随
机调查了50名学生,得到他们在某一天各
自课外阅读所用时间的数据,结果用右侧
的条形图表示. 根据条形图可得这50名学
生这一天平均每人的课外阅读时间为 ( )
(第2题)
(A) 0.6小时 (B) 0.9小时
(C) 1.0小时 (D) 1.5小时
3. 记函数 的反函数为
的反函数为 ,则
,则 ( )
( )
(A) 2 (B) -2 (C) 3 (D) -3
4. 设数列 是等差数列, 且
是等差数列, 且 是数列
是数列 的前
的前 项的和, 则有
项的和, 则有
( )
(A)  (B)
(B)  (C)
(C)  (D)
(D) 
5. 已知 , 则
, 则 的最小值为 ( )
的最小值为 ( )
(A) 6 (B) 7 (C) 8 (D) 9
6. 已知| a | = 3,
| b | = 4,
(a +
b)?( a +3 b) = 33, 则a与b的夹角 为 ( )
为 ( )
(A)  (B)
(B)
 (C)
(C)
 (D)
(D)

7. 给出四个函数分别满足: ①  ; ②
; ②  ;
;
③  ; ④
; ④  . 与下列函数图象相对应的是
. 与下列函数图象相对应的是
( )


(第7题)
(A) ① ②
② ③
③ ④
④ (B) ①
(B) ① ②
② ③
③ ④
④
(C) ① ②
② ③
③ ④
④ (D) ①
(D) ① ②
② ③
③ ④
④
8. 设两个独立事件 都不发生的概率为
都不发生的概率为 ,
,  发生
发生 不发生的概率与
不发生的概率与 发生
发生 不发生的概率相等, 那么
不发生的概率相等, 那么 为 ( )
为 ( )
(A)  (B)
(B)
 (C)
(C)  (D)
(D)

9.已知曲线 ,则过点
,则过点 的切线方程是 ( )
的切线方程是 ( )
(A)  (B)
(B) 
(C)  (D)
(D) 
10.
定义在R上的偶函数 满足
满足 ,当
,当 ∈[3,4]时,
∈[3,4]时, ,则有 ( )
,则有 ( )
(C)  (D)
(D)

二.填空题: 本大题有4小题, 每小题4分, 共16分. 把答案填在答题卷的相应位置.
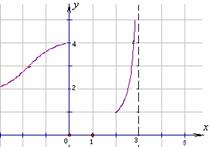
(第11题)
11. 函数 的图象如右所示.
的图象如右所示.
那么,  的定义域是 ________ ; 值域是
的定义域是 ________ ; 值域是
__________ ; 其中只与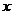 的一个值对应的
的一个值对应的 值的范围是 ________________ .
值的范围是 ________________ .
12. 已知角 的终边在直线
的终边在直线 上,
上,
则 的值是 __________ .
的值是 __________ .
13. 一个总体中有100个个体,随机编号0,1,2,…,99,依编号顺序平均分成10个
小组,组号依次为1,2,3,…,10. 现用系统抽样方法抽取一个容量为10的样本,规
定如果在第1组随机抽取的号码为 ,那么在第
,那么在第 组中抽取的号码个位数字与
组中抽取的号码个位数字与 的
的
个位数字相同,若 ,则在第7组中抽取的号码是
.
,则在第7组中抽取的号码是
.
14. 一个不懂英语的小孩用写有
“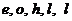 ” 5个英语字母的卡片拼成单词“
” 5个英语字母的卡片拼成单词“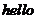 ”, 那么可能是错误的拼法(卡片不横放也不颠倒)共有 _____ 种.
”, 那么可能是错误的拼法(卡片不横放也不颠倒)共有 _____ 种.
三. 解答题: 本大题有6小题, 每小题14分,共84分. 解答应写出文字说明, 证明过程或演算步骤.
15. (本小题满分14分)
已知集合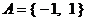 ,
, 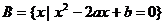 , 若
, 若 且
且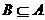 , 求
, 求
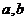 的值.
的值.
16. (本小题满分14分)
设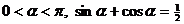 , 求
, 求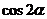 的值.
的值.
17.(本小题满分14分)
已知数列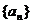 的前
的前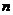 项和
项和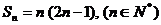 .
.
(1)
求数列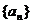 的通项公式,并证明该数列为等差数列;
的通项公式,并证明该数列为等差数列;
(2)
设数列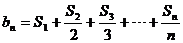
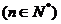 , 试判定: 是否存在自然数
, 试判定: 是否存在自然数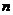 ,
,
使得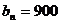 ,若存在, 求出
,若存在, 求出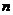 的值;若不存在,说明理由.
的值;若不存在,说明理由.
18 . (本小题满分14分)
已知函数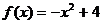 ,设函数
,设函数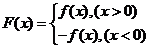 .
.
(1)求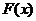 表达式;
表达式;
(2)解不等式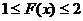 ;
;
(3)设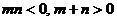 , 判断
, 判断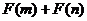 能否小于0 ?
能否小于0 ?
19. (本小题满分14分)
杭州风景区有一家自行车租车公司,公司设有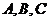 三个营业站,顾客可以从任何一处营业站租车,并在任何一处营业站还车. 根据统计发现租车处与还车处有如下的规律性:
三个营业站,顾客可以从任何一处营业站租车,并在任何一处营业站还车. 根据统计发现租车处与还车处有如下的规律性:
1) 在 站租车者有30%在
站租车者有30%在 站还车,20%在
站还车,20%在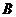 站还车,50%在
站还车,50%在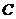 站还车;
站还车;
2) 在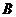 站租车者有70%在
站租车者有70%在 站还车,10%在
站还车,10%在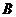 站还车,20%在
站还车,20%在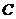 站还车;
站还车;
记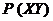 表示 “某车由
表示 “某车由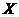 站租出还至
站租出还至 站的概率”,
站的概率”, 表示 “某车由
表示 “某车由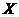 站租出还至
站租出还至 站, 再由
站, 再由 站还至
站还至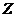 站的概率”. 按以上约定的规则,
站的概率”. 按以上约定的规则,
(1) 求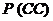 ;
;
(2) 求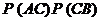 ;
;
(3) 设某辆自行车从 站租出,求此车归还至某站再次出租后,回到
站租出,求此车归还至某站再次出租后,回到 站的概率
站的概率 .
.
20. (本小题满分14分)
设函数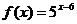 ,
, 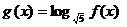
(1)
解不等式
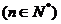 ;
;
(2)
求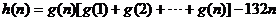
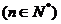 的最小值.
的最小值.
2007年杭州市第一次高考科目教学质量检测
数学参考评分标准(文科)
一. 选择题 : (本大题共10小题, 每小题5分, 共50分)
题号
1
2
3
4
5
6
7
8
9
10
答案
A
B
B
A
D
D
B
A
C
二.填空题: (本大题有4小题, 每小题4分, 共16分)
11. 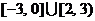 ; [1,5];
; [1,5];  . (端点相对应为开也可, 左, 上为无穷也可)
. (端点相对应为开也可, 左, 上为无穷也可)
12.  或
或 13. 63 14.
59
13. 63 14.
59
三. 解答题: (本大题有6小题, 每小题14分,共84分)
15. (本小题满分14分)
因为 , 且
, 且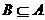 , 所以
, 所以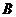 有两种存在情况:
有两种存在情况:
(1) 当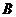 含有两个元素时,
含有两个元素时, 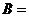
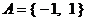 , 易得
, 易得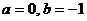 ;
--- 4分
;
--- 4分
(2) 当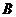 含有一个元素时, 由
含有一个元素时, 由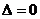 , 得
, 得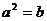 ,
--- 2分
,
--- 2分
若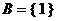 时, 由
时, 由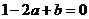 , 得
, 得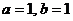 ;
---
4分
;
---
4分
若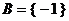 时, 由
时, 由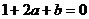 , 得
, 得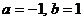 .
--- 4分
.
--- 4分
16. (本小题满分14分)
由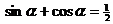 , 可得
, 可得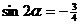 --- 5分
--- 5分
但由条件又知应该有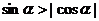 , 即
, 即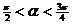 , ∴
, ∴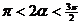 ,
--- 4分
,
--- 4分
∴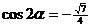 .
--- 5分
.
--- 5分
17.(本小题满分14分)
(1)
当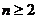 时,
时,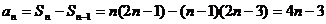 ,
--- 4分
,
--- 4分
当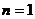 时,
时, 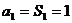 , 适合, ∴
, 适合, ∴ 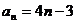 ,
--- 2分
,
--- 2分
而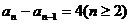 ,所以
,所以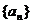 为等差数列.
--- 2分
为等差数列.
--- 2分
(2)
∵ 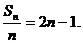 , ---
2分
, ---
2分
∴ 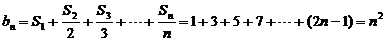 ,
--- 2分
,
--- 2分
由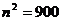 , 得
, 得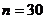 , 即存在满足条件的自然数为30.
--- 2分
, 即存在满足条件的自然数为30.
--- 2分
18 . (本小题满分14分)
(1) 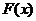 =
= 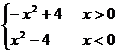 ;
--- 2分
;
--- 2分
当 时, 解不等式 1 £
时, 解不等式 1 £ 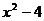 £ 2, 得 ?
£ 2, 得 ?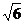 £
£ 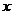 £ ?
£ ?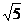 .
--- 2分
.
--- 2分
综合上述不等式的解为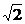 £
£ 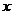 £
£ 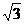 或?
或?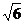 £
£ 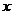 £ ?
£ ?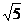 .
--- 2分
.
--- 2分
(3)∵ 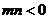 , 不妨设
, 不妨设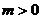 , 则
, 则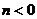 , 又
, 又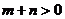 , ∴
, ∴ 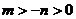 ,
,
∴  , ---
2分
, ---
2分
∴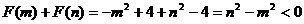 ,
,
即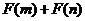 能小于0.
--- 4分
能小于0.
--- 4分
19.(本小题满分14分)
(1) 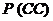 = 0.1;
---
4分
= 0.1;
---
4分
(2)  ;
--- 4分
;
--- 4分
(3) 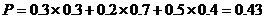 .
--- 6分
.
--- 6分
20. (本小题满分14分)
(1)  ,
--- 2分
,
--- 2分
∴  ,
--- 2分
,
--- 2分
解不等式 , 得
, 得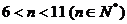 ;
--- 2分
;
--- 2分
(2) 当 时,
时,  ,
,
--- 2分
∵  , ∴
, ∴  时,
时,  单调递减,
单调递减, 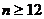 时,
时,  单调递增, --- 2分
单调递增, --- 2分
当 时,
时, 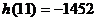 , 当
, 当 时,
时, 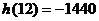 ,
,
∴  .
---
2分
.
---
2分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com