
2009年江苏省高考数学重点内容分类精析
一.集合(集合及其表示A;子集B,交集、并集、补集B)
1.
满足 ,且
,且
 的集合
的集合 的个数是 2
的个数是 2
2.
设 是一个数集,且至少含有两个数,若对任意
是一个数集,且至少含有两个数,若对任意 都有
都有 (除数
(除数 ),则称P是一个数域,例如有理数Q是数域。有下列命题:①数域必含有0,1两个数;②整数集是数域;③若有理数
),则称P是一个数域,例如有理数Q是数域。有下列命题:①数域必含有0,1两个数;②整数集是数域;③若有理数 ,则数集
,则数集 必为数域;④数域必为无限集。
必为数域;④数域必为无限集。
其正确的命题的序号是 ①④ (把你认为正确的命题的序号都填上)
二.函数概念与基本初等函数Ⅰ(函数的概念B;函数的基本性质B)
3.
若函数 的定义域是
的定义域是 ,则函数
,则函数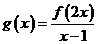 的定义域是 [0,1]
的定义域是 [0,1]
4.
定义在R上的函数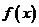 满足
满足 ,
, ,则
,则 等于
等于
6
5.
设函数 ,则
,则 的值为
的值为
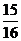
三.函数概念与基本初等函数Ⅰ(指数与对数B;指数与对数的图象和性质B;对数函数的图象和性质B;幂函数A;函数与方程A;函数模型及其应用B))
6.则下列四个结论正确的是 ③ (填正确序号)
①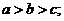 ②
②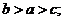 ③
③ ; ④
; ④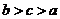
7.已知函数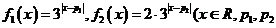 为常当选),函数
为常当选),函数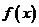 的定义为:对每一个给定的实数
的定义为:对每一个给定的实数 ,
,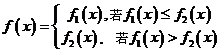
(1)
求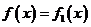 对所有实数
对所有实数 成立的充分必要条件(用
成立的充分必要条件(用 表示)
表示)
(2)
设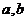 是两个实数,满足
是两个实数,满足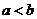 且
且 ,若
,若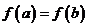 ,求证:函数
,求证:函数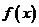 在区间
在区间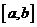 上的单调增区间的长度之和为
上的单调增区间的长度之和为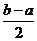 (闭区间
(闭区间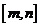 的长度定义为
的长度定义为 )
)
解:(1)由 的定义可知,
的定义可知, (对所有实数
(对所有实数 )等价于
)等价于
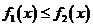 (对所有实数
(对所有实数 )这又等价于
)这又等价于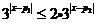 ,即
,即
 对所有实数
对所有实数 均成立. (*)
均成立. (*)
由于 的最大值为
的最大值为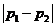 ,
,
故(*)等价于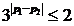 ,即
,即 ,这就是所求的充分必要条件
,这就是所求的充分必要条件
(2)分两种情形讨论
(i)当 时,由(1)知
时,由(1)知 (对所有实数
(对所有实数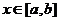 )
)
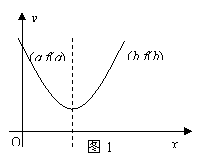 则由
则由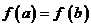 及
及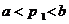 易知
易知 ,
,
再由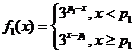 的单调性可知,
的单调性可知,
函数 在区间
在区间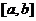 上的单调增区间的长度
上的单调增区间的长度
为 (参见示意图1)
(参见示意图1)
(ii)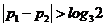 时,不妨设
时,不妨设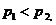 ,则
,则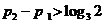 ,于是
,于是
当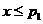 时,有
时,有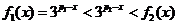 ,从而
,从而 ;
;
当 时,有
时,有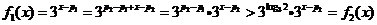
从而  ;
;
当 时,
时,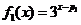 ,及
,及 ,由方程
,由方程
 解得
解得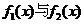 图象交点的横坐标为
图象交点的横坐标为
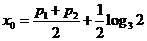 ⑴
⑴
显然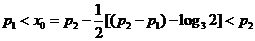 ,
,
这表明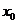 在
在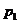 与
与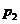 之间。由⑴易知
之间。由⑴易知

综上可知,在区间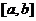 上,
上,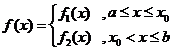 (参见示意图2)
(参见示意图2)
故由函数 及
及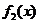 的单调性可知,
的单调性可知, 在区间
在区间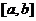 上的单调增区间的长度之和为
上的单调增区间的长度之和为 ,由于
,由于 ,即
,即 ,得
,得
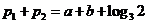 ⑵
⑵
故由⑴、⑵得 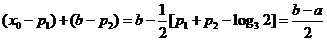
综合(i)(ii)可知, 在区间
在区间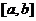 上的单调增区间的长度和为
上的单调增区间的长度和为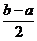 。
。
8.
已知二次函数
(1)
若函数在区间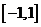 上存在零点,求实数
上存在零点,求实数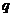 的取值范围;
的取值范围;
(2)
问:是否存在常数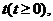 当
当 时,
时,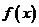 的值域为区间D,且D的长度为
的值域为区间D,且D的长度为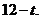
9.水库的蓄水量随时间而变化,现用 表示时间,以月为单位,年初为起点,根据历年数据,某水库的蓄水量(单位:亿立方米)关于
表示时间,以月为单位,年初为起点,根据历年数据,某水库的蓄水量(单位:亿立方米)关于 的近似函数关系式为
的近似函数关系式为

(Ⅰ)该水库的蓄求量小于50的时期称为枯水期.以 表示第1月份(
表示第1月份(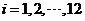 ),问一年内哪几个月份是枯水期?
),问一年内哪几个月份是枯水期?
(Ⅱ)求一年内该水库的最大蓄水量(取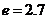 计算).
计算).
解:本小题主要考查函数、导数和不等式等基本知识,考查用导数求最值和综合运用数学知识解决实际问题能力.
(Ⅰ)①当 时,
时, ,化简得
,化简得 ,
,
解得 ,或
,或 ,又
,又 ,故
,故 .
.
②当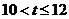 时,
时,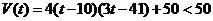 ,化简得
,化简得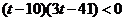 ,
,
解得 ,又
,又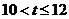 ,故
,故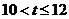 .
.
综合得 ,或
,或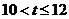 ;
;
故知枯水期为1月,2月,3月,11月,12月共5个月.
(Ⅱ)(Ⅰ)知:V(t)的最大值只能在(4,10)内达到.
由V′(t)=

令V′(t)=0,解得t=8(t=-2舍去).
当t变化时,V′(t) 与V (t)的变化情况如下表:
t
(4,8)
8
(8,10)
V′(t)
+
0
-
V(t)

极大值

由上表,V(t)在t=8时取得最大值V(8)=8e2+50-108.52(亿立方米).
故知一年内该水库的最大蓄水量是108.32亿立方米
四.函数概念与基本初等函数Ⅱ(三角函数的有关概念B;同角三角函数的基本关系式B;正弦、余弦的诱导公式B;正弦函数、余弦函数、正切函数的图象和性质B;函数 的图象和性质A;两角和(差)的正弦、余弦、和正切C;二倍角的正弦、余弦和正切B;积化和差、和差化积、半角公式A)
的图象和性质A;两角和(差)的正弦、余弦、和正切C;二倍角的正弦、余弦和正切B;积化和差、和差化积、半角公式A)
10.函数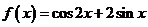 的最小值和最大值分别为
的最小值和最大值分别为 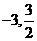
11.已知函数 (
( ,
,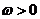 )为偶函数,且函数
)为偶函数,且函数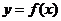 图象的两相邻对称轴间的距离为
图象的两相邻对称轴间的距离为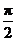 .
.
(Ⅰ)求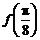 的值;
的值;
(Ⅱ)将函数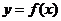 的图象向右平移
的图象向右平移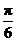 个单位后,再将得到的图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数
个单位后,再将得到的图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数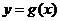 的图象,求
的图象,求 的单调递减区间.
的单调递减区间.
解:(Ⅰ)
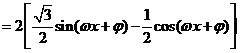
 .
.
因为 为偶函数,所以对
为偶函数,所以对 ,
,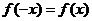 恒成立,
恒成立,
因此 .
.
即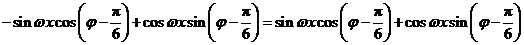 ,
,
整理得 .因为
.因为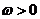 ,且
,且 ,所以
,所以 .
.
又因为 ,故
,故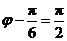 .所以
.所以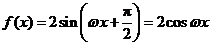 .
.
由题意得 ,所以
,所以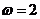 .故
.故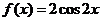 .因此
.因此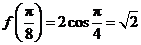 .
.
(Ⅱ)将 的图象向右平移
的图象向右平移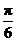 个单位后,得到
个单位后,得到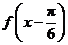 的图象,
的图象,
所以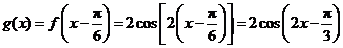 .
.
当 (
(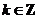 ),
),
即 (
(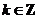 )时,
)时, 单调递减,
单调递减,
因此 的单调递减区间为
的单调递减区间为 (
(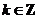 ).
).
 12.如图,某地有三家工厂,分别位于矩形ABCD的两个顶点A,B及CD的中点P处.AB=
12.如图,某地有三家工厂,分别位于矩形ABCD的两个顶点A,B及CD的中点P处.AB=
(1)按下列要求建立函数关系式:
(Ⅰ)设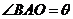 (rad),将
(rad),将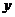 表示成
表示成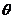 的函数;
的函数;
(Ⅱ)设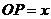 (km),将
(km),将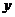 表示成
表示成 的函数;
的函数;
(3) 请你选用(1)中的一个函数关系确定污水处理厂的位置,使铺设的污水管道的总长度最短。
函数概念与基本初等函数Ⅱ(两角和(差)的正弦、余弦和正切;二倍角的正弦、余弦和正切;几个三角不等式)
解:(Ⅰ)①由条件知PQ 垂直平分AB,若∠BAO=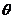 (rad) ,则
(rad) ,则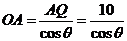 ,
,
故 ,又OP=
,又OP=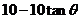 ,
,
所以 ,
,
所求函数关系式为
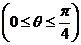
②若OP= (km) ,则OQ=10-
(km) ,则OQ=10- ,所以OA =OB=
,所以OA =OB=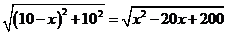
所求函数关系式为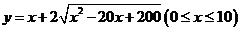
(Ⅱ)选择函数模型①,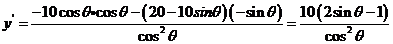
令 0 得sin
0 得sin  ,因为
,因为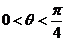 ,所以
,所以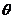 =
= ,
,
当 时,
时,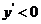 ,
,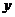 是
是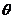 的减函数;
的减函数;
当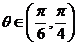 时,
时,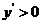 ,
,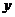 是
是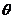 的增函数,所以当
的增函数,所以当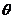 =
= 时,
时,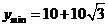 。
。
这时点P 位于线段AB 的中垂线上,在矩形区域内且距离AB 边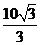 km处。
km处。
13.已知函数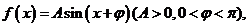
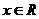 的最大值是1,其图象经过点M(
的最大值是1,其图象经过点M(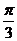 ,
,
(1)求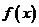 的解析式;(2)已知
的解析式;(2)已知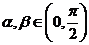 ,且
,且 ,求
,求 的值。
的值。
解析:(1)依题意有 ,则
,则 ,将点
,将点 代入得
代入得 ,
,
而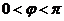 ,
,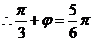 ,
,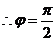 ,故
,故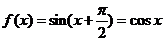 ;
;
(2)依题意有 ,而
,而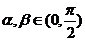 ,
,
 ,
,
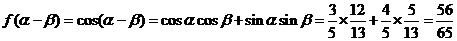 。
。
五.解三角形(正弦定理、余弦定理及其应用B)
14.满足条件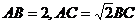 的三角形
的三角形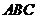 的面积的最大值
的面积的最大值
 15.
15.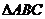 的三内角
的三内角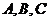 的对边边长分别为
的对边边长分别为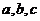 ,若
,若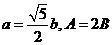 ,则
,则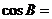
16.如图,△ACD是等边三角形,△ABC是等腰直角三角形,∠ACB=90°,BD交AC于E,AB=2。
(1)求cos∠CBE的值;(2)求AE。
解:(1) 因为
所以 ,
,
(2)在 中,
中,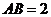 ,故由正弦定理得
,故由正弦定理得
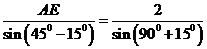 ,故
,故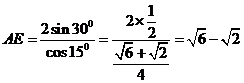
17.已知函数
 在
在 单调增加,在
单调增加,在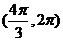 单调减少,则
单调减少,则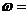
六.平面向量(平面向量的有关概念B;平面向量的加法、减法和数乘运算B;平面向量的坐标表示B;平面向量的数量积C;平面向量的平行与垂直B;平面向量的应用A)
18.已知四边形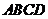 的三个顶点
的三个顶点 ,
, ,
,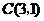 ,且
,且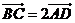 ,
,
则顶点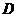 的坐标为
的坐标为 
19.已知平面向量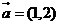 ,
,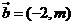 ,且
,且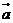 //
// ,则
,则 =
= 
20.已知 为
为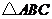 的三个内角
的三个内角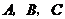 的对边,向量
的对边,向量
 .若
.若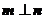 ,且
,且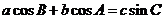 ,
,
则角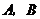 的大小分别为
的大小分别为 
21.设平面向量 ,若存在实数
,若存在实数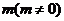 和角
和角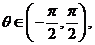 使向量
使向量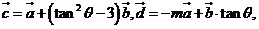 且
且
(1)求 的关系式;(2)若
的关系式;(2)若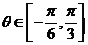 ,求
,求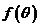 的最小值,并求出此时的
的最小值,并求出此时的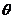 值。
值。
七.数列(数列的有关概念A;等差数列C;等比数列C)
22.将全体正整数排成一个三角形数阵:
|