
2009年云南省曲靖一中高考冲刺卷 文科数学(三)
文科数学(三)

本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分150分,考试时间120分钟.
第Ⅰ卷(选择题,共60分) 
一、选择题:本大题共12小题.每小题5分,共60分.在每小题给出的四个选项中.只
有一项是符合题目要求的.
1.设集合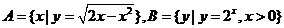 ,则
,则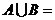

A.(1,2] B.[0,+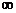 )
)
C.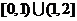 D.[0,2]
D.[0,2]
2.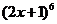 展开式中
展开式中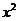 的系数为
的系数为
A.
3.若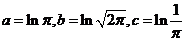 ,则
,则
A.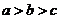 B.
B.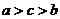 C.
C.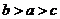 D.
D.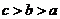

4.若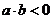 ,则
,则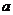 与
与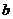 的夹角
的夹角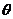 的取值范围是
的取值范围是
A.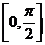 B.
B.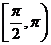 C.
C.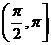 D.
D.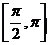

5.在等差数列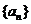 中,有
中,有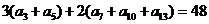 ,则此数列的前13项之和为
,则此数列的前13项之和为
A.24 B.39 C.52 D.104
6.曲线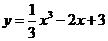 在点
在点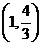 处的切线的倾斜角为
处的切线的倾斜角为
A.150° B.135° C.60° D.45°
7.函数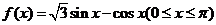 的最小值为
的最小值为
A.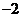 B.1 C.
B.1 C.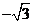 D.
D.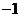

8.设偶函数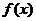 在
在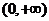 上为减函数,且
上为减函数,且 ,则不等式
,则不等式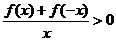 的解
的解
集为
A.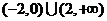 B.
B.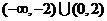

C. D.
D.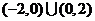

9.要得到函数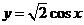 的图象,只需将函数
的图象,只需将函数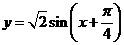 的图象
的图象
A.向左平移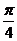 个长度单位 B.向右平移
个长度单位 B.向右平移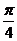 个长度单位
个长度单位
C.向左平移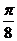 个长度单位 D.向右平移
个长度单位 D.向右平移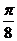 个长度单位
个长度单位
10.若直线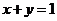 通过点
通过点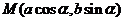 ,则
,则
A.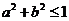 B.
B.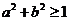

C.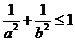 D.
D.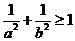

11.已知四棱柱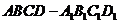 的底面为正方形,侧棱与底面边长相等,
的底面为正方形,侧棱与底面边长相等,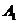 在底面
在底面
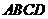 内的射影为正方形
内的射影为正方形 的中心,则
的中心,则 与底面
与底面 所成角的正弦值等于
所成角的正弦值等于
A.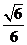 B.
B.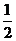 C.
C.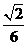 D.
D.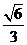

12.若以连续掷两骰子分别得到点数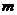 、
、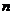 作为点
作为点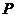 的坐标,则
的坐标,则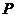 落在区域
落在区域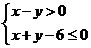

内的概率为
A.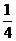 B.
B.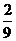 C.
C.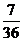 D.
D.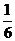


第Ⅱ卷(非选择题,共90分)
13.某校高一、高二、高三三个年级的学生数分别为1500人、1200人和1000人,现采用
按年级分层抽样法了解学生的视力状况,已知高一年级抽查了75人,则这次调查三个
年级共抽查了 人.
14.某市拟从4个重点项目和6个一般项目各选2个项目作为本年度要启动的项目,则重点
项目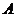 和一般项目
和一般项目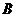 至少有一个被选中的不同选法的种数是
(用数字作
至少有一个被选中的不同选法的种数是
(用数字作
答).
15.设焦点在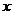 轴上的双曲线
轴上的双曲线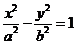 的右准线与两条渐近线交于
的右准线与两条渐近线交于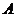 、
、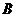 两点,右焦点
两点,右焦点
为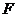 ,且
,且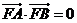 ,则双曲线的离心率
,则双曲线的离心率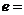 .
.
16.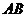 垂直于
垂直于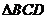 所在的平面,
所在的平面,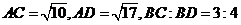 ,当
,当 的
的
面积摄大时,点 到直线
到直线 的距离为
.
的距离为
.
三、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(本小题满分10分)
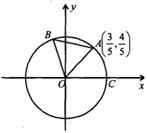 如图
如图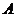 、
、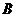 是单位圆
是单位圆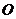 上的点,
上的点,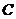 是圆
是圆 与
与 轴正半轴的交点,
轴正半轴的交点, 点的坐标为
点的坐标为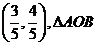 为正三角形.
为正三角形.
(1)求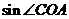 的值;
的值;
(2)求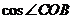 的值;
的值;

18.(本小题满分12分)
因金融危机,某公司的出口额下降,为此有关专家提出两种促进出口的方案,该方案需分两年实施且相互独立,该方案预计第一年可以使出口额恢复到危机前的1.0倍、0.9倍、0.8倍的概率分别为0.2、0.4、0.4;第二年可以使出口额为第一年的1.5倍、1.25倍,1.0倍的概率分别是0.3,0.3,0.4.
(1)求两年后出口额恰好达到危机前出口额的概率;
(2)求两年后出口额超过危机前出口额的概率.


19.(本小题满分12分)
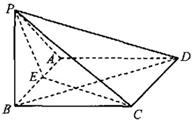 四棱锥
四棱锥 中,底面
中,底面 为矩形,侧面
为矩形,侧面 为正三角形,
为正三角形,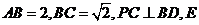 为
为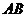 的中点.
的中点.
(1)证明: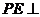 平面
平面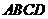 ;
;
(2)求二面角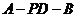 的大小.
的大小.


20.(本小题满分12分)
在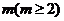 个不同数的非列
个不同数的非列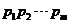 中,若
中,若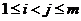 时,
时,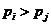 (即前面某数大于后面某数),称
(即前面某数大于后面某数),称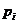 与
与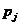 构成一个逆序,一个排列的全部逆序的总数称为该排列的逆序数,记排列
构成一个逆序,一个排列的全部逆序的总数称为该排列的逆序数,记排列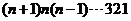 和逆序数为
和逆序数为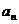 ,如排列21的逆序数
,如排列21的逆序数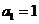 ,排列321的逆序数
,排列321的逆序数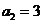 ,排列4321的逆序数
,排列4321的逆序数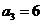 .
.
(1)求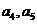 ,并写出
,并写出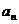 的表达式;
的表达式;
(2)令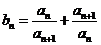 ,
,
证明: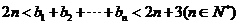



21.(本小题满分12分)
已知函数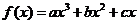 在点
在点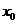 处取得极小值
处取得极小值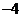 ,使
,使 的
的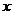 的取值范围是(1,3).
的取值范围是(1,3).
(1)求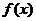 的解析式;
的解析式;
(2)当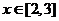 时,求
时,求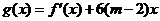 的最大值.
的最大值.



22.(本小题满分12分)
椭圆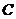 的中心为坐标原点
的中心为坐标原点 ,焦点在
,焦点在 轴上,焦点到相应准线的距离以及离心率均为
轴上,焦点到相应准线的距离以及离心率均为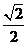 ,直线
,直线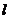 与
与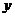 轴交于点
轴交于点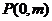 ,与椭圆
,与椭圆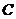 交于相异两点
交于相异两点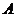 、
、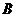 ,且
,且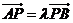 .
.
(1)求椭圆方程;
(2)若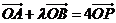 ,求
,求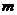 的取值范围.
的取值范围.

1.B 2.B 3.A 4.C 5.C 6.B 7.D 8.B 9.C 10.B 
11.A 12.D
【解析】
1. ,所以选B.
,所以选B.
2. 的系数是
的系数是 ,所以选B.
,所以选B.
3. ,所以选
,所以选 .
.
4. 为钝角或
为钝角或 ,所以选C
,所以选C
5. ,所以选C.
,所以选C.
6. ,所以选B.
,所以选B.
7. ,所以选D.
,所以选D.
8.化为 或
或 ,所以选B.
,所以选B.
9.将 左移
左移 个单位得
个单位得 ,所以选A.
,所以选A.
10.直线 与椭圆
与椭圆 有公共点
有公共点 ,所以选B.
,所以选B.
11.如图,设 ,则
,则 ,
,

 ,
,
 ,从而
,从而 ,因此
,因此 与底面所成角的正弦值等于
与底面所成角的正弦值等于 .所以选A.
.所以选A.
12.画可行域 可知符合条件的点 是:
是: 共6个点,故
共6个点,故 ,所以选D.
,所以选D.
二、
13.185. .
.
14.60. .
.
15. ,由
,由 ,得
,得
 .
.
16. .如图:
.如图:

如图,可设 ,又
,又 ,
,
 .
.
当 面积最大时,
面积最大时, .点
.点 到直线
到直线 的距离为
的距离为 .
.
三、
17.(1)由三角函数的定义知: .
.
(2)


 .
.
18.(1)设两年后出口额恰好达到危机前出口额的事件为 ,则
,则 .
.
(2)设两年后出口额超过危机前出口额的事件为 ,则
,则 .
.
19.(1)设 与
与 交于点
交于点 .
.



从而 ,即
,即 ,又
,又 ,且
,且
 平面
平面 为正三角形,
为正三角形, 为
为 的中点,
的中点,
 ,且
,且 ,因此,
,因此, 平面
平面 .
.
(2) 平面
平面 ,∴平面
,∴平面 平面
平面 又
又 ,∴平面
,∴平面 平面
平面
设 为
为 的中点,连接
的中点,连接 ,则
,则 ,
,
 平面
平面 ,过点
,过点 作
作 ,连接
,连接 ,则
,则 .
.
 为二面角
为二面角 的平面角.
的平面角.
在 中,
中, .
.
又 .
.
20.(1)


(2)

又


综上: .
.
21.(1) 的解集为(1,3)
的解集为(1,3)
∴1和3是 的两根且
的两根且
|