
题目列表(包括答案和解析)
2.(1)当以CD为轴转动时, AB棒切割磁感线,当转到AD边竖直时
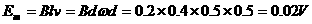 (2分)
(2分)
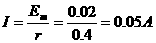 (2分)
(2分)
AB受到的水平外力应等于AB边受到的安培力
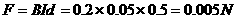 (2分)
(2分)
(2)在转动的过程中,线圈内产生了交变电流,从开始转动到AD边竖直可视为正弦交变电流的0到T/4 (2分)
所以Q=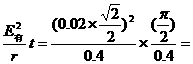 0.00196J(2分)
0.00196J(2分)
(3)当以CD为轴转动时,仅AB棒切割磁感线。
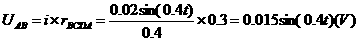 (2分)
(2分)
 当以AB为轴转动时,仅CD棒切割磁感线。
当以AB为轴转动时,仅CD棒切割磁感线。
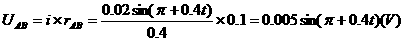 (2分)
(2分)
第一个周期内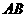 两点间的电势差
两点间的电势差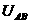 随时间
随时间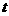 变化的关系为
变化的关系为
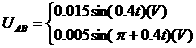
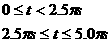
(2分)
1.(1)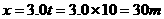 (1分)
(1分)
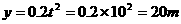 。(1分)
。(1分)
即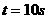 时刻物体的位置坐标为(30,20)(1分)
时刻物体的位置坐标为(30,20)(1分)
(2)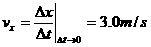 (1分)
(1分) 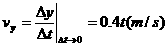 ,(1分)
,(1分)
当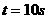 时,
时,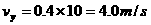 (1分)
(1分)
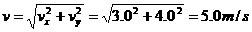 (1分),
(1分),
方向与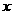 轴正方向夹角为
轴正方向夹角为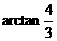 (或满足
(或满足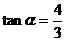 ;或530)(1分)
;或530)(1分)
物体在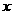 轴方向物体做匀速运动,在
轴方向物体做匀速运动,在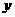 轴方向物体做匀加速运动。
轴方向物体做匀加速运动。
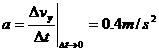 ,沿
,沿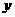 轴正方向(2分)。
轴正方向(2分)。
 (3)如图,摩擦力方向与物体运动方向相反,外力
(3)如图,摩擦力方向与物体运动方向相反,外力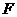 与摩擦力的合力使物体加速。
与摩擦力的合力使物体加速。
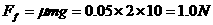 (2分)
(2分)
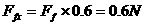 ,
,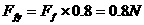 ,
,
根据牛顿运动定律: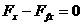 ,解出
,解出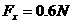
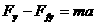 ,解出
,解出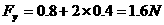 (2分)
(2分)
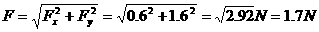 (1分)
(1分)
5.(16分)图中虚线MN是一垂直纸面的平面与纸面的交线,在平面右侧的半空间存在一磁感强度为B的匀强磁场,方向垂直纸面向外。O是MN上的一点,从O点可以向磁场区域发射电量为+q、质量为m、速率为v的粒子,粒子射入磁场时的速度可在纸面内各个方向。已知先后射人的两个粒子恰好在磁场中给定的P点相遇,P到O的距离为L,不计重力及粒子间的相互作用。
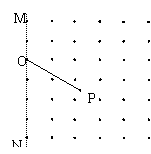 (1)求所考察的粒子在磁场中的轨道半径。
(1)求所考察的粒子在磁场中的轨道半径。
(2)求这两个粒子从O点射人磁场的时间间隔。
4.(16分)如图, 型弯管有一柔软但不可被压缩(或拉伸)的长度为
型弯管有一柔软但不可被压缩(或拉伸)的长度为 的物体,其截面直径比
的物体,其截面直径比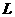 型弯管径略小(管径与物体的长度相比可以忽略),该物体可在
型弯管径略小(管径与物体的长度相比可以忽略),该物体可在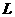 型弯管中移动,且物体在弯角处移动时无能量损失。已知
型弯管中移动,且物体在弯角处移动时无能量损失。已知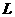 型弯管的竖直部分光滑,水平部分与物体间的动摩擦因数为
型弯管的竖直部分光滑,水平部分与物体间的动摩擦因数为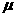 (
(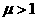 ),且最大静摩擦力等于滑动摩擦力。现让物体在竖直外力作用下保持静止,设物体的上端离水平管的竖直距离为
),且最大静摩擦力等于滑动摩擦力。现让物体在竖直外力作用下保持静止,设物体的上端离水平管的竖直距离为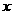 。
。
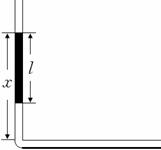 (1)若物体的一部分在水平管中,撤去外力后,物体能在原位置保持静止,求此情况下
(1)若物体的一部分在水平管中,撤去外力后,物体能在原位置保持静止,求此情况下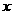 的取值范围。
的取值范围。
(2)若物体全部在竖直管中,撤去外力后,物体能全部进入水平管中,求此情况下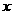 的取值范围。
的取值范围。
(3)若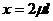 ,求撤去外力后物体右端进入水平管的距离。
,求撤去外力后物体右端进入水平管的距离。
3. (16分)如图所示,光滑水平面上有一小车B,右端固定一个砂箱,砂箱左侧连着一水平轻弹簧,小车和砂箱(包含沙的质量)的总质量为M,车上放有一物块A,质量也是M。物块A和小车以相同的速度v0向右匀速运动。物块A与车面间摩擦不计。车匀速运动时,距砂面H高处有一质量为m(m = M)的泥球自由下落,恰好落在砂箱中。求:在以后的运动过程中,弹簧弹性势能的最大值。
(16分)如图所示,光滑水平面上有一小车B,右端固定一个砂箱,砂箱左侧连着一水平轻弹簧,小车和砂箱(包含沙的质量)的总质量为M,车上放有一物块A,质量也是M。物块A和小车以相同的速度v0向右匀速运动。物块A与车面间摩擦不计。车匀速运动时,距砂面H高处有一质量为m(m = M)的泥球自由下落,恰好落在砂箱中。求:在以后的运动过程中,弹簧弹性势能的最大值。
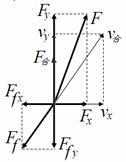
2. (16分)如图所示,空间存在竖直向上的匀强磁场,磁感应强度
(16分)如图所示,空间存在竖直向上的匀强磁场,磁感应强度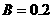 T。一质量
T。一质量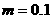 kg,总电阻
kg,总电阻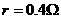 ,边长
,边长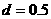 m的正方形均匀导体框平放在粗糙的水平地面上,在一与导体框平面始终垂直的外力作用下做如下运动:首先外力作用在
m的正方形均匀导体框平放在粗糙的水平地面上,在一与导体框平面始终垂直的外力作用下做如下运动:首先外力作用在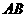 边上,线框绕
边上,线框绕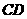 边顺时针转动
边顺时针转动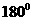 ,然后外力作用到
,然后外力作用到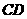 边上,线框绕
边上,线框绕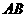 边顺时针转动
边顺时针转动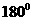 ……如此不断重复,线框在地面上向右翻转,线框转动时的角速度
……如此不断重复,线框在地面上向右翻转,线框转动时的角速度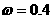 rad/s保持恒定。
rad/s保持恒定。
 (1)线框绕
(1)线框绕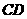 边转动,求当
边转动,求当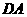 边转到竖直位置时AB边上所加水平外力的大小;
边转到竖直位置时AB边上所加水平外力的大小;
(2)求从线框绕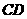 边开始转动到
边开始转动到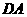 边竖直的这四分之一圈内线框上产生的电热;
边竖直的这四分之一圈内线框上产生的电热;
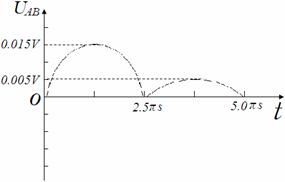
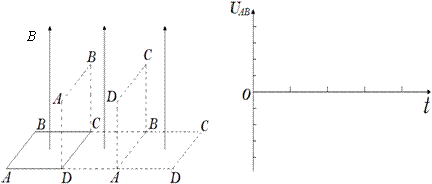
(3)从运动开始作为计时起点,求出在第一个周期内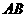 两点间的电势差
两点间的电势差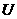 AB随时间
AB随时间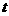 变化的关系,并作出
变化的关系,并作出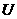 AB随时间
AB随时间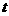 变化的关系图线。
变化的关系图线。
1.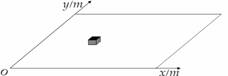 (15分)如图,质量
(15分)如图,质量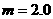 kg的物体在水平外力的作用下在水平面上运动,物体和水平面间的动摩擦因数
kg的物体在水平外力的作用下在水平面上运动,物体和水平面间的动摩擦因数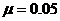 ,已知物体运动过程中的坐标与时间的关系为
,已知物体运动过程中的坐标与时间的关系为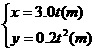 ,
,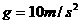 。根据以上条件求:
。根据以上条件求:
(1)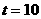 s时刻物体的位置坐标;
s时刻物体的位置坐标;
(2)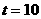 s时刻物体的速度和加速度的大小和方向;
s时刻物体的速度和加速度的大小和方向;
(3)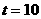 s时刻水平外力的大小。
s时刻水平外力的大小。
4.⑴盒子的初速度为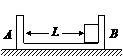
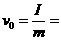 3 m/s (1分)
3 m/s (1分)
设盒子与物块碰撞前的瞬时速度分别为υ1、υ2,根据牛顿第二定律,盒子的加速度为
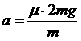 =2μg=2.5 m/s (1分)
=2μg=2.5 m/s (1分)
根据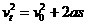 得
得
盒子的碰前速度为
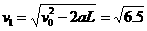 =2.55 m/s (1分)
=2.55 m/s (1分)
因物块与盒子之间无摩擦,所以碰前物块速度为v2=0 (1分)
设碰撞后盒子与物块的瞬时速度分别为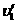 、
、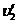 ,由于碰撞时没有机械能损失,由动量守恒和机械能守恒得
,由于碰撞时没有机械能损失,由动量守恒和机械能守恒得
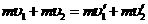 ① (2分)
① (2分)
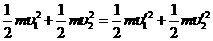 ② (2分)
② (2分)
由①②解得 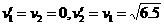 =2.55 m/s (2分)
=2.55 m/s (2分)
即碰撞后交换速度(另一组解为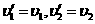 ,表示碰撞前的状态,舍去)
,表示碰撞前的状态,舍去)
⑵设盒子在地面上运动的距离为S,盒子的初速度为υ0,由于碰撞没有能量损失,所有盒子与地面摩擦损失的机械能等于系统损失的总机械能,即有
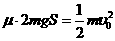 (2分)
(2分)
解得 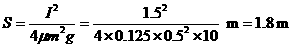 (1分)
(1分)
盒子每前进一个L,物块都要与盒子的左侧内壁碰撞一次,由于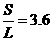 ,所以物块与盒子的左侧内壁共碰撞3次。(2分)
,所以物块与盒子的左侧内壁共碰撞3次。(2分)
⑶整个过程中,对盒子应用动量定理得 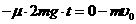 (2分)
(2分)
解得 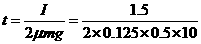 s=1.2 s (1分)
s=1.2 s (1分)
3. (1)由动能定理得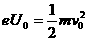
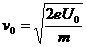
(2)电子不穿出磁场区域的监界半径为d
由动能定理和牛顿第二定律得
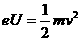
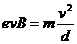
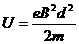 取
取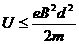
(3)电子的运动轨迹如图
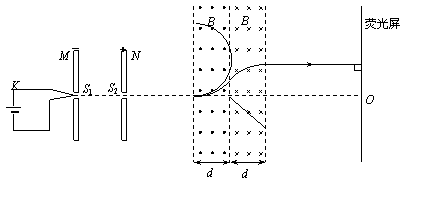
(4)由动能定理、牛顿第二定律及几何关系
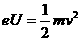
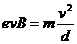
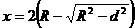
联立得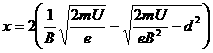
3.(14分)(1) 设稳定时速度为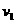 ,当金属棒速度达到稳定时,
,当金属棒速度达到稳定时,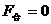
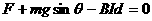 分此时
分此时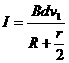
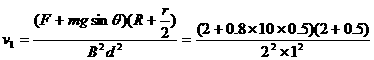
(2)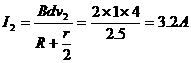
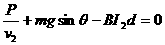
P=9.6w
灯的电压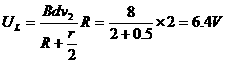
所以电压表的读数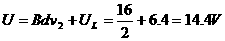
(3)设小灯泡和金属棒产生的热量分别为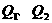 ,
,
由能的转化和守恒可得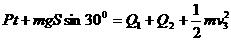
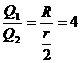 灯泡产生的热量
灯泡产生的热量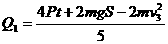
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com