
题目列表(包括答案和解析)
1.(16分)计划发射一颗距离地面高度为地球半径R0的圆形轨道地球卫星,卫星轨道平面与赤道片面重合,已知地球表面重力加速度为g,
(1)求出卫星绕地心运动周期T.
(2)设地球自转周期T0,该卫星绕地旋转方向与地球自转方向相同,则在赤道上一点的人能连续看到该卫星的时间是多少?
3. 

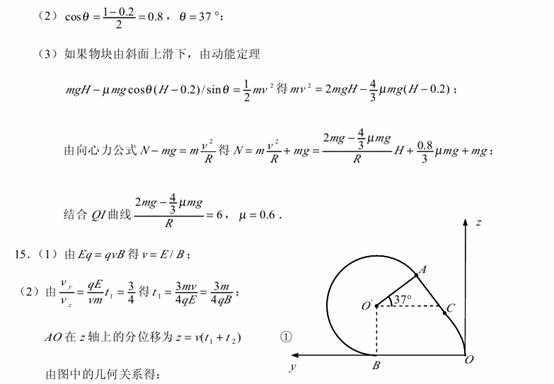
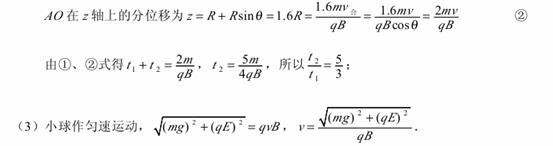
2. 解:(1)第1个铁块放上后,木板做匀减速运动即有:
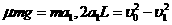 4分
4分
代入数据解得: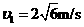 1分
1分
(2)设最终有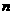 个铁块能放在木板上,则木板运动的加速度大小为
个铁块能放在木板上,则木板运动的加速度大小为
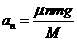 2分
2分
第1个铁块放上后: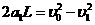
第2个铁块放上后: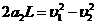
……
第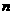 个铁块放上后,
个铁块放上后,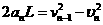
由上可得;(1+2+3+…+n)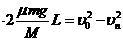 3分
3分
木板停下时,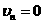 ,得
,得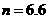 即最终有7个铁块放在木板上 1分
即最终有7个铁块放在木板上 1分
(3)从放上第1个铁块至刚放上第7个铁块的过程中,由(2)中表达式可得:
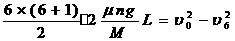 2分
2分
从放上第7个铁块至木板停止运动的过程中,设木板发生的位移 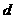 ,则:
,则:
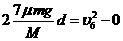 2分
2分
联立解得: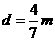 1分
1分
1. 解:(1)小球从A运到O的过程中,根据动能定理:
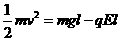 ①2分
①2分
则得小球在 点速度为:
点速度为:
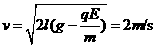 ②2分
②2分
(2)小球运到 点绳子断裂前瞬间,对小球应用牛顿第二定律:
点绳子断裂前瞬间,对小球应用牛顿第二定律:
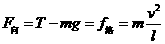 ③2分
③2分
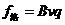 ④1分
④1分
由③、④得:
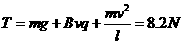 ⑤3分
⑤3分
(3)绳断后,小球水平方向加速度
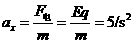 ⑥ 1分
⑥ 1分
小球从 点运动至
点运动至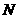 点所用时间
点所用时间
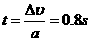 ⑦2分
⑦2分
 间距离
间距离
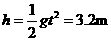 ⑧2分
⑧2分
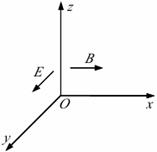
5.(17分)如图所示,某一真空空间内充满着相互垂直的场强为 E 的匀强电场和磁感应强度为 B 的匀强磁场,且电场和磁场根据需要可同时存在或单独存在.在此空间中建立Oxyz 空间直角坐标系,且xOy 位于水平面,
(1)若电场和磁场同时存在,且B 和E 的方向分别与 x 轴和 y 轴正方向相同时,有一电量为 +q 的带电粒子(重力不计)由坐标原点 O 沿 z 轴正方向进入该区域后做匀速直线运动,则该粒子运动速度v为多大?
 (2)若有一电量为+ q的带电粒子(重力不计)由坐标原点O 沿z 轴正方向以(1)问中的速度v 进入该区域后,仅存在电场,且 E 的方向沿 y 轴正方向,当粒子运动方向与 z轴正方向的夹角q
满足tanq=3/4时,撤去电场.经过一段时间后仅加上磁场,且B的方向为 x 轴的负方向,粒子在以后的运动中正好能与y 轴相切.问粒子在无电、磁场时的运动时间为仅受电场力作用时间的多少倍?
(2)若有一电量为+ q的带电粒子(重力不计)由坐标原点O 沿z 轴正方向以(1)问中的速度v 进入该区域后,仅存在电场,且 E 的方向沿 y 轴正方向,当粒子运动方向与 z轴正方向的夹角q
满足tanq=3/4时,撤去电场.经过一段时间后仅加上磁场,且B的方向为 x 轴的负方向,粒子在以后的运动中正好能与y 轴相切.问粒子在无电、磁场时的运动时间为仅受电场力作用时间的多少倍?
(3)若电场和磁场同时存在,且B和E的方向分别与x轴和y轴正方向相同时,有一质量为m、带电量为+ q的带电小球在 yOz平面内做匀速率运动,试判断该小球的运动性质并计算其运动速率.
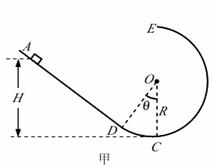
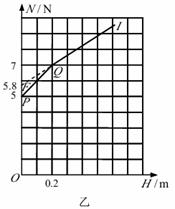
4.(16 分)如图甲所示,一竖内的轨道由粗糙斜面AD 和光滑圆轨道 DCE 组成,AD与DCE 相切于D 点,C为圆轨道的最低点.将物块置于轨道ADC上离地面高为H处由静止下滑,用力传感器测出其经过C 点时对轨道的压力N,改变H 的大小,可测出相应的N 大小,N 随 H 的变化关系如图乙折线PQI 所示(PQ 与 QI 两直线相连接于Q 点),QI 反向延长交纵轴于F 点(0,5.8N),重力加速度g取 10m/s2,求:
(1)小物块的质量m.
(2)圆轨道的半径及轨道DC 所对圆心角q (可用角度的三角函数值表示).
(3)小物块与斜面AD 间的动摩擦因数 m .
3.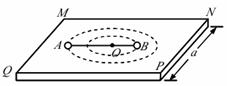 (14分)如图所示,一水平光滑、距地面高为h、边长为a的正方形MNPQ桌面上,用长为 L 的不可伸长的轻绳连接质量分别为mA 、mB
的A、B 两小球.两小球在绳子拉力的作用下,绕绳子上的某点 O 以不同的线速度做匀速圆周运动,圆心O与桌面中心重合.已知m A= 0.5kg,L =1.2m ,L AO = 0.8m,a =2.1m,h = 1.25m ,A球的速度大小v A = 0.4m/s,重力加速度 g取10m/s2,求:
(14分)如图所示,一水平光滑、距地面高为h、边长为a的正方形MNPQ桌面上,用长为 L 的不可伸长的轻绳连接质量分别为mA 、mB
的A、B 两小球.两小球在绳子拉力的作用下,绕绳子上的某点 O 以不同的线速度做匀速圆周运动,圆心O与桌面中心重合.已知m A= 0.5kg,L =1.2m ,L AO = 0.8m,a =2.1m,h = 1.25m ,A球的速度大小v A = 0.4m/s,重力加速度 g取10m/s2,求:
(1)绳子上的拉力F 以及B 球的质量m B;
(2)若当绳子与MN 平行时突然断开,则经过1.5s 两球的距离;
(3)两小球落至地面时,落点的距离.
2.(16分)如图所示,足够长的木板质量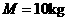 ,放置于光滑水平地面上,以初速度
,放置于光滑水平地面上,以初速度
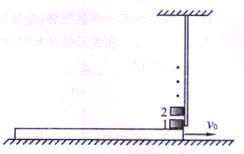
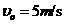 沿水平地面向右匀速运动现有足够多的小铁块,它们的质量均为m=lkg,在木板上方有一固定挡板,当木板运动到其最右端位于挡板正下方时.将一小铁块贴着挡板无初速地放在木板上小铁块与木板的上表面问的动摩擦因数
沿水平地面向右匀速运动现有足够多的小铁块,它们的质量均为m=lkg,在木板上方有一固定挡板,当木板运动到其最右端位于挡板正下方时.将一小铁块贴着挡板无初速地放在木板上小铁块与木板的上表面问的动摩擦因数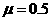 ,当术板运动了
,当术板运动了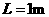 时,又无初速地贴着挡板在第1个小铁块上放上第2个小铁块。只要木板运动了
时,又无初速地贴着挡板在第1个小铁块上放上第2个小铁块。只要木板运动了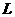 就按同样的方式再放置一个小铁块,直到木板停止运动.(取g=l0m
就按同样的方式再放置一个小铁块,直到木板停止运动.(取g=l0m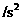 。),试问:
。),试问:
(1)第1个铁块放上后,木板运动了L时,木板的速度多大?
(2)最终木板上放有多步个铁块?
(3)最后一个铁块放上后,木板再向右运动的距离是多少?
1.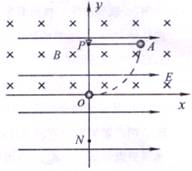 (1 5分)如图所示,竖直平面
(1 5分)如图所示,竖直平面 内存在水平向右的匀强电场,场强大小E=10N/c,在y≥0的区域内还存在垂直于坐标平面向里的匀强磁场,磁感应强度大小B=0.5T一带电量
内存在水平向右的匀强电场,场强大小E=10N/c,在y≥0的区域内还存在垂直于坐标平面向里的匀强磁场,磁感应强度大小B=0.5T一带电量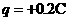 、质量
、质量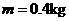 的小球由长
的小球由长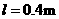 的细线悬挂于
的细线悬挂于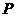 点小球可视为质点,现将小球拉至水平位置A无初速释放,小球运动到悬点
点小球可视为质点,现将小球拉至水平位置A无初速释放,小球运动到悬点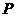 正下方的坐标原点
正下方的坐标原点 时,悬线突然断裂,此后小球又恰好能通过
时,悬线突然断裂,此后小球又恰好能通过 点正下方的N点.(g=10m/s
点正下方的N点.(g=10m/s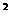 ),求:
),求:
(1)小球运动到 点时的速度大小;
点时的速度大小;
(2)悬线断裂前瞬间拉力的大小;
(3) 间的距离
间的距离
20.(1)对金属块A用动能定理qEL=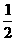 mv02所以电场强度大小E=
mv02所以电场强度大小E=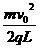 方向水平向右
方向水平向右
(2)A、B碰撞,由系统动量守恒定律得mAv0=mA(-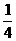 v0)+mBvB
v0)+mBvB
用mB=2m代入解得vB=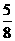 v0 B碰后做匀速运动,碰到挡板的时间tB=
v0 B碰后做匀速运动,碰到挡板的时间tB=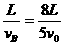
A的加速度aA=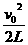 A在tB段时间的位移为sA=vatB+
A在tB段时间的位移为sA=vatB+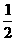 atB2=-
atB2=-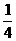 v0·
v0·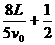 ·
·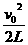 ·(
·(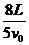 )2=
)2=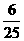 L
L
因sA<L,故A第二次与B相碰必在B与C相碰之后
(3)B与C相碰,由动量守恒定律可得
mBvB=mBvB′+mCvC′ vC′=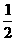 vB vB′=0
vB vB′=0
A从第一次相碰到第二次与B相碰的位移为L,因此电场力做的功
W电=qEL=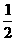 mv02.
mv02.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com