
题目列表(包括答案和解析)
4、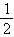 已知二次函数y1=x2-2x-3. (1)结合函数y1的图像,确定当x取什么值时,y1>0,y1=0,y1<0;
已知二次函数y1=x2-2x-3. (1)结合函数y1的图像,确定当x取什么值时,y1>0,y1=0,y1<0;
(2)根据(1)的结论,确定函数y2= (|y1|-y1)关于x的解析式;
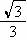 (3)若一次函数y=kx+b(k
(3)若一次函数y=kx+b(k
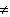 0)的图像与函数y2的图像交于三个不同的点,试确定实数k与b应满足的条件。
0)的图像与函数y2的图像交于三个不同的点,试确定实数k与b应满足的条件。
3、已知:二次函数y=x2-2(m-1)x+m2-2m-3,其中m为实数。
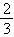 (1)求证:不论m取何实数,这个二次函数的图像与x轴必有两个交点;(2)设这个二次函数的图像与x轴交于点A(x1,0)、B(x2,0),且x1、x2的倒数和为 ,求这个二次函数的解析式。
(1)求证:不论m取何实数,这个二次函数的图像与x轴必有两个交点;(2)设这个二次函数的图像与x轴交于点A(x1,0)、B(x2,0),且x1、x2的倒数和为 ,求这个二次函数的解析式。
2、(1)已知:关于x、y的方程组 有两个实数解,求m的取值范围;
(2)在(1)的条件下,若抛物线y=-(m-1)x2+(m-5)x+6与x轴交于A、B两点,与y轴交于点C,且△ABC的面积等于12,确定此抛物线及直线y=(m+1)x-2的解析式;
(3)你能将(2)中所得的抛物线平移,使其顶点在(2)中所得的直线上吗?请写出一种平移方法。
1、已知:二次函数y=x2-kx+k+4的图象与y轴交于点c,且与x轴的正半轴交于A、B两点(点A在点B左侧)。若A、B两点的横坐标为整数。
(1)确定这个二次函数的解析式并求它的顶点坐标;(2)若点D的坐标是(0,6),点P(t,0)是线段AB上的一个动点,它可与点A重合,但不与点B重合。设四边形PBCD的面积为S,求S与t的函数关系式;
 (3)若点P与点A重合,得到四边形ABCD,以四边形ABCD的一边为边,画一个三角形,使它的面积等于四边形ABCD的面积,并注明三角形高线的长。再利用“等底等高的三角形面积相等”的知识,画一个三角形,使它的面积等于四边形ABCD的面积(画示意图,不写计算和证明过程)。
(3)若点P与点A重合,得到四边形ABCD,以四边形ABCD的一边为边,画一个三角形,使它的面积等于四边形ABCD的面积,并注明三角形高线的长。再利用“等底等高的三角形面积相等”的知识,画一个三角形,使它的面积等于四边形ABCD的面积(画示意图,不写计算和证明过程)。
10.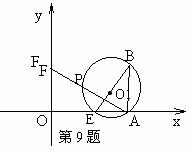 (深圳)如图,等腰梯形ABCD中,AD∥BC,AB=CD,以HF
(深圳)如图,等腰梯形ABCD中,AD∥BC,AB=CD,以HF
为直径的⊙O与AB、BC、CD、DA相切,切点分别是E、F、G、
H.其中H为AD的中点,F为BC的中点。连结HG、GF。
(1)若HG和GF的长是关于x的方程x2-6x+k=0的两个实数根,
求⊙O的直径HF(用含k的代数式表示),并求出k的取值范围。
(2)如图,连结EG、DF。EG与HF交于点M,与DF交于点N,
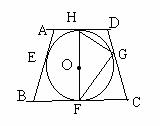
 求
求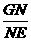 的值。
的值。

9.(武汉)如图,已知:在直角坐标系中,点E从O点出发,以1个
单位/秒的速度沿x轴正方向运动,点F从O点出发,以2个单位/秒
的速度沿y 轴正方向运动。B(4,2)、以BE为直径作⊙O1。
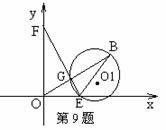 (1)若点E、F同时出发。设线段EF与线段OB交于点G,试判断点
(1)若点E、F同时出发。设线段EF与线段OB交于点G,试判断点
G与⊙O1的位置关系,并证明你的结论;
(2)在(1)的条件下,连结FB、几秒时FB与⊙O1相切?
(3)若点E提前2秒出发,点F再出发。当点F出发后,
E点在A点左侧时,设BA⊥x轴于A点。连结AF交⊙O1于
点P,试问APAF的值是否会发生变化?若不变,请说明理由,
并求其值;若变化,请求其值的变化范围。
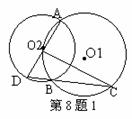
8.(呼和浩特)已知⊙O1与⊙O2相交于A、B两点,
且点O2在⊙O1上。(1)如图1,AD是⊙O2的直径,
连结DB并延长交⊙O1于C,求证:CO2⊥AD.
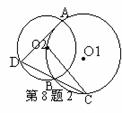 (2)如图2,如果AD是⊙O2的一条弦,连结DB并延长
(2)如图2,如果AD是⊙O2的一条弦,连结DB并延长
交⊙O1于C,那么CO所在直线是否与AD垂直?证明你的结论。
7.(青岛)已知:如图△ABC内接于O ,AB=AC,AO⊥BC于D。
(1)求证:△ABC是等边三角形;
(2)若AB=1,P是劣弧BC上的一个动点(点P与B、C不重合),
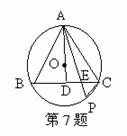 PA交BC于点E,设AE=x,EP=y,求y与x之间的函数关系式,
PA交BC于点E,设AE=x,EP=y,求y与x之间的函数关系式,
并写出自变量x的取值范围;
(3)在(2)的前提下,令∠PAC=α,∠APC=β,
当y取何值时,sin2α+sin2β=1.
6.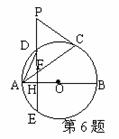 (济南)如图,AB、AC分别是⊙O的直径和弦,D为劣弧AC上一点,
(济南)如图,AB、AC分别是⊙O的直径和弦,D为劣弧AC上一点,
交O于点E,交AC于点F,P为ED的延长线上一点。
(1)当△PCF满足什么条件时,PC与⊙O相切,为什么?
(2)当点D在劣弧AC的什么位置时,才能使AD2=DE·DF,为什么?
5.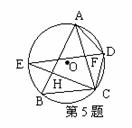 (哈尔滨)如图,△ABC内接于O,BC=4,S△ABC=6
(哈尔滨)如图,△ABC内接于O,BC=4,S△ABC=6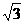 ,∠B为
,∠B为
锐角,且关于x的方程x2-4cosB+1=0有两个相等的实数根.D是
劣弧AC上任一点(点D不与点A、C重合),DE平分∠ADC,
交O于点E,交AC 于点F.(1)求∠B的度数;(2)求CE的长;
(3)求证:DA、DC的长是方程y2-DE·y+DE·DF=0的两个实数根.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com