
题目列表(包括答案和解析)
1.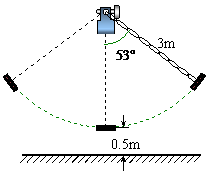 如图所示,秋千链子的长度为3m,静止时的秋千踏板(大小忽略不计)距地面0.5m.秋千向两边摆动时,若最大摆角(摆角指秋千链子与铅垂线的夹角)约为
如图所示,秋千链子的长度为3m,静止时的秋千踏板(大小忽略不计)距地面0.5m.秋千向两边摆动时,若最大摆角(摆角指秋千链子与铅垂线的夹角)约为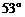 ,则秋千踏板与地面的最大距离约为多少?
,则秋千踏板与地面的最大距离约为多少?
(参考数据: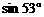 ≈0.8,
≈0.8,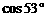 ≈0.6)
≈0.6)
从近几年全国各省市的中考试题来看,直角三角形的解法及其应用,成为中考的热点,它着重考查学生的应用能力与创新能力。
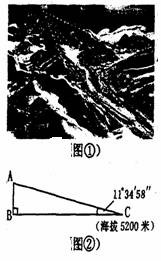 例1.(2005年福建三明市)2005年5月22日,媒体广泛报道了我国“重测珠峰高度”的活动,测量人员从六个不同观察点同时对峰顶进行测量(如图1)。小英同学对此十分关心,从媒体得知一组数据:观察点C的海拔高度为5200米,对珠峰峰顶A点的仰角∠ACB=11°34′58″,AC=18174.16米(如图2),她打算运用已学知识模拟计算。
例1.(2005年福建三明市)2005年5月22日,媒体广泛报道了我国“重测珠峰高度”的活动,测量人员从六个不同观察点同时对峰顶进行测量(如图1)。小英同学对此十分关心,从媒体得知一组数据:观察点C的海拔高度为5200米,对珠峰峰顶A点的仰角∠ACB=11°34′58″,AC=18174.16米(如图2),她打算运用已学知识模拟计算。
⑴现在也请你用此数据算出珠峰的海拔高度(精确到0.01米);
⑵你的计算结果与1975年公布的珠峰海拔高度8848.13米相差多少?珠峰是长高了,不是变矮了呢?
解: ⑴在Rt△ABC中,∵sin∠ACB=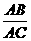
∴AB=AC sin∠ACB=18174.16×sin11°34′58″
≈3649.07
3649.07+5200=8849.07
∴珠峰的海拔高度为8849.07米
⑵8849.07-8848.13=0.94
练习一
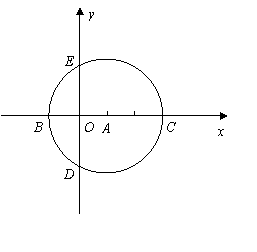
15、如图,在直角坐标系中,以点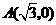 为圆心,以
为圆心,以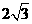 为半径的圆与
为半径的圆与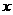 轴相交于点
轴相交于点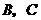 ,与
,与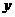 轴相交于点
轴相交于点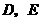 .
.
(1)若抛物线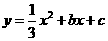 经过
经过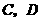 两点,求抛物线的解析式,并判断点
两点,求抛物线的解析式,并判断点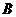 是否在该抛物线上.(6分)
是否在该抛物线上.(6分)
(2)在(1)中的抛物线的对称轴上求一点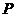 ,使得
,使得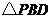 的周长最小.(3分)
的周长最小.(3分)
(3)设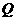 为(1)中的抛物线的对称轴上的一点,在抛物线上是否存在这样的点
为(1)中的抛物线的对称轴上的一点,在抛物线上是否存在这样的点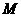 ,使得四边形
,使得四边形 是平行四边形.若存在,求出点
是平行四边形.若存在,求出点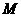 的坐标;若不存在,说明理由.(4分)
的坐标;若不存在,说明理由.(4分)
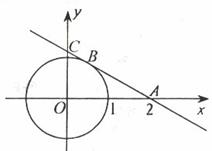
14、如图7 ⊙0的半径为1,过点A(2,0)
⊙0的半径为1,过点A(2,0)
的直线切⊙0于点B,交y轴于点C.
(1)求线段AB的长;
 (2)求以直线AC为图象的一次函数的解析式.
(2)求以直线AC为图象的一次函数的解析式.
13、如图,PA、PB是⊙O的两条切线,
切点分别为A、B 若直径AC=12cm,
若直径AC=12cm,
∠P=600,求弦AB的长.
12、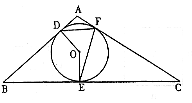 如图,⊙O是△ABC的内切圆,切点分别是D、E、F,已知∠A = 100°,∠C = 30°,则∠DFE的度数是(
)
如图,⊙O是△ABC的内切圆,切点分别是D、E、F,已知∠A = 100°,∠C = 30°,则∠DFE的度数是(
)
A、55° B、60°
C、65° D、70°
11、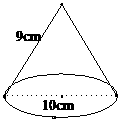 小丽要制作一个圆锥模型,要求圆锥的母线长为
小丽要制作一个圆锥模型,要求圆锥的母线长为
9cm,底面圆的直径为10cm,那么小丽要制作的这个
圆锥的侧面展开扇形的纸片的圆心角度数是( )
A、150° B、200° C、180° D、240°
10、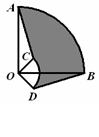 如图4,圆心角都是90°的扇形OAB与扇形OCD叠放在一起,OA=3,OC=1,分别连结AC、BD,则图中阴影部分的面积为( )
如图4,圆心角都是90°的扇形OAB与扇形OCD叠放在一起,OA=3,OC=1,分别连结AC、BD,则图中阴影部分的面积为( )
A. 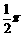 B.
B. 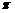 C.
C. 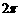 D.
D. 
9、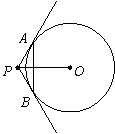 如图,直线
如图,直线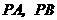 是
是 的两条切线,
的两条切线,
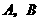 分别为切点,
分别为切点,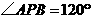 ,
,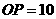 厘米,则弦
厘米,则弦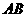 的长为( )
的长为( )
A.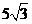 厘米 B.5厘米
厘米 B.5厘米
C.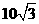 厘米 D.
厘米 D.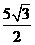 厘米
厘米
8、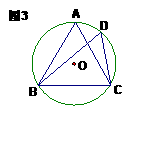 ⊙O是等边三角形ABC的外接圆,点D是⊙O
⊙O是等边三角形ABC的外接圆,点D是⊙O
上一点,则∠BDC = ;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com