
题目列表(包括答案和解析)
6.学校计划将120名学生平均分成若干个读书小组,若每个小组比原计划多1人,则要比原计划少分出6个小组,那么原计划要分成的小组数是
A. 40 B. 30 C. 24 D. 20
5.古代有这样一个寓言故事:驴子和骡子一同走,它们驮着不同袋数的货物,每袋货物都是一样重的。驴子抱怨负担太重,骡子说:“你抱怨干吗?如果你给我一袋,那我所负担的就是你的两倍;如果我给你一袋,我们才恰好驮的一样多!”那么驴子原来所托货物的袋数是
A.5 B.6 C.7 D.8
4.方程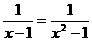 的解是
的解是
A.1 B.-1 C.±1 D.0
3.学校计划将120名学生平均分成若干个读书小组,若每个小组比原计划多1人,则要比原计划少分出6个小组,那么原计划要分成的小组数是
(A) 40 (B) 30 (C) 24 (D) 20
2.若关于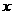 的方程
的方程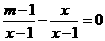 有增根,则
有增根,则 的值是
的值是
A.3 B.2 C.1 D.-1
1.某市为处理污水需要铺设一条长为4000米的管道,为了尽量减少施工对交通所造成的影响,实际施工时每天比原计划多铺设10米,结果提前20天完成任务。设原计划每天铺设管道x米,则可得方程
(A)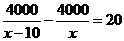 (B)
(B)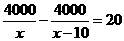
(C)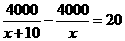 (D)
(D)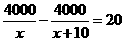
17.(1)设所求抛物线的解析式为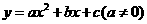 .
.
由题意,得: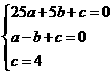 解得:
解得: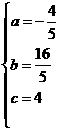
∴所求的解析式为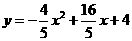 .
.
(2)依题意,分两种情况:
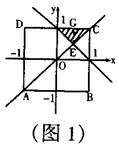
①当点M在原点的左边(如图1)时,
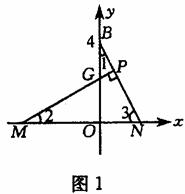 在Rt△BON中,∠1+∠3=90°
在Rt△BON中,∠1+∠3=90°
∵MP⊥BN,∴∠2+∠3=90°
在Rt△BON和Rt△MOG中,
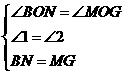
∴Rt△BON≌Rt△MOG. ∴OM=OB=4
∴M点坐标为(-4,0)
②当点M在原点的右边(如图2)时,同理可证:OM=OB=4.
此时M点的坐标为(4,0)
∴M点的坐标为(-4,0)或(-4,0)
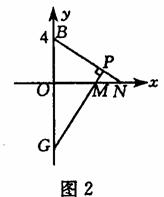 (3)图1中,Rt△BON≌Rt△MOG. ∴OG=ON=t.
(3)图1中,Rt△BON≌Rt△MOG. ∴OG=ON=t.
∴S=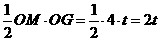 (其中0<t<4)
(其中0<t<4)
图2中,同理可得S=2t,其中t>4.
∴所求的函数关系式为S=2t.
t的取值范围为t>0且t 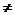 4.
4.
(4)存在点R,使△ORA为等腰三角形.
其坐标为: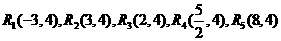 .
.
16.解:(1)当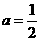 时,如图1,
时,如图1,
直线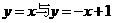 的交点是
的交点是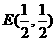
∴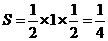
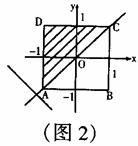 (2)①当
(2)①当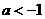 时,如图2,
时,如图2,
△ADC的面积就是S,
∴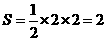
②当-1≤a<0时,如图3,
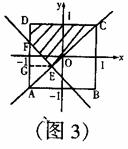 直线
直线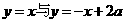 的交点是E(
的交点是E(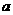 ,
,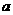 )
)
∴EG=(1- )=1+a AF=2(1+a)
)=1+a AF=2(1+a)
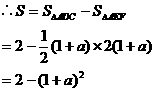
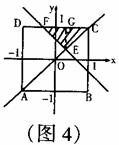 ③当0≤a<1时,如图4,
③当0≤a<1时,如图4,
直线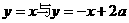 的交点是E(a,a)
的交点是E(a,a)
 ∴EG=1-a CF=2(1-a)
∴EG=1-a CF=2(1-a)
∴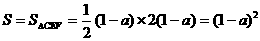
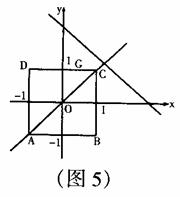
④当a≥1时,如图5,S=0
∴S关于a的函数关系式为
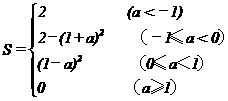
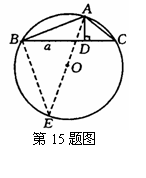
15.解:∵AD与DC的长度为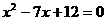 的两根 ∴有两种情况
的两根 ∴有两种情况
①AD=3,DC=4 ②AD=4,DC=3
由勾股定理:求得AC=5,连接AO并延长交⊙O于E点,
连接BE∴∠ABE=90° 又∵∠E=∠C
∴△ABE∽△ADC,
 ∴
∴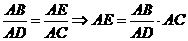
14.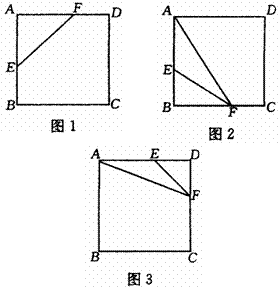 解:分三种情况计算:
解:分三种情况计算:
(1)当AE=AF=10cm时,(如图1),
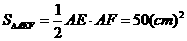
(2)当AE=EF=10cm时(如图2),
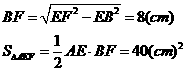
(3)当AE=EF=10cm时(如图3),
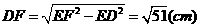
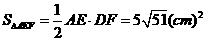 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com