
题目列表(包括答案和解析)
6、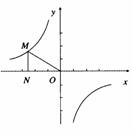 (2007山东枣庄)反比例函数
(2007山东枣庄)反比例函数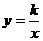 的图象如图所示,点M是该函数图象上一点,MN垂直于x轴,垂足是点N,如果S△MON=2,则k的值为( )D
的图象如图所示,点M是该函数图象上一点,MN垂直于x轴,垂足是点N,如果S△MON=2,则k的值为( )D
(A)2 (B)-2
(C)4 (D)-4
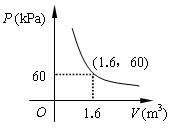
5、(2007山东青岛)某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P ( kPa ) 是气体体积V ( m3 ) 的反比例函数,其图象如图所示.当气球内的气压大于120 kPa时,气球将爆炸.为了安全起见,气球的体积应( ).C
A.不小于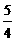 m3 B.小于
m3 B.小于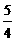 m3 C.不小于
m3 C.不小于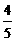 m3 D.小于
m3 D.小于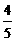 m3
m3
4、(2007山东临沂)已知反比例函数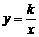 的图象在第二、第四象限内,函数图象上有两点A(
的图象在第二、第四象限内,函数图象上有两点A(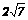 ,y1)、B(5,y2),则y1与y2的大小关系为( )。A
,y1)、B(5,y2),则y1与y2的大小关系为( )。A
 A、y1>y2 B、y1=y2 C、y1<y2 D、无法确定
A、y1>y2 B、y1=y2 C、y1<y2 D、无法确定
3、(2007河北省)如图1,某反比例函数的图像过点M(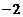 ,1),则此反比例函数
,1),则此反比例函数
表达式为( )B
A.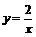 B.
B.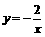
C.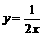 D.
D.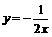
2、(2007湖北孝感)在反比例函数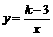 图象的每一支曲线上,y都随x的增大而减小,则k的取值范围是 ( )A
图象的每一支曲线上,y都随x的增大而减小,则k的取值范围是 ( )A
 A.k>3
B.k>0
C.k<3
D. k<0
A.k>3
B.k>0
C.k<3
D. k<0
1、(2007浙江金华)下列函数中,图象经过点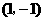 的反比例函数解析式是( )B
的反比例函数解析式是( )B
A.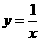 B.
B.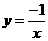 C.
C.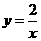 D.
D.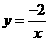
26.已知:如图,在四边形ABCD中,E为AB上一点,△ADE和△BCE都是等边三
角形,AB、BC、CD、DA的中点分别为P、Q、M、N,试判断四边形PQMN为怎样的四边形,并证明你的结论.
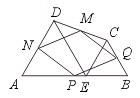
[提示]连结AC和CD,首先利用中位线定理和平行四边形判定定理,证明四边形PQMN为平行四边形,然后证明△AEC≌△DEB,得到AC=BD,再证明□PQMN为菱形.
[答案]四边形PQMN为菱形.证明如下:
 如图,连结AC、BD.
如图,连结AC、BD.
∵ PQ为△ABC的中位线,
∴ PQ
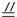
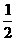 AC.
AC.
同理 MN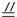
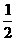 AC.
AC.
∴ MN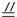 PQ,
PQ,
∴ 四边形PQMN为平行四边形.
在△AEC和△DEB中,
AE=DE,EC=EB,∠AED=60°=∠CEB,
即 ∠AEC=∠DEB.
∴ △AEC≌△DEB.
∴ AC=BD.
∴ PQ=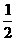 AC=
AC=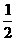 BD=PN.
BD=PN.
∴ □PQMN为菱形.
25.如图,在正方形ABCD中,点E、F分别在BC、CD上移动,但A到EF的距离
AH始终保持与AB长相等,问在E、F移动过程中:
(1)∠EAF的大小是否有变化?请说明理由.
(2)△ECF的周长是否有变化?请说明理由.
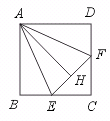
[提示]证明△EAH≌△EAB,△FAH≌△FAD.
[答案](1)∠EAF始终等于45°.证明如下:
在△EAH和△EAB中,
∵ AH⊥EF,∴ ∠AHE=90°=∠B.
又 AH=AB,AE=AE,∴ Rt△EAH≌Rt△EAB.
∴ ∠EAH=∠EAB.
同理 ∠HAF=∠DAF.∴ ∠EAF=∠EAH+∠FAH
=∠EAB+∠FAD=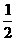 ∠BAD=45°.
∠BAD=45°.
因此,当EF在移动过程中,∠EAF始终为45°角.
(2)△ECF的周长不变.证明如下:
∵ △EAH≌△EAB,
∴ EH=EB.
同理 FH=FD.
∴ △ECF周长=EC+CF+EH+HF
=EC+CF+BE+DF
=BC+CD=定长.
24.如图,在梯形ABCD中,AD∥BC,AB=DC,BD⊥DC于D,且∠C=60°,若
AD=5 cm,求梯形的腰长.
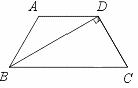
[提示]求出∠CBD,∠ABD和∠ADC的度数,证明AB=AD,或者过D点作DE⊥BC于E,CE为下底与上底的差的一半,又是CD的一半,CD又是BC的一半.从中找出CD与AD的关系.
[解法一]∵ BD⊥CD,∠C=60°,
∴ ∠CBD=30°.
在等腰梯形ABCD中,∠ABC=∠C=60°,
∴ ∠ABD=∠CBD=30°.
∵ AD∥BC,
∴ ∠ADB=∠CBD.
∴ ∠ABD=∠ADB.
∴ AB=AD=5(cm).
[解法二]过D点作DE⊥BC,垂足为E点.
∵ 在Rt△CDE中,∠CDE=30°,
 ∴ CE=
∴ CE=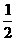 CD.
CD.
又 CE=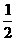 (BC-AD),
(BC-AD),
∴ CD=BC-AD.
即 BC=CD+AD.
又 在Rt△BCD中,∠CBD=30°,
∴ CD=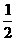 BC.
BC.
∴ CD=2 CD-AD.
即 CD=AD=5(cm).
23.已知:如图,在□ABCD中,BE、CE分别平分∠ABC、∠BCD,E在AD上,
BE=12 cm,CE=5 cm.求□ABCD的周长和面积.
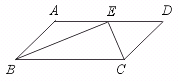
[提示]证明BE⊥EC和E为AD中点.
[答案]在□ABCD中,
∵ AB∥CD,
∴ ∠ABC+∠BCD=180°.
∵ ∠ABE=∠EBC,∠BCE=∠ECD,
∴ ∠EBC+∠BCE=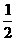 (∠ABC+∠BCD)=90°.
(∠ABC+∠BCD)=90°.
∴ ∠BEC=90°.
∴ BC2=BE2+CE2=122+52=132.
∴ BC=13.
∵ AD∥BC,
∴ ∠AEB=∠EBC.
∴ ∠AEB=∠ABE.
∴ AB=AE.
同理 CD=ED.
∵ AB=CD,
∴ AB=AE=CD=ED=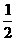 BC=6.5.
BC=6.5.
∴ □ABCD的周长=2(AB+BC)=2(6.5+13)=39.
S□ABCD=2 S△BCE=2·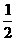 BE·EC
BE·EC
=12×5=60.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com