
题目列表(包括答案和解析)
2. 二次函数中的数形结合[用数形结合思想]
例37(1) 抛物线 y = - 3x2 + 5x - 4开口 ,
y = 4x2 – 6x + 5 开口 .
(2)已知: 二次函数 y = ( m – 3 ) x2 + 2mx + m + 2,其中m 为常数,且满足-2 < m < 3,此抛物线的开口 ,与 x 轴 交点(填有、无),与 y 轴的交点在x 轴 (填上方、下方).
(3) 如果二次函数y = 2x2 + ( 2a – b )x + b,当且仅当
1 < x < 2 时,y < 0,那么 a、b 的值是 .
(4)已知二次函数y=ax2+bx+c,且a<0,a-b+c>0,则一定有 ( )
(A)b2 - 4ac>0 (B)b2 - 4ac=0 (C)b2 - 4ac<0 (D)b2 - 4ac≤0
例38 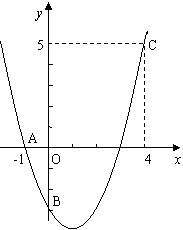 如图,二次函数y=ax2+bx+c的图象经过A、B、C三点.
如图,二次函数y=ax2+bx+c的图象经过A、B、C三点.
1)观察图象写出A、B、C三点的坐标,并求出此二次函数的解析式;
2)求出此抛物线的顶点坐标和对称轴。
|
例39 (1)已知抛物线y=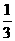 (x - 4)2 - 3的部分图像(如图) 图像再次与x轴相交时的坐标是
( )
(x - 4)2 - 3的部分图像(如图) 图像再次与x轴相交时的坐标是
( )
(A) (5,0) (B) (6,0) (C) (7,0) (D) (8,0)
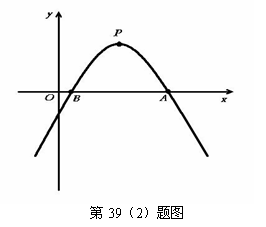
(2)如图,已知二次函数y=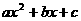 (a≠0)的图象的顶点P的横坐标是4,图象交x轴于点A(m,0)和点B,且m>4,那么AB的长是
( )
(a≠0)的图象的顶点P的横坐标是4,图象交x轴于点A(m,0)和点B,且m>4,那么AB的长是
( )
(A)4+m (B)m (C)2m一8 (D)8-2m
1. 二次函数解析式与它图象上的点[用方程思想]
例33(1)抛物线 y = 2x2 + bx – 5 过点A ( - 2, 9 ),则关于“b”的方程为 ,此抛物线的解析式为 .
(2)(安徽省2003年)已知函数 y = x2 + bx – 1 的图象经过点(3,2).
1)求这个函数的解析式;
2)画出它的图象,并指出图象的顶点坐标;
(3)抛物线 y = 2x2 - 3x – 5 过点A ( n, 9 ),则关于“n”的方程为 ,解得 n = .
(4)抛物线 y = 2x2 + bx – 5 过点A ( - 2, yA ),则 yA =
(5) 二次函数 y = ax2 + bx+ c的图象的顶点A 的坐标为 ( 1, - 3 ),且经过点 B ( -1, 5 ),则设 y = , 得方程为 ,解得 ,此函数解析式为 . (优选顶点式)
(6)二次函数 y = ax2 + bx + c的图象与 x 轴交于点A ( - 3, 0 ),对称轴x = -1,顶点C到x轴的距离为2,则设 y = , 得方程为 ,解得 ,此函数解析式为 . (优选顶点式)
例34(1) y = - 2x2 + 5x – 3 与 y轴的交点的坐标为 ,
(2) y = 2x2 – 5x + c 与 y 轴的交点为( 0,3 ),则有c = .
(3) y = - 2x2 + 5x – 3 与x 轴的交点坐标为 、 .
(4)(安徽省2003年)已知函数 y = x2 + bx – 1 的图象经过点(3,2).
1)求这个函数的解析式;
2)画出它的图象,并指出图象的顶点坐标;
例35 (1)(常州市2002年)抛物线y = x2 - 6x + c 的顶点在 x轴上,则 c 的值是( ).
(A) 9 (B) 3 (C) - 9 (D) 0
( 顶点在 x轴上、抛物线与轴相切、抛物线与轴有且仅有一个交点
← → △ = b2 – 4ac = 0)
(2)抛物线 y = - x2 + 4x + n - 2 的顶点 P 在 x 轴上,求此抛物线与两坐标轴的交点的坐标.
例36(1) 抛物线y = - 2 ( x – 3 )2 – 7 对称轴 x = ,
顶点坐标为 ;
(2) 抛物线 y = 2x2 + 12x – 25 化为 ,
对称轴 x = , 顶点坐标为 .
(3)(河北省2004)若将二次函数y=x2-2x + 3配方为y =(x-h)2 + k的形式,则y=
(4)(贵州市课改实验区2004)抛物线y= - 4(x+2)2+5的对称轴是 。
4. 相关的综合题
 例32 (1)已知一次函数 y = kx
+ b的图象经过第一、二、四象限,则反比例函数 y =
例32 (1)已知一次函数 y = kx
+ b的图象经过第一、二、四象限,则反比例函数 y = 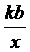 的图象是(
).
的图象是(
).
(A) 第一、二象限 (B) 第三、四象限
(C) 第一、三象限 (D) 第二、四象限
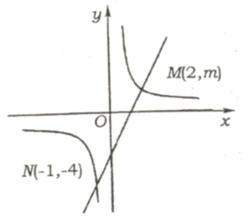
(2)(贵阳市课改实验区2004)如图,一次函数y =
ax + b的图像与反比例函数y = 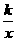 的图象交于M、N两点
的图象交于M、N两点
1)求反比例函数和一次函数的解析式;
2)根据图象写出使反比例函数的值大于一次函数的值的x的取值范围。
(3)已知一次函数y = kx + k的图象与反比例函数y = 的图象交于点P(4,n)。
1)求n的值。 2)求一次函数的解析式。
二次函数
3. 反比例函数的应用
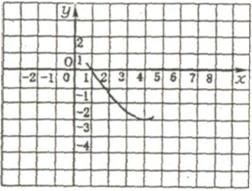
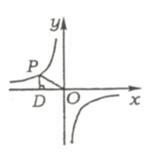 例31如图,点P是反比例函数y =
例31如图,点P是反比例函数y = 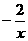 上的一点,PD⊥x轴于点D,则△POD的面积为_______.
上的一点,PD⊥x轴于点D,则△POD的面积为_______.
5. 相关综合题
例47已知抛物线y=x2+bx+c与x轴只有一个交点,且交点为A(2,0).
(I)求b、c的值;
(II)若抛物线与y轴的交点为B,坐标原点为O,求△OAB的周长(答案可带根号)
例48已知一次函数 y = ax + c 与二次函数 y = ax2 + bx + c,它们在同一坐标系内的大致图象是( ).
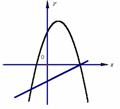
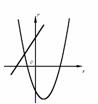
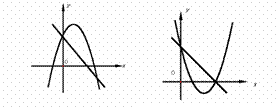 (A) (B) (C)
(D)
(A) (B) (C)
(D)
例49 抛物线 y = x2 - 2x + c 与 x 轴交于A、B两点(点A在点B的左侧),与 y 轴交于点C,且OC =OB,求此抛物线的函数解析式及三角形ABC的面积.
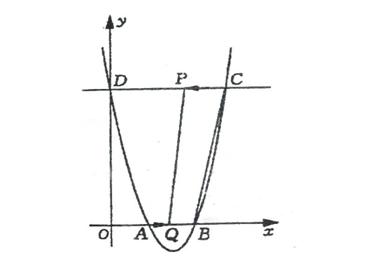 例50如图、已知抛物线y=x2 –ax+a+2与x轴交于A、B两点,与y轴交于点D(0,8),直线DC平行于x轴,交抛物线于另一点C。动点P以每秒2个单位长度的速度从点C出发,沿C→D运动,同时,点Q以每秒1个单位长度的速度从A出发,沿A→B运动。连结PQ、CB.设点P的运动时间为t秒
.
例50如图、已知抛物线y=x2 –ax+a+2与x轴交于A、B两点,与y轴交于点D(0,8),直线DC平行于x轴,交抛物线于另一点C。动点P以每秒2个单位长度的速度从点C出发,沿C→D运动,同时,点Q以每秒1个单位长度的速度从A出发,沿A→B运动。连结PQ、CB.设点P的运动时间为t秒
.
(1)求a的值;
(2)当t为何值时,PQ平行于y轴?
(3)当四边形PQBC的面积等于14时,
求t的值
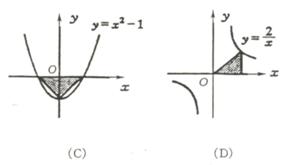
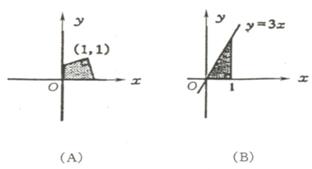
例51 下列图中阴影部分的面积与算式|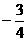 |+(
|+(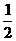 )2
+ 2-1的结果相同的是 ( )
)2
+ 2-1的结果相同的是 ( )
例52 已知抛物线y = x2 + (2n–1)x + n2–1(n为常数)
(1)当该抛物线经过坐标原点,并且顶点在第四象限时,求出它所对应的函数关系式;
(2)设A是(1)所确定的抛物线上位于x轴的下方,且在对称轴左侧的一个动点,过A作x轴的平行线,交抛物线与另一点D,再作AB⊥x轴于B,DC⊥x轴于C.
①当BC=1时,求矩形ABCD的周长;
②试问矩形ABCD的周长是否存在最大值?如果存在,请求出这个最大值,并指出此时A点的坐标;如果不存在,请说明理由。
4. 二次函数的应用
 例45 如图,大拇指与小拇指尽量张开时,两指尖的距离称为指距. 某项研究表明,一般情况下人的身高h是指距d的一次函数. 下表是测得的指距与身高的一组数据:
例45 如图,大拇指与小拇指尽量张开时,两指尖的距离称为指距. 某项研究表明,一般情况下人的身高h是指距d的一次函数. 下表是测得的指距与身高的一组数据:
|
指距d(cm) |
20 |
21 |
22 |
23 |
|
身高h(cm) |
160 |
169 |
178 |
187 |
(1) 求出h与d之间的函数关系式(不要求写出自变量d的取值范围):
(2) 某人身高为196cm,一般情况下他的指距应是多少?
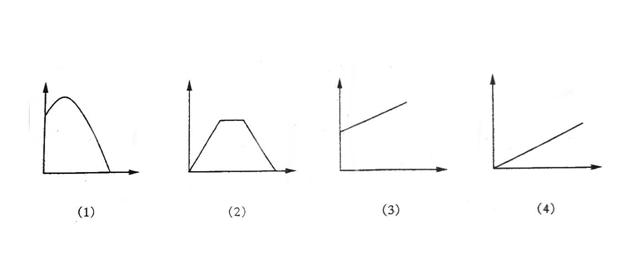 例46若用(1)、(2)、(3)、(4)四幅图像分别表示量之间的关系,请按图像所给顺序,将下面的a、b、c、d对应排序
例46若用(1)、(2)、(3)、(4)四幅图像分别表示量之间的关系,请按图像所给顺序,将下面的a、b、c、d对应排序
(a) 小车从光滑的斜面上滑下(小车速度与时间的关系)
(b) 一个弹簧不挂重物到逐渐挂重物(弹簧长度与所挂重物重量的关系)
(c) 运动员推出去的铅球(铅球高度与时间的关系)
(d) 小杨从A到B后,停留一段时间,然后按原速度返回(路程与时间的关系)
正确的顺序是:( )
(A)(c)(d)(b)(a) (B)(a)(b)(c)(d)
(C)(b)(c)(a)(d) (D)(d)(a)(c)(b)
21.(8分)已知二次函数y=ax2+bx+c 的图象抛物线G 经过(-5,0),(0,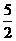 ),(1,6)三点,直线l 的解析式为y=2 x-3.(1)求抛物线G 的函数解析式;(2)求证抛物线G 与直线l 无公共点;(3)若与l 平行的直线y=2 x+m 与抛物线G 只有一个公共点P,求P 点的坐标.
),(1,6)三点,直线l 的解析式为y=2 x-3.(1)求抛物线G 的函数解析式;(2)求证抛物线G 与直线l 无公共点;(3)若与l 平行的直线y=2 x+m 与抛物线G 只有一个公共点P,求P 点的坐标.
[分析](1)略;(2)要证抛物线G 与直线l 无公共点,就是要证G 与l 的解析式组成的方程无实数解;(3)直线y=2 x+m 与抛物线G 只有一个公共点,就是由它们的解析式组成的二元二次方程组有一个解,求出这组解,就得P 点的坐标.
[解](1)∵ 抛物线G 通过(-5,0),(0,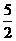 ),(1,6)三点,
),(1,6)三点,
∴
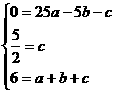 ,
,
解得
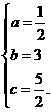
∴ 抛物线G的解析式为y=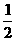 x2+3 x+
x2+3 x+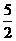 .
.
(2)由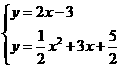 ,
,
消去y,得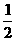 x2+x+
x2+x+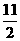 =0,
=0,
∵ D=12-4×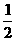 ×
×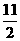 =-10<0,
=-10<0,
∴ 方程无实根,即抛物线G 与直线l 无公共点.
(3)由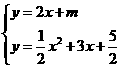 ,消去y,得
,消去y,得
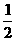 x2+x+
x2+x+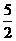 -m=0.
①
-m=0.
①
∵ 抛物线G 与直线y=2 x+m 只有一个公共点P,
∴ D =12-4×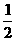 ×(
×(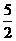 -m)=0.
-m)=0.
解得m=2.
把m=2代入方程①,解得x=-1.
把x=-1代入y=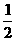 x2+3 x+
x2+3 x+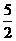 ,得y=0.
,得y=0.
∴ P(-1,0).
[点评]本题综合运用了二次函数解析式的求法.抛物线与直线的交点等知识,其关键是把函数问题灵活转化为方程知识求解.
20.(8分)如图是某市一处十字路口立交桥的横断面在平面直角坐标系中的一个示意图,横断面的地平线为x 轴,横断面的对称轴为y 轴,桥拱的D′GD 部分为一段抛物线,顶点G 的高度为8米,AD 和AD′是两侧高为5.5米的立柱,OA 和OA′为两个方向的汽车通行区,宽都为15米,线段CD 和CD′为两段对称的上桥斜坡,其坡度为1∶4.(1)求桥拱DGD′所在抛物线的解析式及CC′的长.(2)BE 和B′E′为支撑斜坡的立柱,其高都为4米,相应的AB 和A′B′为两个方向的行人及非机动车通行区,试求AB 和A′B′的宽.(3)按规定,汽车通过桥下时,载货最高处和桥拱之间的距离不可小于0.4米,今有一大型运货汽车,装载上大型设备后,其宽为4米,车载大型设备的顶部与地面的距离为7米,它能否从OA(OA′)安全通过?请说明理由.
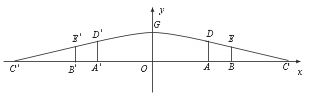
[分析]欲求函数的解析式,关键是求出三个独立的点的坐标,然后由待定系数法求之.所以关键是由题中线段的长度计算出D、G、D′的坐标,当然也可由对称轴x=0解之.
至于求CC′、AB、A′B′的数值,则关键是由坡度的定义求解之;到底能否安全通过,则只需在抛物线的解析式中令x=4,求出相应的y 值,即可作出明确的判断.
[解](1)由题意和抛物线的对称轴是x=0,可设抛物线的解析式为y=ax2+c.
由题意得G(0,8),D(15,5.5)
∴ 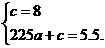
∴ 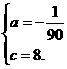
∴ y=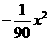 +8.
+8.
又 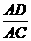 =
=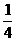 且AD=5.5,
且AD=5.5,
∴ AC=5.5×4=22(米).
∴ CC′=2C=2×(OA+AC)=2×(15+22)=74(米).
∴ CC′的长是74米.
(2)∵ 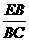 =
=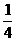 ,BE=4,
,BE=4,
∴ BC=16.
∴ AB=AC-BC=22-16=6(米).
A′B′=AB=6(米).
(3)此大型货车可以从OA(OA′)区域安全通过.
在y=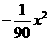 +8中,当x=4时,y=-
+8中,当x=4时,y=-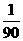 ×16+8=
×16+8=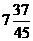 ,而
,而
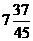 -(7+0.4)=
-(7+0.4)=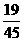 >0,
>0,
∴ 可以从OA 区域安全通过.
19.(8分)已知正比例函数y=4 x,反比例函数y=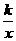 .(1)当k 为何值时,这两个函数的图象有两个交点?k 为何值时,这两个函数的图象没有交点?(2)这两个函数的图象能否只有一个交点?若有,求出这个交点坐标;若没有,请说明理由.
.(1)当k 为何值时,这两个函数的图象有两个交点?k 为何值时,这两个函数的图象没有交点?(2)这两个函数的图象能否只有一个交点?若有,求出这个交点坐标;若没有,请说明理由.
[解]由y=4 x 和y=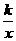 ,得
,得
4 x2-k=0,D =16 k.
(1)当D >0,即k>0时,两函数图象有两个交点;
当D <0,即k<0时,两函数图象没有交点;
(2)∵ 比例系数k≠0,故D ≠0.
∴ 两函数图象不可能只有一个交点.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com