
题目列表(包括答案和解析)
8.某乡的粮食总产量为a(a 为常数)吨,设这个乡平均每人占有粮食为y(吨),人口数为x,则y 与x 之间的函数关系为……………………………………………( )
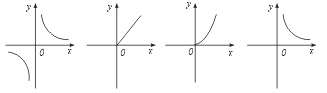
(A) (B) (C) (D)
[提示]粮食总产量一定,则人均占有粮食与人口数成反比,即y=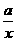 .又因为人口数不为负数,故图象只能是第一象限内的一个分支.
.又因为人口数不为负数,故图象只能是第一象限内的一个分支.
[答案]D.
[点评]本题考查反比例函数图象在实际问题中的应用.(A)错在画出了x<0时的图象,而本题中x 不可能小于0.
7.已知函数y=x2-1840 x+1997与x 轴的交点是(m,0)(n,0),则(m2-1841 m+1997)(n2-1841 n+1997)的值是……………………………………………( )
(A)1997 (B)1840 (C)1984 (D)1897
[提示]抛物线与x 轴交于(m,0)(n,0),则m,n 是一元二次方程x2-1840 x+1997=0的两个根.所以m2-1840 m+1997=0,n2-1840 n+1997=0,mn=1997.
原式=[(m2-1840 m+1997)-m][(n2-1840 n+1997)-n]=mn=1997.
[答案]A.
[点评]本题揭示了二次函数与一元二次方程间的联系,应用了方程的根的定义、根与系数的关系等知识点,并要灵活地把所求代数式进行适当的变形.
6.直线y=ax+c 与抛物线y=ax2+bx+c 在同一坐标系内大致的图象是……( )
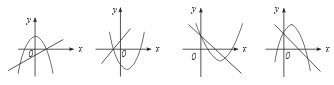
(A) (B) (C) (D)
[提示]两个解析式的常数项都为c,表明图象交于y 轴上的同一点,排除(A),(B).再从a 的大小去判断.
[答案]D.
[点评]本题综合运用了一次函数、二次函数的性质.(B)错误的原因是由抛物线开口向上,知a>0,此时直线必过第一、三象限.
5.若点A(1,y1),B(2,y2),C(p,y3)在反比例函数y=-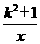 的图象上,则(
)
的图象上,则(
)
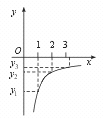
(A)y1=y2=y3 (B)y1<y2<y3 (C)y1>y2>y3 (D)y1>y3>y2
[提示]因-(k2+1)<0,且-(k2+1)=y1=2 y2=p y3,故y1<y2<y3.或用图象法求解,因-(k2+1)<0,且x 都大于0,取第四象限的一个分支,找到在y 轴负半轴上y1,y2,y3 的相应位置即可判定.
[答案]B.
[点评]本题是反比例函数图象的性质的应用,图象法是最常用的方法.在分析时应注意本题中的-(k2+1)<0.
4.如图,已知A,B 是反比例函数y=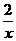 的图象上两点,设矩形APOQ 与矩形MONB 的面积为S1,S2,则………………………………………………………………( )
的图象上两点,设矩形APOQ 与矩形MONB 的面积为S1,S2,则………………………………………………………………( )
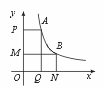
(A)S1=S2 (B)S1>S2 (C)S1<S2 (D)上述(A)、(B)、(C)都可能
[提示]因为SAPOQ=|k|=2,SMONB=2,故S1=S2.
[答案]A.
[点评]本题可以推广为:从双曲线上任意一点向两坐标轴引垂线,由这点及两个垂足和原点构成的矩形的面积都等于|k|.
3.若一元二次方程x2-2 x-m=0无实数根,则一次函数y=(m+1)x+m-1的图象不经过…………………………………………………………………………………( )
(A)第一象限 (B)第二象限 (C)第三象限 (D)第四象限
[提示]由D =4+4 m<0,得m+1<0,则m-1<0,直线过第二、三、四象限.
[答案]A.
[点评]本题综合运用了一元二次方程根的判别式及一次函数图象的性质.注意,题中问的是一次函数图象不经过的象限.
2.二次函数y=ax2+bx+c 的图象如图,则下列各式中成立的个数是…………( )
(1)abc<0; (2)a+b+c<0; (3)a+c>b; (4)a<-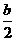 .
.
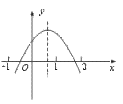
(A)1 (B)2 (C)3 (D)4
[提示]由图象知a<0,-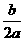 >0,故b>0,而c>0,则abc<0.当x=1时,y>0,即a+c-b>0;当x=-1时,y<0,即a+c-b<0.
>0,故b>0,而c>0,则abc<0.当x=1时,y>0,即a+c-b>0;当x=-1时,y<0,即a+c-b<0.
[答案]B.
[点评]本题要综合运用抛物线性质与解析式系数间的关系.因a<0,把(4)a<-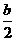 两边同除以a,得1>-
两边同除以a,得1>-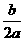 ,即-
,即-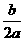 <1,所以(4)是正确的;也可以根据对称轴在x=1的左侧,判断出-
<1,所以(4)是正确的;也可以根据对称轴在x=1的左侧,判断出-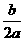 <1,两边同时乘a,得a<-
<1,两边同时乘a,得a<-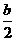 ,知(4)是正确的.
,知(4)是正确的.
1.直线y=3 x-1与y=x-k 的交点在第四象限,则k 的范围是………………( )
(A)k<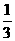 (B)
(B)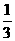 <k<1 (C)k>1 (D)k>1或k<1
<k<1 (C)k>1 (D)k>1或k<1
[提示]由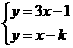 ,解得
,解得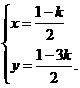 因点在第四象限,故
因点在第四象限,故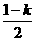 >0,
>0,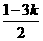 <0.
<0.
∴ 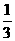 <k<1.
<k<1.
[答案]B.
[点评]本题应用了两函数图象交点坐标的求法,结合了不等式组的解法、象限内点的坐标符号特征等.
9、(2006临安)如图,△OAB是边长为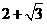 的等边三角形,其中O是坐标原点,顶点B在
的等边三角形,其中O是坐标原点,顶点B在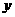 轴正方向上,将△OAB 折叠,使点A落在边OB上,记为A′,折痕为EF.
轴正方向上,将△OAB 折叠,使点A落在边OB上,记为A′,折痕为EF.
(1)当A′E//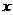 轴时,求点A′和E的坐标;
轴时,求点A′和E的坐标;
(2)当A′E//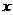 轴,且抛物线
轴,且抛物线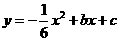 经过点A′和E时,求抛物线与
经过点A′和E时,求抛物线与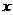 轴的交点的坐标;
轴的交点的坐标;
(3) 当点A′在OB上运动,但不与点O、B重合时,能否使△A′EF成为直角三角形?若能,请求出此时点A′的坐标;若不能,请你说明理由.
[解析](1)由已知可得∠A,OE=60o , A,E=AE
由A′E//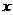 轴,得△OA,E是直角三角形,
轴,得△OA,E是直角三角形,
设A,的坐标为(0,b)
AE=A,E=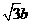 ,OE=2b
,OE=2b
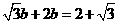
所以b=1,A,、E的坐标分别是(0,1)与(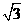 ,1)
,1)
(2) 因为A,、E在抛物线上,所以
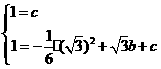
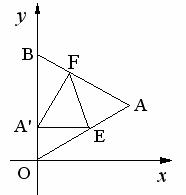 所以
所以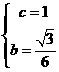 ,函数关系式为
,函数关系式为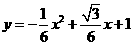
由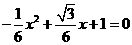 得
得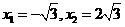
与x轴的两个交点坐标分别是(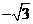 ,0)与(
,0)与(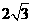 ,0)
,0)
(3) 不可能使△A′EF成为直角三角形。
∵∠FA,E=∠FAE=60o,若△A′EF成为直角三角形,只能是∠A,EF=90o或∠A,FE=90o
若∠A,EF=90o,利用对称性,则∠AEF=90o, A,、E、A三点共线,O与A重合,与已知矛盾;
同理若∠A,FE=90o也不可能
所以不能使△A′EF成为直角三角形。
8、(2006吉林长春)如图,在平面直角坐标系中,两个函数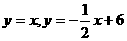 的图象交于点A。动点P从点O开始沿OA方向以每秒1个单位的速度运动,作PQ∥x轴交直线BC于点Q,以PQ为一边向下作正方形PQMN,设它与△OAB重叠部分的面积为S。
的图象交于点A。动点P从点O开始沿OA方向以每秒1个单位的速度运动,作PQ∥x轴交直线BC于点Q,以PQ为一边向下作正方形PQMN,设它与△OAB重叠部分的面积为S。
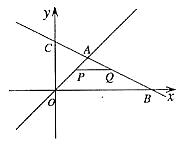 (1)求点A的坐标。
(1)求点A的坐标。
(2)试求出点P在线段OA上运动时,S与运动时间t(秒)的关系式。
(3)在(2)的条件下,S是否有最大值?若有,求出t为何值时,S有最大值,并求出最大值;若没有,请说明理由。
(4)若点P经过点A后继续按原方向、原速度运动,当正方形PQMN与△OAB重叠部分面积最大时,运动时间t满足的条件是____________。
[解析]
(1)由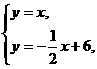 可得
可得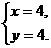
∴A(4,4)。
(2)点P在y = x上,OP = t,
则点P坐标为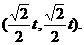
点Q的纵坐标为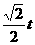 ,并且点Q在
,并且点Q在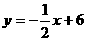 上。
上。
∴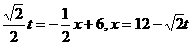 ,
,
即点Q坐标为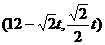 。
。
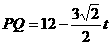 。
。
当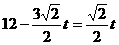 时,
时,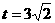 。
。
当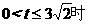 ,
,
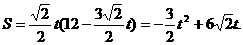
当点P到达A点时,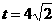 ,
,
当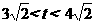 时,
时,
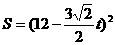
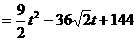 。
。
(3)有最大值,最大值应在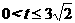 中,
中,
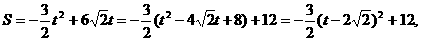
当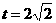 时,S的最大值为12。
时,S的最大值为12。
(4)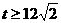 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com