
题目列表(包括答案和解析)
5、、正比例函数y=kx的图象:
过(0,0),(1,K)两点的一条直线.
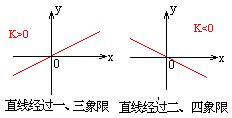
4、正比例函数: 如果y=kx(k是常数,k≠0),那么,y叫做x的正比例函数.
3、自变量的取值范围:对于实际问题,自变量取值必须使实际问题有意义。对于纯数学问题,自变量取值应保证数学式子有意义。
2、函数的概念:设在某个变化过程中有两个变量x、y,如果对于x在某一范围内的每一个确定的值,y都有唯一确定的值与它相对应,那么就说y是x的函数,x叫做自变量。
1、平面直角坐标系:平面内两条有公共原点且互相垂直的数轴构成了平面直角坐标系,坐标平面内一点对应的有序实数对叫做这点的坐标。在平面内建立了直角坐标系,就可以把“形”(平面内的点)和“数”(有序实数对)紧密结合起来。
20.(10分)已知x 轴上有两点A(x1,0),B(x2,0),在y 轴上有一点C,x1,x2 是方程x2-m2x-5=0的两个根,且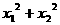 =26,△ABC 的面积是9.(1)求A,B,C 三点的坐标;(2)求过A,B,C 三点的抛物线的解析式.
=26,△ABC 的面积是9.(1)求A,B,C 三点的坐标;(2)求过A,B,C 三点的抛物线的解析式.
[解](1)∵ x1+x2=m2,x1x2=-5,
∴ 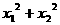 =(x1+x2 )2-2 x1x2=m4+10=26.
=(x1+x2 )2-2 x1x2=m4+10=26.
∴ m2=4,则方程为x2-4 x-5=0.
故x1=5,x2=-1.
∴ A(-1,0),B(5,0)或A(5,0),B(-1,0).
设C点坐标为(0,c).
∵ AB=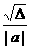 =6,S△ABC=
=6,S△ABC=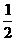 AB·|h|=9,
AB·|h|=9,
∴ h=±3.
∴ C(0,3)或(0,-3).
(2)抛物线的解析式为
y=-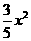 +
+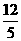 x+3或y=
x+3或y=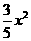 -
-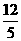 x-3.
x-3.
19.(8分)某商场销售一批衬衫,平均每天可售出20件,每件盈利40元,为扩大销售增加盈利,尽快减少库存,商场决定采取降价措施,经调查发现,若每件衬衫每降价1元,商场平均每天可以多售出2件.(1)若每件降价x 元,每天盈利y 元,求y 与x 的关系式.(2)若商场平均每天要盈利1200元,每件衬衫应降价多少元?(3)每件衬衫降价多少元时,商场每天盈利最多?盈利多少元?
[解](1)y=(40-x )(2 x+20)=-2 x2+60 x+800.
(2)当y=1200时,
-2 x2+60 x+800=1200,
∴ x1=10,x2=20.
∵ 要尽快减小库存,
∴ x=20.
(3)y=-2(x-15)2+1250,故每件降价15元时,最多盈利可达1250元.
[点评]要注意尽量减少库存的隐含条件.
18.(8分)已知二次函数y=2 x2-4 x-6.
(1)求图象的开口方向、对称轴、顶点坐标,并画出草图.
(2)求图象与x 轴的交点坐标,与y 轴的交点坐标.
(3)当x 为何值时,y 随x 的增大而增大?
(4)x 为何值时y≥0?
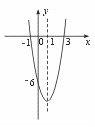
[解](1)图象开口向上,对称轴为x=1,顶点坐标为(1,-8);
(2)与x 轴交于(-1,0),(3,0)两点,与y 轴交于(0,-6);
(3)当x>1时,y 随x 增大而增大;
(4)当x≤-1或x≥3时,y≥0.
17.(8分)按下列条件,求二次函数的解析式:
(1)图象经过A(0,1),B(1,3),C(-1,1);
(2)图象经过(3,1),且当x=2时有最大值为3.
[答案](1)y=x2+x+1;(2)y=-2 x2+8 x-5.
[点评]要会用待定系数法求抛物线的解析式,(2)中隐含顶点坐标为(2,3).
16.(6分)已知正比例函数的图象经过点(1,-2),求此函数的解析式,并在坐标系中画出此函数的图象.
 [解]设正比例函数解析式为y=kx(k≠0).
[解]设正比例函数解析式为y=kx(k≠0).
∵ 图象过(1,-2),
∴ -2=k.
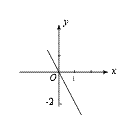
∴ 函数解析式为y=-2 x.
其图象如右图所示.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com