
题目列表(包括答案和解析)
3.如果反比例函数y=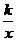 的图象经过点(-2,-1),那么当x>0时,图象所在象限是( )
的图象经过点(-2,-1),那么当x>0时,图象所在象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.反比例函数y=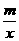 的图象两支分布在第二、四象限,则点(m,m-2)在(
)
的图象两支分布在第二、四象限,则点(m,m-2)在(
)
A.第一象限 B.第二象限 C.第三象限 D.第四象限
1.在下列函数表达式中,x均表示自变量:①y=-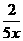 ,②y=
,②y=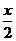 ,③y=-x-1 ,④xy=2,
⑤y=
,③y=-x-1 ,④xy=2,
⑤y=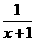 ,⑥y=
,⑥y=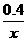 ,其中反比例函数有( )
,其中反比例函数有( )
A.3个 B.4个 C.5个 D.6个
4、(2007福建福州)如图12,已知直线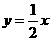 与双曲线
与双曲线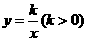 交于
交于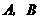 两点,且点
两点,且点 的横坐标为
的横坐标为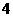 .
.
(1)求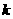 的值;
的值;
(2)若双曲线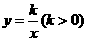 上一点
上一点 的纵坐标为8,求
的纵坐标为8,求 的面积;
的面积;
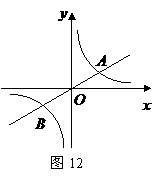 (3)过原点
(3)过原点 的另一条直线
的另一条直线 交双曲线
交双曲线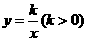 于
于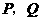 两点(
两点(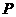 点在第一象限),若由点
点在第一象限),若由点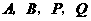 为顶点组成的四边形面积为
为顶点组成的四边形面积为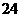 ,求点
,求点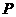 的坐标.
的坐标.
解:(1) 点
点 横坐标为
横坐标为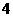 ,
, 当
当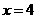 时,
时,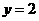 .
.
 点
点 的坐标为
的坐标为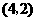 .
.
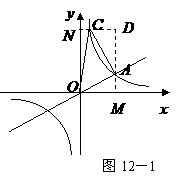
 点
点 是直线
是直线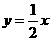 与双曲线
与双曲线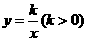 的交点,
的交点,
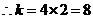 .
.
(2)解法一:如图12-1,
 点
点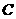 在双曲线上,当
在双曲线上,当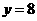 时,
时,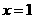
 点
点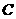 的坐标为
的坐标为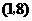 .
.
过点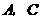 分别做
分别做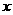 轴,
轴,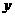 轴的垂线,垂足为
轴的垂线,垂足为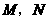 ,得矩形
,得矩形 .
.
 ,
,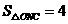 ,
,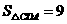 ,
, .
.
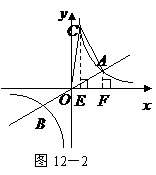
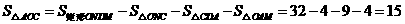 .
.
解法二:如图12-2,
过点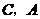 分别做
分别做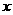 轴的垂线,垂足为
轴的垂线,垂足为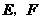 ,
,
 点
点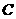 在双曲线
在双曲线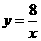 上,当
上,当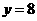 时,
时,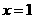 .
.
 点
点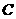 的坐标为
的坐标为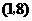 .
.
 点
点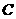 ,
, 都在双曲线
都在双曲线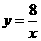 上,
上,
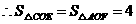
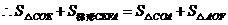 .
.
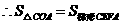 .
.
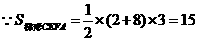 ,
,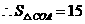 .
.
(3) 反比例函数图象是关于原点
反比例函数图象是关于原点 的中心对称图形,
的中心对称图形,
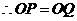 ,
,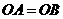 .
. 四边形
四边形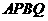 是平行四边形.
是平行四边形.
 .
.
设点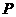 横坐标为
横坐标为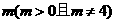 ,得
,得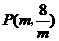 .
.
过点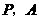 分别做
分别做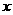 轴的垂线,垂足为
轴的垂线,垂足为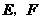 ,
,
 点
点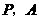 在双曲线上,
在双曲线上,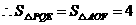 .
.
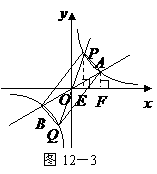
若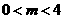 ,如图12-3,
,如图12-3,
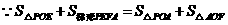 ,
,
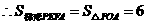 .
.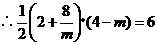 .
.
解得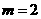 ,
,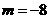 (舍去).
(舍去).
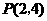 .
.
若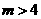 ,如图12-4,
,如图12-4,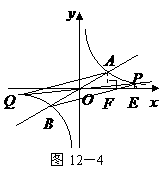
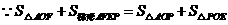 ,
,
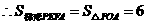 .
.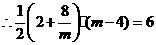 ,
,
解得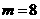 ,
,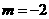 (舍去).
(舍去).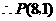 .
.
 点
点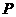 的坐标是
的坐标是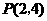 或
或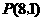 .
.
3、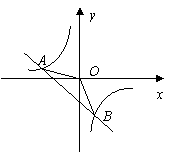 (2007四川成都)如图,一次函数
(2007四川成都)如图,一次函数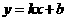 的图象与反比例函数
的图象与反比例函数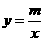 的图象交于
的图象交于 两点.
两点.
(1)试确定上述反比例函数和一次函数的表达式;
(2)求 的面积.
的面积.
解:(1) 点
点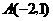 在反比例函数
在反比例函数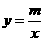 的图象上,
的图象上,
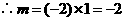 .
. 反比例函数的表达式为
反比例函数的表达式为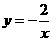 .
.
 点
点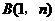 也在反比例函数
也在反比例函数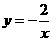 的图象上,
的图象上,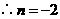 ,即
,即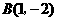 .
.
把点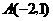 ,点
,点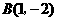 代入一次函数
代入一次函数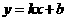 中,得
中,得
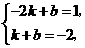 解得
解得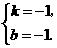
 一次函数的表达式为
一次函数的表达式为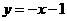 .
.
(2)在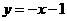 中,当
中,当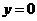 时,得
时,得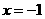 .
. 直线
直线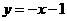 与
与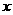 轴的交点为
轴的交点为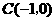 .
.
 线段
线段 将
将 分成
分成 和
和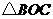 ,
,
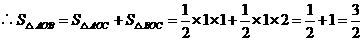 .
.
2、(2007四川乐山)从甲、乙两题中选做一题即可.如果两题都做,只以甲题计分.
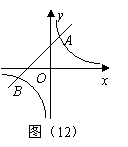 题甲:如图(12),反比例函数
题甲:如图(12),反比例函数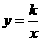 的图象与一次函数
的图象与一次函数 的图象交于
的图象交于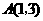 ,
,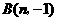 两点.
两点.
(1)求反比例函数与一次函数的解析式;
(2)根据图象回答:当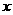 取何值时,反比例函数的值大于一次
取何值时,反比例函数的值大于一次
函数的值.
解:(1)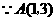 在
在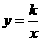 的图象上,
的图象上,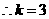 ,
,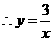
又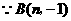 在
在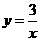 的图象上,
的图象上,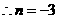 ,即
,即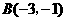
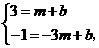 解得:
解得: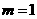 ,
,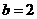 , 反比例函数的解析式为
, 反比例函数的解析式为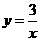 ,
,
一次函数的解析式为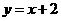 ,
,
(2)从图象上可知,当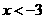 或
或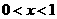 时,反比例函数的值大于一次函数的值
时,反比例函数的值大于一次函数的值
1、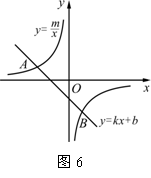 (2007四川资阳)如图6,已知A(-4,2)、B(n,-4)是一次函数y=kx+b的图象与反比例函数
(2007四川资阳)如图6,已知A(-4,2)、B(n,-4)是一次函数y=kx+b的图象与反比例函数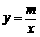 的图象的两个交点.
的图象的两个交点.
(1) 求此反比例函数和一次函数的解析式;
(2) 根据图象写出使一次函数的值小于反比例函数的值的x的取值范围.
解:(1) ∵ 点A(-4,2)和点B(n,-4)都在反比例函数y=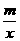 的图象上,
的图象上,
∴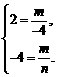 解得
解得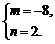
又由点A(-4,2)和点B(2,-4)都在一次函数y=kx+b的图象上,
∴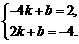 解得
解得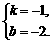
∴ 反比例函数的解析式为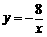 ,一次函数的解析式为y=-x-2 .
,一次函数的解析式为y=-x-2 .
(2) x的取值范围是x>2或-4<x<0 .
13、(2007广东梅州)近视眼镜的度数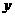 (度)与镜片焦距
(度)与镜片焦距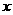 (米)成反比例,已知400度近视眼镜镜片的焦距为0.25米,则眼镜度数
(米)成反比例,已知400度近视眼镜镜片的焦距为0.25米,则眼镜度数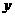 与镜片焦距
与镜片焦距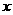 之间的函数关系式为
.
之间的函数关系式为
.
答: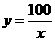
12、(2007江苏连云港)小明家离学校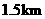 ,小明步行上学需
,小明步行上学需 ,那么小明步行速度
,那么小明步行速度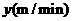 可以表示为
可以表示为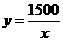 ;水平地面上重
;水平地面上重 的物体,与地面的接触面积为
的物体,与地面的接触面积为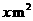 ,那么该物体对地面压强
,那么该物体对地面压强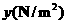 可以表示为
可以表示为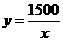 ;
; ,函数关系式
,函数关系式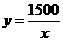 还可以表示许多不同情境中变量之间的关系,请你再列举1例: .
还可以表示许多不同情境中变量之间的关系,请你再列举1例: .
解:体积为1 500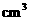 的圆柱底面积为
的圆柱底面积为 ,那么圆柱的高
,那么圆柱的高 可以表示为
可以表示为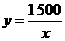 (其它列举正确均可);
(其它列举正确均可);
11、(2007陕西)在 的三个顶点
的三个顶点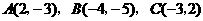 中,可能在反比例函数
中,可能在反比例函数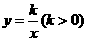 的图象上的点是
.B
的图象上的点是
.B
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com