2.一根蜡烛经凸透镜成一实像，物距u，像距v和凸透镜的焦距f满足关系式：+ = ．若u =12㎝，f =3㎝，则v的值为

A．8㎝　　　　 B．6㎝　　　 C．4㎝　　　 D．2㎝

1.计算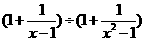的结果为.

A.1　　 　　　B.x+1　　 　　C.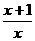　 　　D.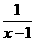

7．已知==,求　 的值

＊　　 8．化简　　

＊(9)＝求的值。

＊(10)设++＝，求证：a、b、c三个数中必有两个数之和为零。

5．已知m²－5m+1=o　　 求(1) m³+　　　　(2)m－的值

＊6。当x=1998,y=1999时，　　 求分式 的值　　　　　　

1．化简÷ · 　　

＊2．当a=时，求分式(－ +1) ÷的值

＊3．化简 　　　　　　4。已知 += 值,求+的值

8．化简下列各式:

(1)　+－　　　　　　　　(2)　(xy+y²)÷ ·　　　　　　　　　　　　　　　

＊(3)　[1－(a－)²÷ ]·　　

(4)　若(–1)a=1，求 －+1的值

(5) 已知 x²－5xy+6y²=0　 求 的值

独立训练　　　　　　 　　　

7．若x >y>0,则－ 的结果是(　 )

(A)　 0　 (B)正数　　 (C)　 负数　　 (D) 以上情况都有可能

8、如图，在直角坐标系中，O是原点，A、B、C三点的坐标分别为A(18，0)，B(18，6)，C(8，6)，四边形OABC是梯形，点P、Q同时从原点出发，分别坐匀速运动，其中点P沿OA向终点A运动，速度为每秒1个单位，点Q沿OC、CB向终点B运动，当这两点有一点到达自己的终点时，另一点也停止运动。

　　 ⑴ 求出直线OC的解析式及经过O、A、C三点的抛物线的解析式。

⑵ 试在⑴中的抛物线上找一点D，使得以O、A、D为顶点的三角形与△AOC全等，请直接写出点D的坐标。

⑶ 设从出发起，运动了t秒。如果点Q的速度为每秒2个单位，试写出点Q的坐标，并写出此时t的取值范围。

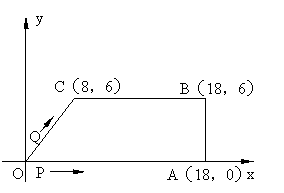⑷ 设从出发起，运动了t秒。当P、Q两点运动的路程之和恰好等于梯形OABC的周长的一半，这时，直线PQ能否把梯形的面积也分成相等的两部分，如有可能，请求出t的值；如不可能，请说明理由。

7、如图，已知矩形ABCD的边长AB=2，BC=3，点P是AD边上的一动点(P异于A、D)，Q是BC边上的任意一点. 连AQ、DQ，过P作PE∥DQ交AQ于E，作PF∥AQ交DQ于F.

(1)求证：△APE∽△ADQ；

(2)设AP的长为x，试求△PEF的面积S_△PEF关于x的函数关系式，并求当P在何处时，S_△PEF取得最大值？最大值为多少？

(3)当Q在何处时，△ADQ的周长最小？(须给出确定Q在何处的过程或方法，不必给出证明)

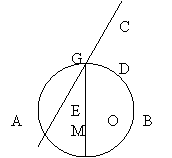
6．已知抛物线y=-x²-2kx+3k²(k>0)交x轴于A、B两点,交y轴于点C,以AB 为直径的⊙E交y轴于点D、F(如图),且DF=4,G 是劣弧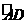上的动点(不与点A、D重合),直线CG交x轴于点P.

(1)　　 求抛物线的解析式;

(2)　　 当直线 CG是⊙E的切线时,求tan∠PCO的值.

(3)