
题目列表(包括答案和解析)
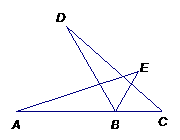
4、如图,AB=DB,BC=BE,要使△AEB≌△DCB,
则需增加的条件是( )
A ∠A=∠D B ∠E=∠C
C ∠A=∠C D ∠ABE=∠DBC
3、能判定两个三角形全等的是( )
A ∠A=∠A′,∠B=∠B′,∠C=∠C′ B BC=B′C′,AC=A′C′,∠B=∠B′
 C AC=A′C′,∠A=∠A′,∠B=∠B′ D ∠A=∠A′,∠B=∠C′,AC=A′C′
C AC=A′C′,∠A=∠A′,∠B=∠B′ D ∠A=∠A′,∠B=∠C′,AC=A′C′
2、、下列条件中,能判定△ABC≌△DEF的是( )
A AB=DE,BC=EF, ∠A=∠D B ∠A=∠D, ∠C=∠F,AC=EF
C ∠B=∠E,∠A=∠D,AC=EF D AB=DE,BC=EF, △ABC的周长等于△DEF的周长
5、三角形的面积
(1)一般三角形:S= (h是a边上的高)
(2)直角三角形:S= = (a,b是直角边,c是斜边,h是斜边上的高)
(3)等边三角形:S= (a是边长)
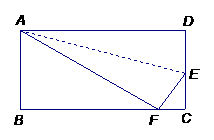
例1、 折叠长方形的一边AD,使点D落在BC边上的点F处,已知AB=8cm,
BC=10cm,求CE的长。
分析: AFE是
AFE是 ADE翻折得到的,则
ADE翻折得到的,则 AFE
AFE
 ADE
ADE
习题1、如果 ABC∽
ABC∽
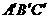 ,相似比k=1∶2,
,相似比k=1∶2,
 ABC与
ABC与
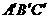 的周长比为
;
的周长比为
; ABC与
ABC与
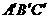 的对应高线比为 ;
的对应高线比为 ;
 ABC与
ABC与
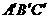 的对应边的中线比为
;
的对应边的中线比为
;

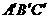 与
与 ABC的对应角的角平分线比为
;
ABC的对应角的角平分线比为
;
 ABC与
ABC与
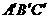 的面积比为 。
的面积比为 。
4、全等三角形
全等三角形对应边 ,对应角 ;对应边、对应中线、对应高、对应角平分线 ; 全等三角形的周长、面积 。
一般三角形全等的判定(如图)
(1) 边角边(SSS)
∵AB=A′B′ BC=B′C ′ _______=_____∴△ABC≌△A′B′C′
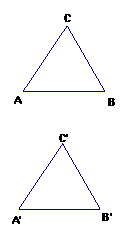 (2)边角边(SAS)
(2)边角边(SAS)
∵AB=A′B′ ∠B=∠B′ _______=_____
∴△ABC≌△A′B′C′
(3) 角边角(ASA)
 ∠B=∠B′ ____=_____ ∠C=∠C′ ∴△ABC≌△A′B′C′
∠B=∠B′ ____=_____ ∠C=∠C′ ∴△ABC≌△A′B′C′
(4) 角角边(AAS)
∵∠A=∠A′ ∠C=∠C′ _______=_____
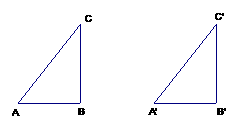 ∴△ABC≌△A′B′C′
∴△ABC≌△A′B′C′
直角三角形全等的判定:
斜边直角边定理( )
 AB=A′B′ _____=_____
AB=A′B′ _____=_____
∴Rt△ABC≌Rt△A′B′C′
3、相似三角形
(1)相似三角形的性质
相似三角形的对应边 ,对应角 。
对应高的比、对应角平分线的比、对应中线的比、对应周长的比都等于 比。
对应面积的比等于 。
(2)相似三角形的识别方法:
①如果两个三角形 角对应 ,那么这两个三角形相似。
②如果两个三角形 边对应 ,那么这两个三角形相似。
③如果两个三角形 边对应 ,且 ,那么这两个三角形相似。
2、特殊的三角形
等腰三角形
(1)等腰三角形的两个底角 ,简写成:等边对 。
(2)等腰三角形的顶角 、底边上的 、底边上的高 。
(3)如果一个三角形有两个角相等,那么这两个角所对的 也相等,
简写成:等角对 。
如果一个三角形有两条边相等,那么这两条边所对的 也相等,
简写成:等边对 。
(4)三个角相等的三角形是 三角形。
(5)有一个角等于60°的等腰三角形是 三角形。
直角三角形
(1)直角三角形两锐角 。
(2)在直角三角形中,30°角所对的直角边等于斜边的 。
(3)勾股定理:
在Rt ABC中,
ABC中,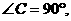 AB=a, BC=b, AC=c,则a,b,c满足关系:
AB=a, BC=b, AC=c,则a,b,c满足关系:
a= ,b= ,c=
在Rt ABC中,
ABC中,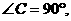 AB=5,BC=4,则AC= .
AB=5,BC=4,则AC= .
在Rt ABC中,
ABC中,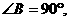 AB=4,BC=3,则AC= .
AB=4,BC=3,则AC= .
在Rt ABC中,
ABC中,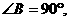 AB=1,AC=2,则BC= .
AB=1,AC=2,则BC= .
 (4)勾股定理逆定理:如果三角形三边为a,b,c,满足
,那么这个三角形为直角三角形。
(4)勾股定理逆定理:如果三角形三边为a,b,c,满足
,那么这个三角形为直角三角形。
(5)直角三角形斜边上的中线等于 。
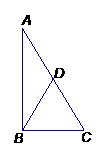
在Rt ABC中,
ABC中, 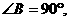 D是AC边的中点,
D是AC边的中点,
已知AC=4,则BD=
1、三角形基本概念
(1)三边关系:
三角形任意两边之和 第三边,三角形任意两边之差 第三边。
(2)三角形内角和定理:三角形的三个内角和等于 。
(3)外角性质:三角形的一个外角等于和它 的两内角的和。
三角形的一个外角大于任何一个和它 的内角。(填“不相邻”或“相邻”)
(4)角平分线:OC是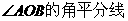 ,则∠ =∠ =
,则∠ =∠ =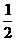 ∠
∠
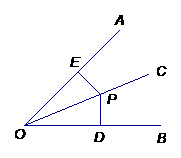 角平分线定理:角平分线上的点到 的两边的距离
。
角平分线定理:角平分线上的点到 的两边的距离
。
OC是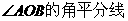 ,P是OC上一点,
,P是OC上一点,
PE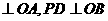 ,则
=
,则
=
 (5)线段垂直平分线定理:
(5)线段垂直平分线定理:
线段垂直平分线上的点到这条线段 的距离 。
直线CD是线段AB的垂直平分线,P是CD上一点,
O是垂足,则 = , =
(6)三角形的三条角平分线相交于一点( 心);
三条边的垂直平分线相交于一点( 心)。
(7)中位线:三角形的中位线 第三边,并且等于 。
5.如图是某段河床横断面的示意图.查阅该河段水文资料,得到下表中的数据
|
x/m |
5 |
10 |
20 |
30 |
40 |
 50 50 |
|
y/m |
0.125 |
0.5 |
2 |
4.5 |
8 |
12.5 |
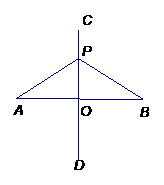
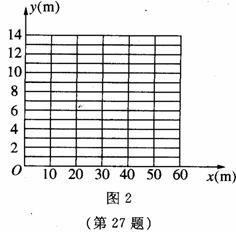
请你以上表中的各对数据(x,y)作为点的坐标,尝试在坐标系中
画出y关于x的函数图象.
 (2)1填写下表
(2)1填写下表
|
x |
5 |
10 |
20 |
30 |
40 |
50 |
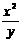 |
|
|
|
|
|
|
2根据所填表中数据呈现的规律,猜想出用x表示
y的二次函数的表达式: .
3当水面宽度为36m时,一艘吃水深度(船底部到
水面的距离)为1.8m的货船能否在这个河段安全通过?
为什么?
4.心理学家研究发现,一般情况下, 学生的注意力随着老师讲课时间的变化而变化,讲课开始时,学生的注意力逐步增强, 中间有一段时间学生的注意力保持较为理想的状态,随后学生的注意力开始分散.经过实验分析可知, 学生的注意力y随时间t(分钟)的变化规律有如下关系式: 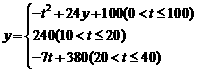 (y值越大表示接受能力越强)
(y值越大表示接受能力越强)
(1)讲课开始后第5分钟时与讲课开始后第25分钟时比较, 何时学生的注意力更集中?
(2)讲课开始后多少分钟,学生的注意力最集中?能持续多少分钟?
(3)一道数学难题,需要讲解24分钟,为了效果较好,要求学生的注意力最低达到180,那么经过适当安排,老师能否在学生注意力达到所需的状态下讲解完这道题目?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com