
题目列表(包括答案和解析)
5.函数y=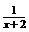 中,自变量x的取值范围是___________________;
中,自变量x的取值范围是___________________;
函数y=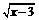 中,自变量x的取值范围是___________________.
中,自变量x的取值范围是___________________.
4. 分解因式:x2-4=_________________.
分解因式:x2-4=_________________.
3.据中新社报道:2010年我国粮食产量将达到540 000 000 000千克,这个粮食产量用科学记数法可表示为______________________千克.
2.4的算术平方根是__________,-8的立方根是___________.
1.3的相反数是_________,-2的绝对值是___________.
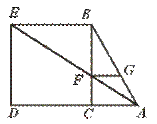
30.已知:如图,在△ABC中,∠C=90°,以BC为边向外作正方形BEDC,连结AE交BC于F,作FG∥BE交AB于G.
求证:FG=FC.
[提示]证明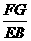 =
=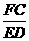 .
.
[答案]∵ FG∥BE,∴ 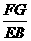 =
=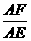 .∵ FC∥ED,∴
.∵ FC∥ED,∴ 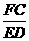 =
=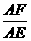 .
.
∴ 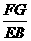 =
=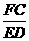 .又 EB=ED,∴ FG=FC.
.又 EB=ED,∴ FG=FC.
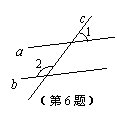
29.如图,BD、CE为△ABC的高,求证∠AED=∠ACB.
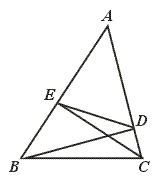
[提示]先证△ABD∽△ACE,再证△ADE∽△ABC.
[答案]∵ ∠ADB=∠AEC=90°,∠A=∠A,
∴ △ABD∽△ACE.∴ 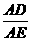 =
=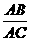 .
.
又 ∠A=∠A,∴ △ADE∽△ABC.∴ ∠AED=∠ACB.
[点评]本题要求运用相似三角形的判定与性质.
28.已知:如图,△ABC中,AB=AC,AD是中线,P是AD上一点,过C作CF∥AB,延长BP交AC于E,交CF于F.求证:BP2=PE·PF.
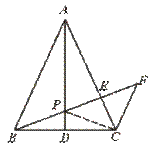
[提示]先证PB=PC,再证△EPC∽△CPF.
[答案]连结PC.
∵ AB=AC,AD是中线,∴ AD是△ABC的对称轴.
∴ PC=PB,∠PCE=∠ABP.∵ CF∥AB,
∴ ∠PFC=∠ABP.∴ ∠PCE=∠PFC.
又 ∠CPE=∠EPC,∴ △EPG∽△CPF.
∴ 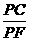 =
=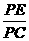 .即 PC2=PE·PF.∴ BP2=PE·PF.
.即 PC2=PE·PF.∴ BP2=PE·PF.
[点评]本题要求运用等腰三角形的性质以及相似三角形的判定与性质.
27.已知:如图,在正方形ABCD中,P是BC上的点,且BP=3PC,Q是CD的中点.求证:△ADQ∽△QCP.
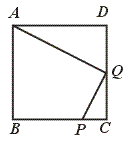
[提示]先证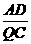 =
=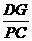 .
.
[答案]在正方形ABCD中,
∵ Q是CD的中点,∴ 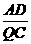 =2.
=2.
∵ 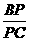 =3,∴
=3,∴ 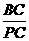 =4.
=4.
又 BC=2DQ,∴ 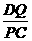 =2.
=2.
在△ADQ和△QCP中,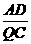 =
=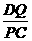 ,∠C=∠D=90°,
,∠C=∠D=90°,
∴ △ADQ∽△QCP.
[点评]本题要求运用相似三角形的判定定理.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com