
题目列表(包括答案和解析)
8、(2007鄂尔多斯)我们给出如下定义:若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称这个四边形为勾股四边形,这两条相邻的边称为这个四边形的勾股边.
(1)写出你所学过的特殊四边形中是勾股四边形的两种图形的名称_________,________;
(2)如图16(1),已知格点(小正方形的顶点)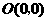 ,
,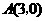 ,
,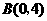 ,请你画出以格点为顶点,
,请你画出以格点为顶点,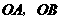 为勾股边且对角线相等的勾股四边形
为勾股边且对角线相等的勾股四边形 ;
;

(3)如图16(2),将 绕顶点
绕顶点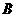 按顺时针方向旋转
按顺时针方向旋转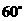 ,得到
,得到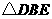 ,连结
,连结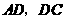 ,
,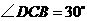 .
.
 求证:
求证: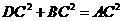 ,即四边形
,即四边形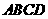 是勾股四边形.
是勾股四边形.
解:
(1)正方形、长方形、直角梯形.(任选两个均可)················ 2分(填正确一个得1分)
 (2)答案如图所示.
(2)答案如图所示.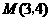 或
或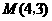 .(没有写出不扣分)
.(没有写出不扣分)
····································································· 2分(根据图形给分,一个图形正确得1分)

(3)证明:连结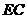
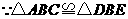 ····································································································· 5分
····································································································· 5分
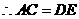 ,
,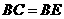 ······························································································ 6分
······························································································ 6分
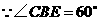
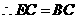 ,
,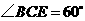 ······························································· 7分
······························································· 7分


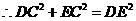 ·············································· 8分
·············································· 8分
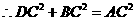 ,即四边形
,即四边形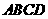 是勾股四边形················································· 9分
是勾股四边形················································· 9分
7、(2007江苏无锡)图1是由若干个小圆圈堆成的一个形如正三角形的图案,最上面一层有一个圆圈,以下各层均比上一层多一个圆圈,一共堆了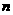 层.将图1倒置后与原图1拼成图2的形状,这样我们可以算出图1中所有圆圈的个数为
层.将图1倒置后与原图1拼成图2的形状,这样我们可以算出图1中所有圆圈的个数为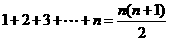 .
.
 图1 图2 图3 图4
图1 图2 图3 图4
如果图1中的圆圈共有12层,(1)我们自上往下,在每个圆圈中都按图3的方式填上一串连续的正整数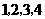
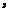
 ,则最底层最左边这个圆圈中的数是 ;(2)我们自上往下,在每个圆圈中都按图4的方式填上一串连续的整数
,则最底层最左边这个圆圈中的数是 ;(2)我们自上往下,在每个圆圈中都按图4的方式填上一串连续的整数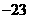 ,
,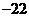 ,
,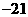 ,
, ,求图4中所有圆圈中各数的绝对值之和.
,求图4中所有圆圈中各数的绝对值之和.
解:(1)67.·············································································································· 2分
(2)图4中所有圆圈中共有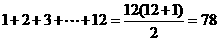 个数,
个数,
其中23个负数,1个0,54个正数,············································································· 4分
 图4中所有圆圈中各数的绝对值之和
图4中所有圆圈中各数的绝对值之和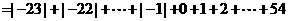
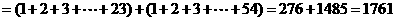 .······························· 6分
.······························· 6分
4、(2007江苏连云港)如图1,点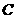 将线段
将线段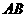 分成两部分,如果
分成两部分,如果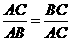 ,那么称点
,那么称点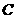 为线段
为线段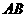 的黄金分割点.
的黄金分割点.
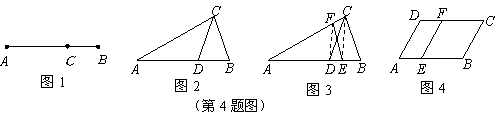
某研究小组在进行课题学习时,由黄金分割点联想到“黄金分割线”,类似地给出“黄金分割线”的定义:直线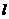 将一个面积为
将一个面积为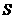 的图形分成两部分,这两部分的面积分别为
的图形分成两部分,这两部分的面积分别为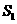 ,
,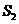 ,如果
,如果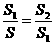 ,那么称直线
,那么称直线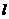 为该图形的黄金分割线.
为该图形的黄金分割线.
(1)研究小组猜想:在 中,若点
中,若点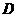 为
为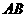 边上的黄金分割点(如图2),则直线
边上的黄金分割点(如图2),则直线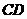 是
是 的黄金分割线.你认为对吗?为什么?
的黄金分割线.你认为对吗?为什么?
(2)请你说明:三角形的中线是否也是该三角形的黄金分割线?
(3)研究小组在进一步探究中发现:过点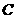 任作一条直线交
任作一条直线交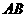 于点
于点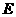 ,再过点
,再过点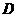 作直线
作直线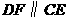 ,交
,交 于点
于点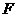 ,连接
,连接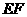 (如图3),则直线
(如图3),则直线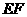 也是
也是 的黄金分割线.
的黄金分割线.
请你说明理由.
(4)如图4,点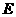 是
是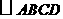 的边
的边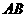 的黄金分割点,过点
的黄金分割点,过点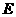 作
作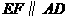 ,交
,交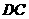 于点
于点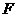 ,显然直线
,显然直线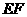 是
是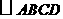 的黄金分割线.请你画一条
的黄金分割线.请你画一条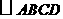 的黄金分割线,使它不经过
的黄金分割线,使它不经过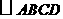 各边黄金分割点.
各边黄金分割点.
解:(1)直线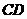 是
是 的黄金分割线.理由如下:
的黄金分割线.理由如下:
设 的边
的边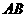 上的高为
上的高为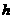 .
.
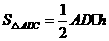 ,
,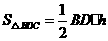 ,
,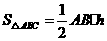 ,
,
所以,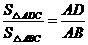 ,
,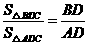 .······················································ 2分
.······················································ 2分
又因为点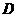 为边
为边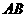 的黄金分割点,所以有
的黄金分割点,所以有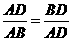 .因此
.因此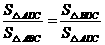 .
.
所以,直线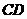 是
是 的黄金分割线.·················································· 4分
的黄金分割线.·················································· 4分
(2)因为三角形的中线将三角形分成面积相等的两部分,此时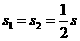 ,即
,即
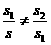 ,所以三角形的中线不可能是该三角形的黄金分割线.··············· 6分
,所以三角形的中线不可能是该三角形的黄金分割线.··············· 6分
(3)因为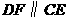 ,所以
,所以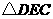 和
和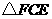 的公共边
的公共边 上的高也相等,
上的高也相等,
所以有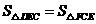 .·········································································· 7分
.·········································································· 7分
设直线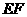 与
与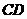 交于点
交于点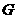 .所以
.所以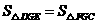 .
.
所以
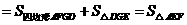 ,
,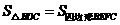 .
.
又因为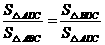 ,所以
,所以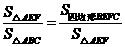 .······························ 9分
.······························ 9分
因此,直线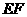 也是
也是 的黄金分割线.·········································· 10分
的黄金分割线.·········································· 10分
(4)画法不惟一,现提供两种画法;····················································· 12分
画法一:如答图1,取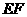 的中点
的中点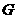 ,再过点
,再过点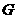 作一条直线分别交
作一条直线分别交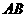 ,
,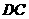 于
于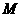 ,
,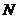 点,则直线
点,则直线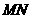 就是
就是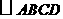 的黄金分割线.
的黄金分割线.
画法二:如答图2,在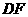 上取一点
上取一点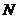 ,连接
,连接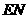 ,再过点
,再过点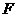 作
作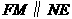 交
交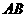 于点
于点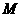 ,连接
,连接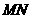 ,则直线
,则直线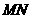 就是
就是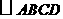 的黄金分割线.
的黄金分割线.


3、(2007广东梅州)将4个数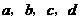 排成2行、2列,两边各加一条竖直线记成
排成2行、2列,两边各加一条竖直线记成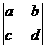 ,定义
,定义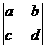
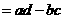 ,上述记号就叫做2阶行列式.若
,上述记号就叫做2阶行列式.若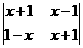
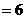 ,则
,则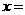 __________.
__________.
答: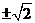
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com