
题目列表(包括答案和解析)
2.具备解决问题的基本策略和多样策略,具有实践能力和创新精神。
这一目标主要包括让学生尝试寻找不同的解决问题方法,评价
不同方法之间的差异,从不同的角度去认识同一个问题。
1. 能够从数学的角度提出问题、理解问题。
这一目标主要包括能够从日常生活中“看到”一些数学现象,并从数学现象、其它学科中的问题中发现数学关系或数学问题,能够综合运用相关的数学知识、方法去解决一些问题。
问题1 如图所示,用同样规格的黑、白两色正方形瓷砖铺设矩形地面,如下图所示:第n个图形中需用黑色瓷砖 块.(用含n的代数式表示)
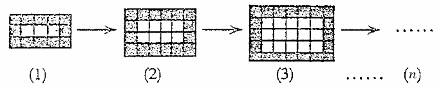
说明:本题是一个探索规律的问题,其所考查的正是基于归纳方法的合情推理活动能力。
问题2 小明骑自行车上学,开始以正常速度匀速行驶,但行至中途自行车出了故障,只好停下来修车。车修好后,因怕耽误上课,他比修车前加快了骑车速度继续匀速行驶。下面是行驶路程S(米)关于时间t(分)的函数图像,那么符合这个同学行驶情况的图像大致是------( )
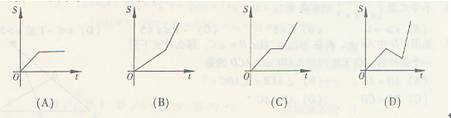
说明:本题是一个种较为新颖的推理题,推断是用图像表达的信息与用文字表达的相关信息之间的一致性。因此,它是考查基于文字信息和图像信息理解基础之上的推理能力,而不是我们所熟悉的几何证明能力。
问题3. 已知:如图,E、F、G、H按照AE=CG,BF=DH,BF=nAE(n是正整数)的关系,分别在两条邻边长为a、na的矩形ABCD各边上运动。设AE=x,四边形EFGH的面积为S。
(1)当n=1,2时,如图,观察运动情况,写出四边形EFGH各顶点运动到什么位置时,S=1/2S(矩形ABCD);
(2)当n=3时,如图,求S与x之间的函数关系式(写出自变量x的取值范围),探索S随x增大而变化的规律;猜想四边形EFGH各顶点运动到何位置,使S=1/2S(矩形ABCD);
(3)当n=k(k>=1)时,你所发现的规律和猜想是否成立?请说明理由。
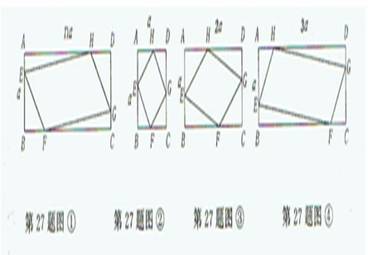
说明:本题是让学生寻找存在于图形的运动变化过程中的数学规律。关注的是推理活动,特别是合情推理(依据动点的变化特征、有关n的表达式的特点等,概括出其中的数量关系及其变化趋势),而不仅仅是数学证明、更不仅仅是几何证明。
问题4要判断如图△ABC的面积是△PBC面积的几倍,只用一把仅有刻度的直尺,需要度量的次数最少是------( )。
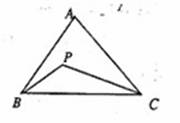
说明:本题采用了一个全新的形式来考查学生的推理能力。因为其求解过程实际上就是一个推理过程--借助面积公式,做适当的数学运算(就是推理!),获得最少的度量次数。
40、 以给定的图形“○○、△△、=”(两个圆、两个三角形、两条平行线)为构件,构思出独特且有意义的图形。举例:如图,右图中是符合要求的一个图形,你能构思出其它的图形吗?请在右框中画出与之不同的一个图形,并写出一句贴切、诙谐的解说词。
以给定的图形“○○、△△、=”(两个圆、两个三角形、两条平行线)为构件,构思出独特且有意义的图形。举例:如图,右图中是符合要求的一个图形,你能构思出其它的图形吗?请在右框中画出与之不同的一个图形,并写出一句贴切、诙谐的解说词。
39、读一读,想一想,做一做:
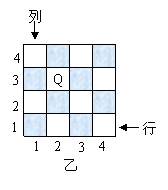
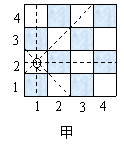
国际象棋、中国象棋和围棋号称为世界三大棋种.国际象棋中的“皇后”的威力可比中国象棋中的“车”大得多:“皇后”不仅能控制她所在的行与列中的每一个小方格,而且还能控制“斜”方向的两条直线上的每一个小方格.如图甲是一个4×4的小方格棋盘,图中的“皇后Q”能控制图中虚线所经过的每一个小方格.
① 在如图乙的小方格棋盘中有一“皇后Q”,她所在的位置可用“(2,3)”来表示,请说明“皇后Q”所在的位置“(2,3)”的意义,并用这种表示法分别写出棋盘中不能被该“皇后Q”所控制的四个位置.
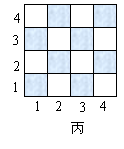
②如图丙也是一个4×4的小方格棋盘,请在这个棋盘中放入四个“皇后Q”,使这四个“皇后Q”之间互不受对方控制(在图丙中的某四个小方格中标出字母Q即可).
38、 如图是一块长方形ABCD的场地,长AB=102m,
如图是一块长方形ABCD的场地,长AB=102m,
宽AD=51m,从A、B两处入口的中路宽都为1m,
两小路汇合处路宽为2m,其余部分种植草坪,则
草坪面积为( )
(A)5050m2 (B)4900m2 (C)5000m2(D)4998m2
37、水平放置的正方体的六个面分别用“前面、后面、上面、
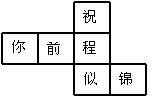 下面、左面、右面”表示.如右图,是一个正方体的平面展开图,
下面、左面、右面”表示.如右图,是一个正方体的平面展开图,
若图中的“似”表示正方体的前面, “锦”表示右面,
“程”表示下面.则“祝”、 “你”、
“前”分别表示正方体的___________________.
36、观察图形:图中是边长为1,2,3 …的正方形:当边长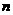 =1时,正方形被分成2个大小相等的小等腰直角三角形;当边长
=1时,正方形被分成2个大小相等的小等腰直角三角形;当边长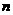 =2时,正方形被分成8个大小相等的小等腰直角三角形;当边长
=2时,正方形被分成8个大小相等的小等腰直角三角形;当边长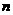 =3时,正方形被分成18个大小相等的小等腰直角三角形;以此类推:当边长为
=3时,正方形被分成18个大小相等的小等腰直角三角形;以此类推:当边长为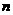 时,正方形被分成大小相等的小等腰直角三角形的个数是
。
时,正方形被分成大小相等的小等腰直角三角形的个数是
。
35、将一张长方形的纸对折,如图5所示可得到一条折痕(图中虚线). 继续对折,对折时每次折痕与上次的折痕保持平行,连续对折三次后,可以得到7条折痕,那么对折四次可以得到 条折痕 .如果对折n次,可以得到 _____________条折痕 。

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com