
题目列表(包括答案和解析)
3.与3x-6<0同解的不等式为( )
A.6>3x B.x>2 C.3x≤6 D.3x>6
2.在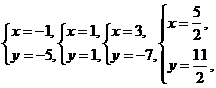 四对数值中,满足方程3x-y=2的有( )
四对数值中,满足方程3x-y=2的有( )
A.1对 B.2对 C.3对 D.4对
1.不等式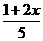 ≤1的解集在数轴上(图3-1)表示正确的是( )
≤1的解集在数轴上(图3-1)表示正确的是( )
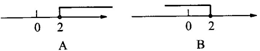
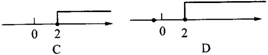
18、解:(1)由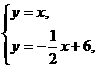 可得
可得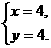 ∴A(4,4)。
∴A(4,4)。
(2)点P在y = x上,OP = t,则点P坐标为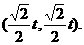
点Q的纵坐标为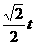 ,并且点Q在
,并且点Q在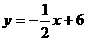 上。
上。
∴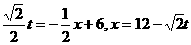 ,即点Q坐标为
,即点Q坐标为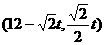 。
。
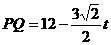 。 当
。 当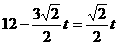 时,
时,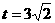 。当
。当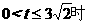 ,
,
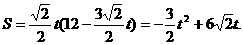 当点P到达A点时,
当点P到达A点时,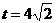 ,
,
当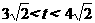 时,
时,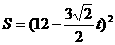
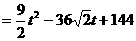 。
。
(3)有最大值,最大值应在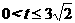 中,
中,
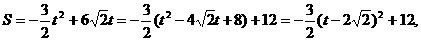
当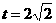 时,S的最大值为12。 (8分)
时,S的最大值为12。 (8分)
(4)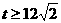 。
(10分)
。
(10分)
16、解:(1)解法一: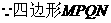 是矩形,
是矩形,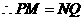 …………(1分)
…………(1分)

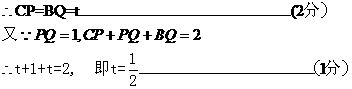
解法二: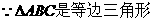 ,
,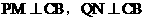
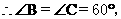
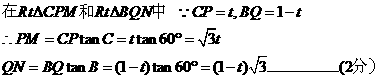
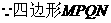 是矩形,
是矩形, 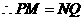 …………………(1分)
…………………(1分)
即: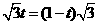 解得:
解得: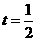
(2)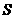 是定值,同(1)中解法二有:
是定值,同(1)中解法二有: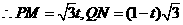
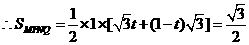 ……………………………(2分)
……………………………(2分)
(3)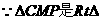 ,且
,且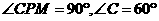 ,
, 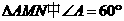
若使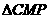 与
与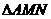 相似,对应的顶点只能是:
相似,对应的顶点只能是:
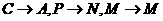 或
或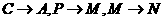 …………(1分)
…………(1分)
①当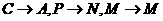 时,由
时,由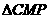 ∽
∽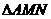 得:
得: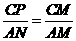
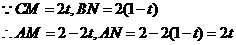
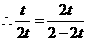 解得:
解得: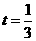 ………………………………(1分)
………………………………(1分)
②当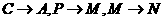 时,由
时,由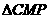 ∽
∽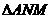 得:
得: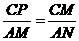
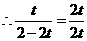 解得:
解得: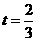 综合,所求的
综合,所求的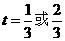 。
。
当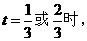 都有
都有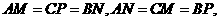
且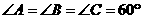

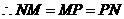 即
即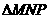 是等边三角形。
是等边三角形。
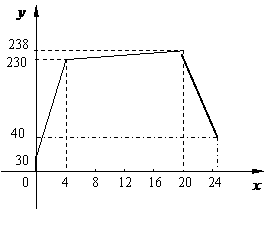
15、解:(1)根据图形:0∶00-20∶00之间气站每小时增加的储气量为:
(238-30)÷20=10.4(米3/小时)……………………(3分)
(2)设气站每小时进气量为 米3,每小时供气量为
米3,每小时供气量为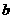 米3,
米3,
根据题意,得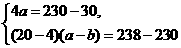 解得:
解得: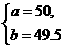 ………(1分)
………(1分)
 在20∶00-24∶00只打开供气阀门,到24:00时,气站的储气量为
在20∶00-24∶00只打开供气阀门,到24:00时,气站的储气量为
238-4×49.5=40,即当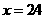 时,
时,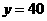 ;
;
又当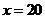 时,
时,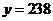 …………………(1分)
…………………(1分)
设20∶00-24∶00时,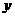 与
与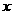 的函数关系式为
的函数关系式为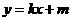 ,
,
则 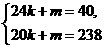 解得:
解得: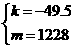 所以,
所以,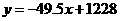
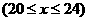 图形如图所示
图形如图所示
(3)68小时, 258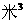 ……………………………………(4分)
……………………………………(4分)
比较3种情况的最大值。
14、(1)路程每填对一个得1分,运输费用每填对一个得0.5分。
|
|
路 程 (单位:千米) |
运输单价 (元/吨·千米) |
数 量 (单位:吨) |
运输费用 (单位:元) |
|
铁路AC |
120 |
1.2 |
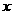 |
144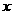 |
|
公路CD |
10 |
1.5 |
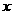 |
15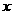 |
|
铁路DE |
110 |
1.2 |
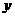 |
132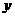 |
|
公路EB |
20 |
1.5 |
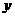 |
30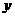 |
(2)根据题意得: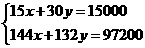 解得:
解得: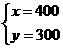
因此,这批产品全部销售后获得的利润为
300×8000-400×1000-15000-97200=1887800(元)……………(2分)
20.(08山西太原)已知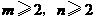 ,且
,且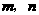 均为正整数,
均为正整数,
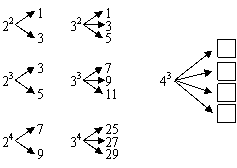 如果将
如果将 进行如下方式的“分解”,那么下列三个叙述:
进行如下方式的“分解”,那么下列三个叙述:
(1)在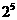 的“分解”中最大的数是11.
的“分解”中最大的数是11.
(2)在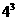 的“分解”中最小的数是13.
的“分解”中最小的数是13.
(3)若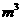 的“分解”中最小的数是23,则
的“分解”中最小的数是23,则 等于5.
等于5.
其中正确的是 .(2)
17.(08山西太原)抛物线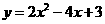 的顶点坐标是 .(1,1)
的顶点坐标是 .(1,1)
14.(08山西太原)在市政府与国家开发银行山西省分行举行的“百校兴学”工程金融合作签约仪式上,首批项目申请银行贷款3.16亿元.用科学记数法表示3.16亿的结果是 .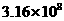
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com