
题目列表(包括答案和解析)
25、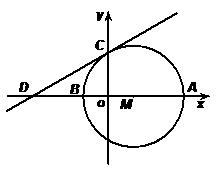 如图,在直角坐标系中,以点M(3,0)为圆心,以6为半径的圆分别交x轴的正半轴于点A,交x轴的负半轴交于点B,交y轴的正半轴于点C ,过点C的直线交x轴的负半轴于点D(-9,0)
如图,在直角坐标系中,以点M(3,0)为圆心,以6为半径的圆分别交x轴的正半轴于点A,交x轴的负半轴交于点B,交y轴的正半轴于点C ,过点C的直线交x轴的负半轴于点D(-9,0)
(1) 求A、C两点的坐标;
(2) 求证 直线CD是⊙M的切线‘
(3) 若抛物线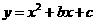 经过M、A两点,求此抛物线的解析式;
经过M、A两点,求此抛物线的解析式;
24、已知:如图,AB是⊙O的直径,点P是AB延长线上一点,PC切⊙O于点C,在射线PA上截取PD=PC,连接CD,并延长交⊙O于点E.
(1)求证:∠ABE=∠BCE;
(2)当点P在AB的延长线上运动时,判断sin∠BCE的值是否随点P位置的变化而变化,提出你的猜想并加以证明.
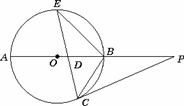
23、如图,⊙O的直径AB=6cm,D为⊙O上一点,∠BAD=30°,过点D的切线交AB的延长线于点C.求∠ADC的度数及AC的长.
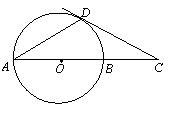
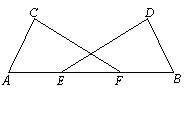
22、如图,已知∠A=∠B,AE=EF=FB,AC=BD.求证:CF=DE.
21、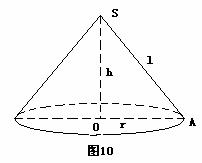 已知圆锥的底面半径为r=20cm,高h=
已知圆锥的底面半径为r=20cm,高h=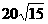 cm,现在有一只蚂蚁从底边上一点A出发。在侧面上爬行一周又回到A点,求蚂蚁爬行的最短距离。
cm,现在有一只蚂蚁从底边上一点A出发。在侧面上爬行一周又回到A点,求蚂蚁爬行的最短距离。
20、 观察下面的点阵图,探究其中的规律。摆第1个“小屋子”需要5个点,摆第2个“小屋子”需要
个点,摆第3个“小屋子”需要
个点?(1)、摆第10个这样的“小屋子”需要多少个点?
观察下面的点阵图,探究其中的规律。摆第1个“小屋子”需要5个点,摆第2个“小屋子”需要
个点,摆第3个“小屋子”需要
个点?(1)、摆第10个这样的“小屋子”需要多少个点?
(2)、写出摆第n个这样的“小屋子”需要的总点数,S与n的关系式。
19、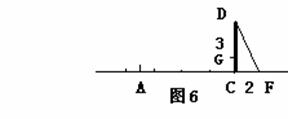 已知:CD为一幢3米高的温室,其南面窗户的底框G距地面1米,CD在地面上留下的最大影长CF为2米,现欲在距C点7米的正南方A点处建一幢12米高的楼房AB(设A,C,F在同一水平线上)
已知:CD为一幢3米高的温室,其南面窗户的底框G距地面1米,CD在地面上留下的最大影长CF为2米,现欲在距C点7米的正南方A点处建一幢12米高的楼房AB(设A,C,F在同一水平线上)
(1)、按比例较精确地作出高楼AB及它的最大影长AE;
(2)、问若大楼AB建成后是否影响温室CD的采光,试说明理由。
18、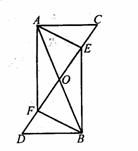 已知,如图,
已知,如图,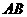 、
、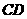 相交于点
相交于点 ,
, ∥
∥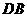 ,
, =
=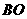 ,
,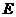 、
、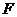 分别是
分别是 、
、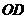 中点。求证:四边形
中点。求证:四边形 是平行四边形。
是平行四边形。
17、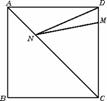 如图,正方形ABCD的边长为8,M在DC上,且DM=2,N是AC上一动点,求DN+MN的最小值.
如图,正方形ABCD的边长为8,M在DC上,且DM=2,N是AC上一动点,求DN+MN的最小值.
16、小明的身高是1.7 m,他的影长是2 m,同一时刻学校旗杆的影长是10 m,求旗杆的高。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com