
题目列表(包括答案和解析)
7.用待定系数法求二次函数的解析式
(1)一般式: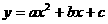 .已知图像上三点或三对
.已知图像上三点或三对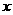 、
、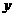 的值,通常选择一般式.
的值,通常选择一般式.
(2)顶点式: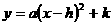 .已知图像的顶点或对称轴,通常选择顶点式.
.已知图像的顶点或对称轴,通常选择顶点式.
(3)交点式:已知图像与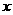 轴的交点坐标
轴的交点坐标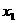 、
、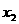 ,通常选用交点式:
,通常选用交点式: .
.
6.抛物线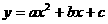 中,
中,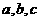 的作用
的作用
(1)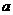 决定开口方向及开口大小,这与
决定开口方向及开口大小,这与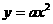 中的
中的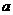 完全一样.
完全一样.
(2)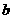 和
和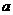 共同决定抛物线对称轴的位置.由于抛物线
共同决定抛物线对称轴的位置.由于抛物线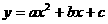 的对称轴是直线
的对称轴是直线
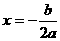 ,故:①
,故:①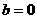 时,对称轴为
时,对称轴为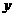 轴;②
轴;②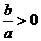 (即
(即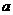 、
、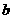 同号)时,对称轴在
同号)时,对称轴在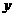 轴左侧;③
轴左侧;③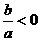 (即
(即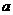 、
、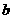 异号)时,对称轴在
异号)时,对称轴在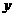 轴右侧.
轴右侧.
(3)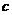 的大小决定抛物线
的大小决定抛物线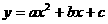 与
与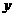 轴交点的位置.
轴交点的位置.
当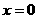 时,
时,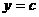 ,∴抛物线
,∴抛物线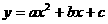 与
与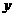 轴有且只有一个交点(0,
轴有且只有一个交点(0,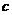 ):
):
①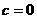 ,抛物线经过原点; ②
,抛物线经过原点; ②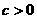 ,与
,与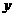 轴交于正半轴;③
轴交于正半轴;③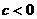 ,与
,与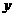 轴交于负半轴.
轴交于负半轴.
以上三点中,当结论和条件互换时,仍成立.如抛物线的对称轴在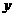 轴右侧,则
轴右侧,则 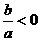 .
.
5.求抛物线的顶点、对称轴的方法
(1)公式法: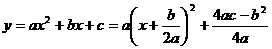 ,∴顶点是
,∴顶点是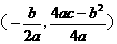 ,对称轴是直线
,对称轴是直线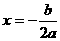 .
.
(2)配方法:运用配方的方法,将抛物线的解析式化为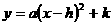 的形式,得到顶点为(
的形式,得到顶点为(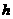 ,
,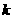 ),对称轴是直线
),对称轴是直线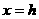 .
.
(3)运用抛物线的对称性:由于抛物线是以对称轴为轴的轴对称图形,所以对称轴的连线的垂直平分线是抛物线的对称轴,对称轴与抛物线的交点是顶点.用配方法求得的顶点,再用公式法或对称性进行验证,才能做到万无一失.
4.顶点决定抛物线的位置.几个不同的二次函数,如果二次项系数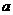 相同,那么抛物线的开口方向、开口大小完全相同,只是顶点的位置不同.
相同,那么抛物线的开口方向、开口大小完全相同,只是顶点的位置不同.
3.抛物线的三要素:开口方向、对称轴、顶点.
①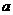 的符号决定抛物线的开口方向:当
的符号决定抛物线的开口方向:当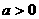 时,开口向上;当
时,开口向上;当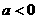 时,开口向下;
时,开口向下;
 相等,抛物线的开口大小、形状相同.
相等,抛物线的开口大小、形状相同.
②平行于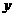 轴(或重合)的直线记作
轴(或重合)的直线记作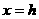 .特别地,
.特别地,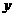 轴记作直线
轴记作直线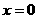 .
.
2.二次函数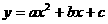 用配方法可化成:
用配方法可化成: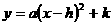 的形式,其中
的形式,其中 .
.
1.定义:一般地,如果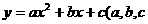 是常数,
是常数,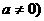 ,那么
,那么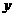 叫做
叫做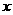 的二次函数.
的二次函数.
31、在△ABC中,AB=15,AC=13,BC边上高AD=12,试求△ABC周长。
30、 如图所示,在
如图所示,在 中,
中,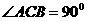 ,CD是AB边上高,若AD=8,BD=2,
,CD是AB边上高,若AD=8,BD=2,
求CD。
29、 如图所示,15只空油桶(每只油桶底面直径均为
如图所示,15只空油桶(每只油桶底面直径均为 )堆在一起,要给它盖一个遮雨棚,遮雨棚起码要多高?(结果保留一位小数)
)堆在一起,要给它盖一个遮雨棚,遮雨棚起码要多高?(结果保留一位小数)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com