
题目列表(包括答案和解析)
5.一蔬菜基地种植的某种绿色蔬菜,根据今年的市场行情,预测从五月一日起的50天内,它的市场售价y1与上市时间x的关系可用图(一)的一条线段表示;它的种植成本y2与上市时间x的关系可用图(二)中的抛物线的一部分来表示。
(1)求出图(一)中表示市场售价y1与上市时间x的函数关系式。
(2)求出图(二)中表示种植成本y2与上市时间x的函数关系式。
(3)假定市场售价减去种植成本为纯利润,问哪天上市的这种绿色蔬菜既不赔本
也不赚钱?(市场售价和种植成本的单位:元∕千克,时间单位:天)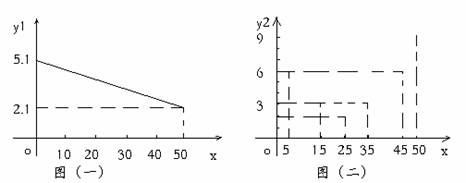
4.某市20名下岗职工在近郊承包50亩土地办农场。这些地可种蔬菜、烟叶或小麦,种这几种农作物每亩地所需职工数和产值预测如下表:
|
作物品种 |
每亩地所需职工数 |
每亩地预产值 |
|
蔬菜 |
1/2 |
1100元 |
|
烟叶 |
1/3 |
750元 |
|
小麦 |
1/4 |
600元 |
请你设计一种种植方案,使每亩地都种上农作物,20位职工都有工作,且使农作物预计总产量最多。
3.在双休日,某公司决定组织48名员工到附近一水上公园坐船游园,公司先派了一个人去了解船只的租金情况,这个人看到的租金价格表如下:
|
船 型 |
每只限载人数(人) |
租金(元) |
|
大船 |
5 |
3 |
|
小船 |
3 |
2 |
那么,怎样设计租船方案才能使所付租金最少?(严禁超载)
2.宜昌人引以为豪的夷陵广场坐落在城市中心的黄金宝地上,共占地5.5万平方米,是市政府拆迁商业城等建筑并投入1500万元建成的。
若在夷陵广场这片土地上修建商业写字楼,其建筑面积可以是土地面积的3倍,售出后每一平方米建筑面积市政府至少可以获得纯收入2400元。
问:如果将实际投入和可能获得的纯收入合并计算都看作投入,那么市政府为市民办实事修建夷陵广场至少投入了多少元?
是指把函数、方程(组)、不等式(组)与经济生活实例相结合的应用题。一般放在较新颖的背景下,以体现出时代特色,同时渗透思想教育,使学生在解题过程中获得情感体验。若试题能与当地实际社会生活结合,则尤为评价者称道。此类题目是目前中考热门题型,考生须重点研究。
这类题目一般文字较多,因此关键是读题。求解时应多读几遍题目,找清已知量,用字母表示出未知量,理清它们的关系,列出代数式、方程(组)、不等式(组)或函数表达式,即可求解。例如:
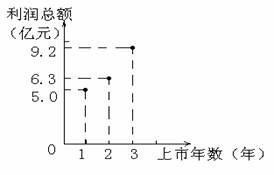
1.东风汽车股份有限公司是二汽1999年上市的一个子公司,上市后为迎接中国加入“WTO”的挑战,振兴中国汽车工业,公司员工及领导卧薪尝胆,艰苦奋战。三年来公司利润节节攀升,在中国加入世贸的2001年,公司也取得创记录的好成绩9.2亿元(如图)。
(1)写出图中三点确定的二次函数表达式;
(2)由于公司开展了“增收节支”活动,从而生产成本大大减少,在汽车售价微降的同时利润率仍以每年3个百分点的速率上升,若公司1999年利润率为15%,试问2001年公司销售收入达到多少元?
(3)公司欲超常规发展,定下目标在2002年的利润仍以图中抛物线的上升速率上升,已知公司1-3月平均每月销售收入为5亿元,照此推算,2002年公司是否会达到或超过目标?
7.从1开始,将连续的奇数相加,和的情况有如下规律:
此规律,1=1=12;1+3=4=22;1+3+5=9=32;1+3+5+7=16=42;1+3+5+7+9=25=52;…
按请你猜想从1开始,将前10个奇数(即当最后一个奇数是19时),它们的和是 。
6.我们平常用的数是十进制数,如2639=2×103+6×102+3×101+9×100,表示十进制的数要用10个数码(又叫数字):0,1,2,3,4,5,6,7,8,9。在电子数字计算机中用的是二进制,只要两个数码:0和1。如二进制中101=1×22+0×21+1×20等于十进制的数5,10111=1×24+0×23+1×22+1×21+1×20等于十进制中的数23,那么二进制中的1101等于十进制的数 。
5.小明是一位刻苦学习、勤于思考、勇于创造的同学。一天,他在解方程时,突然产生了这样的想法,x2=-1这个方程在实数范围内无解,如果存在一个数i2=-1,那么方程x2=-1可以变为x2=i2,则x=+i,从而x=+i是方程x2=-1的两个根。小明还发现i具有如下性质:
i1=i;i2=-1;i3=i2×i=(-1)×i=-i;i4=(i2)2=(-1)2=1;i5=i4×i=i;i6=(i2)3=(-1)3=-1;i7=i6×i=-i;i8=(i4)2=1……,请你观察上述各式,根据你发现的规律填空:i4n+1= ,i4n+2= ,i4n+3= (n为自然数)。
4.将正偶数按下表排成5列:
第1列 第2列 第3列 第4列 第5列
第1行 2 4 6 8
第2行 16 14 12 10
第3行 18 20 22 24
…… …… 28 26
根据上面排列规律,则2000应在( )
A.第125 行,第1 列; B.第125行,第2列;
C.第 250 行,第 1 列; D.第 250 行,第 2 列;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com