
题目列表(包括答案和解析)
4.(•河北省)在一平直河岸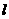 同侧有A、B两个村庄,A、B到
同侧有A、B两个村庄,A、B到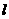 的距离分别是3km和2km,AB=a km
的距离分别是3km和2km,AB=a km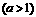 .现计划在河岸
.现计划在河岸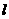 上建一抽水站P,用输水管向两个村庄供水.
上建一抽水站P,用输水管向两个村庄供水.
方案设计
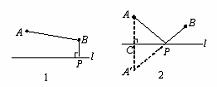
某班数学兴趣小组设计了两种铺设管道方案:图1是方案一的示意图,设该方案中管道长度为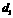 ,且
,且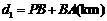 (其中
(其中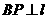 于点P);图2是方案二的示意图,设该方案中管道长度为
于点P);图2是方案二的示意图,设该方案中管道长度为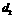 ,且
,且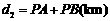 (其中点
(其中点 与点A关于
与点A关于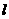 对称,
对称,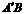 与
与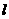 交于点P).
交于点P).
观察计算
(1)在方案一中,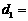 km(用含a的式子表示);
km(用含a的式子表示);
(2)在方案二中,组长小宇为了计算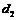 的长,作了如图3所示的辅助线,请你按小宇同学的思路计算,
的长,作了如图3所示的辅助线,请你按小宇同学的思路计算,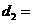
km(用含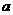 的式子表示).
的式子表示).
探索归纳
(1)①当a=4时,比较大小: (填“>”、“=”或“<”);
(填“>”、“=”或“<”);
②当a=6时,比较大小: (填“>”、“=”或“<”);
(填“>”、“=”或“<”);
(2)请你参考边方框中的方法指导,

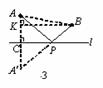
就a(当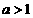 时)的所有取值情况进行分析,要使铺设的管道长度较短,
时)的所有取值情况进行分析,要使铺设的管道长度较短,
应选择方案一还是方案二?
第5课时 方案设计题 答案
3.(·咸宁市)“5·12”四川汶川大地震的灾情牵动全国人民的心,某市A、B两个蔬菜基地得知四川C、D两个灾民安置点分别急需蔬菜240吨和260吨的消息后,决定调运蔬菜支援灾区.已知A蔬菜基地有蔬菜200吨,B蔬菜基地有蔬菜300吨,现将这些蔬菜全部调往C、D两个灾民安置点.从A地运往C、D两处的费用分别为每吨20元和25元,从B地运往C、D两处的费用分别为每吨15元和18元.设从B地运往C处的蔬菜为x吨.
(1)请填写下表,并求两个蔬菜基地调运蔬菜的运费相等时x的值;
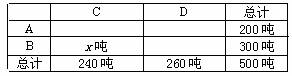

(2)设A、B两个蔬菜基地的总运费为w元,写出w与x之间的函数关系式,并求总运费最小的调运方案;
(3)经过抢修,从B地到C处的路况得到进一步改善,缩短了运输时间,运费每吨减少 元(
元( >0),其余线路的运费不变,试讨论总运费最小的调运方案.
>0),其余线路的运费不变,试讨论总运费最小的调运方案.





类型之三 测量方案问题
《新课程标准》要求同学们学会运用数学知识解决日常生活和其他学科中的问题.测量方案问题正是这样的问题,在解决这样的问题时要注意方案的可行性.
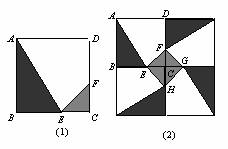
2.(•荆门市)某人定制了一批地砖,每块地砖(如图(1)所示)是边长为0.4米的正方形ABCD,点E、F分别在边BC和CD上,△CFE、△ABE和四边形AEFD均由单一材料制成,制成△CFE、△ABE和四边形AEFD的三种材料的每平方米价格依次为30元、20元、10元,若将此种地砖按图(2)所示的形式铺设,且能使中间的阴影部分组成四边形EFGH.
(1)判断图(2)中四边形EFGH是何形状,并说明理由;
(2)E、F在什么位置时,定制这批地砖所需的材料费用最省?







类型之二 经济类方案设计题
在日常生产和生活中每时每刻都要用到决策,方案决策题已成为中考热点题型之一,
这些问题可以结合方程和不等式(组)来解决.关键是要抓住题中问题的实际意义,将其转化为数学问题.
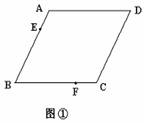
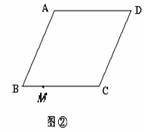
1.(•莆田市)某市要在一块平行四边形ABCD的空地上建造一个四边形花园,要求花园所占面积是 ABCD面积的一半,并且四边形花园的四个顶点作为出人口,要求分别在
ABCD面积的一半,并且四边形花园的四个顶点作为出人口,要求分别在 ABCD的四条边上,请你设计两种方案:
ABCD的四条边上,请你设计两种方案:
方案(1):如图(1)所示,两个出入口E、F已确定,请在图(1)上画出符合要求的四边形花园,并简要说明画法;
方案(2):如图(2)所示,一个出入口M已确定,请在图(2)上画出符合要求的梯形花园,并简要说明画法. 




10.[解析]从表格中的数据我们可以看出当x增加10时,对应y的值减小100,所以y与x之间可能是一次函数的关系,我们可以根据图象发现这些点在一条直线上,所以y与x之间是一次函数的关系,然后设出一次函数关系式,求出其关系式.
[答案](1)画图如图;
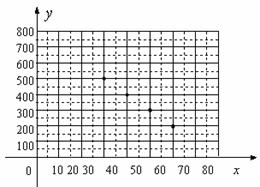
由图可猜想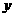 与
与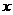 是一次函数关系,
是一次函数关系,
设这个一次函数为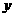 =
= 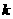
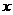 +
+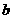 (k≠0)
(k≠0)
∵这个一次函数的图象经过(30,500)、(40,400)这两点,
∴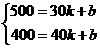 解得
解得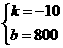
∴函数关系式是: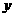 =-10
=-10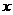 +800
+800
(2)设工艺厂试销该工艺品每天获得的利润是W元,依题意得
W=(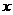 -20)(-10
-20)(-10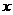 +800)=-10
+800)=-10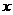
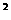 +1000
+1000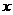 -16000
-16000
=-10(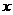 -50)
-50)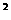 +9000
+9000
∴当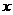 =50时,W有最大值9000.
=50时,W有最大值9000.
所以,当销售单价定为50元∕件时,工艺厂试销该工艺品每天获得的利润最大,最大利润是9000元.
(3)对于函数 W=-10(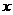 -50)
-50)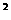 +9000,
+9000,
当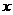 ≤45时,W的值随着x值的增大而增大,销售单价定为45元∕件时,工艺厂试销该工艺品每天获得的利润最大.
≤45时,W的值随着x值的增大而增大,销售单价定为45元∕件时,工艺厂试销该工艺品每天获得的利润最大.
9.[解析]观察分数的排列发现其分布有轴对称性,且(n,1)表示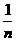 ,(n,2)表示
,(n,2)表示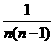
[答案]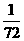
8.[解析]寻求图形与图形之间数字蕴含的规律是解题的关键所在.图形的第一行的数是连续正奇数;第二行左边的数是连续正偶数;把每个图形第一行的数乘以第二行左边的数,再加上第一行的数,便得到第二行右边的数.
[答案]
7.[解析]此题为统计与概率知识的综合题,由条形统计图可以判断出三种比赛项目的具体人数,就可以解决第一、二两问.第三问乒乓球门票的价格需要根据统计表中所示的各门票的价格与购买乒乓球门票的总款数占全部门票总款数的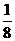 ,构造方程从而求出乒乓球门票的价格.
,构造方程从而求出乒乓球门票的价格.
[答案](12分)(1)30,20
(3)解法一:依题意,有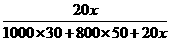 = .
= .
解得x =500 .
经检验,x =500是原方程的解.
答:每张乒乓球门票的价格为500元.
解法二:依题意,有 =
= 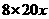 .
.
解得x =500 .
答:每张乒乓球门票的价格为500元.
6.[解析]由图可知点P运动路程在4和9之间时三角形ABP面积不变,说明这时点P在CD边上,因此可知CD=5,BC=4,三角形ABC面积为10
[答案]A
5.[解析]由图象可以知道快艇用时4个小时路程160千米,速度每小时40千米,同样可以得到轮船速度每小时20千米,快艇比轮船晚出发2小时,早到2小时,中间在4小时的时候追上轮船.
[答案]D
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com