
题目列表(包括答案和解析)
1.
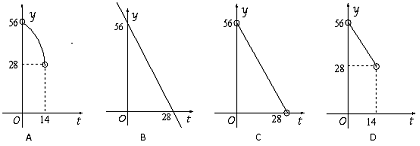 如图,在直角梯形ABCD中,DC∥AB,∠A=90°,AB=28cm,DC=24cm,AD=4cm,点M从点D出发,以1cm/s的速度向点C运动,点N从点B同时出发,以2cm/s的速度向点A运动,当其中一个动点到达端点停止运动时,另一个动点也随之停止运动.则四边形AMND的面积y(cm2)与两动点运动的时间t(s)的函数图象大致是(
)
如图,在直角梯形ABCD中,DC∥AB,∠A=90°,AB=28cm,DC=24cm,AD=4cm,点M从点D出发,以1cm/s的速度向点C运动,点N从点B同时出发,以2cm/s的速度向点A运动,当其中一个动点到达端点停止运动时,另一个动点也随之停止运动.则四边形AMND的面积y(cm2)与两动点运动的时间t(s)的函数图象大致是(
)
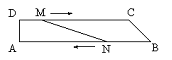
4、如图,梯形OABC中,O为直角坐标系的原点,A、B、C的坐标分别为(14,0)、(14,3)、(4,3)。点P、Q同时从原点出发,分别作匀速运动。其中点P沿OA向终点A运动,速度为每秒1个单位;点Q沿OC、CB向终点B运动。当这两点中有一点到达自己的终点时,另一点也停止运动.
(1)设从出发起运动了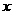 秒,如果点Q的速度为每秒2个单位,试分别写出这时点Q在OC上或在CB上时的坐标(用含
秒,如果点Q的速度为每秒2个单位,试分别写出这时点Q在OC上或在CB上时的坐标(用含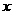 的代数式表示,不要求写出
的代数式表示,不要求写出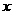 的取值范围);
的取值范围);
(2)设从出发起运动了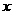 秒,如果点P与点Q所经过的路程之和恰好为梯形OABC的周长的一半.
秒,如果点P与点Q所经过的路程之和恰好为梯形OABC的周长的一半.
①试用含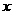 的代数式表示这时点Q所经过的路程和它的速度;
的代数式表示这时点Q所经过的路程和它的速度;
②试问:这时直线PQ是否可能同时把梯形OABC的面积也分成相等的两部分?如有可能,求出相应5的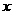 的值和P、Q的坐标;如不可能,请说明理由.
的值和P、Q的坐标;如不可能,请说明理由.
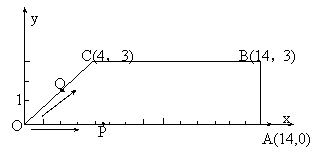 分析:本例是平面直角坐标系与方程、函数、不等式及几何型问题的综合题,解题关键是正确地用
分析:本例是平面直角坐标系与方程、函数、不等式及几何型问题的综合题,解题关键是正确地用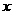 的代数式表示出点的坐标,特别注意直线PQ同时把梯形OABC的面积也分成相等的两部分要分两类讨论.
的代数式表示出点的坐标,特别注意直线PQ同时把梯形OABC的面积也分成相等的两部分要分两类讨论.
作业:
3、如图,在矩形ABCD中,AB=6米,BC=8米,动点P以2米/秒的速度从点A出发,沿AC向点C移动,同时动点Q以1米/秒的速度从点C出发,沿CB向点B移动,设P、Q两点移动t秒(0<t<5)后,四边形ABQP的面积为S米2。(1)求面积S与时间t的关系式;
(2)在P、Q两点移动的过程中,四边形ABQP与△CPQ的面积能否相等?若能,求出此时点P的位置;若不能,请说明理由。
分析:本题是一个动态几何问题,也是一个数形结合的典型问题,综合性较强。
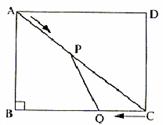
2、如图,在平行四边形ABCD中,AD=4 cm,∠A=60°,BD⊥AD. 一动点P从A出发,以每秒1 cm的速度沿A→B→C的路线匀速运动,过点P作直线PM,使PM⊥AD .
(1) 当点P运动2秒时,设直线PM与AD相交于点E,求△APE的面积;
(2) 当点P运动2秒时,另一动点Q也从A出发沿A→B→C的路线运动,且在AB上以每秒1 cm的速度匀速运动,在BC上以每秒2 cm的速度匀速运动. 过Q作直线QN,使QN∥PM. 设点Q运动的时间为t秒(0≤t≤10),直线PM与QN截平行四边形ABCD所得图形的面积为S cm2 .
 ① 求S关于t的函数关系式;
① 求S关于t的函数关系式;
② (附加题) 求S的最大值.
1、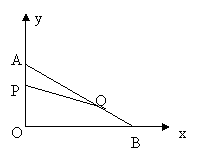 如图,在平面直角坐标系内,已知点A(0,6)、点B(8,0),动点P从点A开始在线段AO上以每秒1个单位长度的速度向点O移动,同时动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A移动,设点P、Q移动的时间为t秒.(1) 求直线AB的解析式;(2) 当t为何值时,△APQ与△AOB相似? (3) 当t为何值时,△APQ的面积为
如图,在平面直角坐标系内,已知点A(0,6)、点B(8,0),动点P从点A开始在线段AO上以每秒1个单位长度的速度向点O移动,同时动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A移动,设点P、Q移动的时间为t秒.(1) 求直线AB的解析式;(2) 当t为何值时,△APQ与△AOB相似? (3) 当t为何值时,△APQ的面积为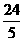 个平方单位?
个平方单位?
3、
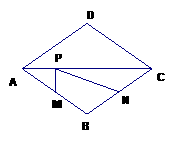
 如图,平行四边形ABCD中,对角线AC、BD相交于点O,若E、F是线段AC上的两个动点,分别从A、C两点以相同的速度1㎝/s向C、A运动,若BD=12㎝,AC=16㎝,当t
时,四边形DEBF为平行四边形;当时间t=
时,四边形DEBF为矩形。
如图,平行四边形ABCD中,对角线AC、BD相交于点O,若E、F是线段AC上的两个动点,分别从A、C两点以相同的速度1㎝/s向C、A运动,若BD=12㎝,AC=16㎝,当t
时,四边形DEBF为平行四边形;当时间t=
时,四边形DEBF为矩形。
例题讲解:
2、若点P为边长为5的等边三角形内的一个动点,作PD⊥BC于点D,PE⊥AC于点E,PF⊥AB于点F,则PD+PE+PF= ;反之,若PD=6,PE=10,PF=8,则等边△ABC的面积为 ;
1、如图,点P是边为1的菱形ABCD对角线AC的一个动点,点M、N分别是AB、BC的中点,则MP+NP的最小值是 ;
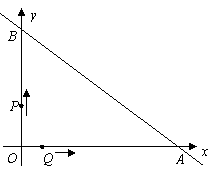
2、(09齐齐哈尔)直线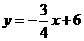 与坐标轴分别交于
与坐标轴分别交于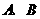 两点,动点
两点,动点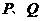 同时从
同时从 点出发,同时到达
点出发,同时到达 点,运动停止.点
点,运动停止.点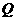 沿线段
沿线段 运动,速度为每秒1个单位长度,点
运动,速度为每秒1个单位长度,点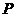 沿路线
沿路线 →
→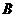 →
→ 运动.
运动.
(1)直接写出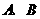 两点的坐标;
两点的坐标;
(2)设点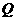 的运动时间为
的运动时间为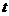 秒,
秒,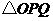 的面积为
的面积为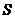 ,求出
,求出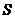 与
与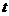 之间的函数关系式;
之间的函数关系式;
 (3)当
(3)当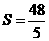 时,求出点
时,求出点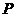 的坐标,并直接写出以点
的坐标,并直接写出以点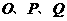 为顶点的平行四边形的第四个顶点
为顶点的平行四边形的第四个顶点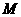 的坐标.
的坐标.
解(1)A(8,0)B(0,6)·················· 1分
(2)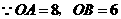
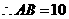
 点
点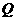 由
由 到
到 的时间是
的时间是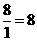 (秒)
(秒)
 点
点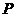 的速度是
的速度是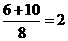 (单位/秒)·· 1分
(单位/秒)·· 1分
当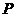 在线段
在线段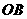 上运动(或0
上运动(或0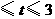 )时,
)时,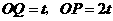
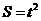 ··························································································································· 1分
··························································································································· 1分
当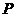 在线段
在线段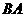 上运动(或
上运动(或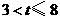 )时,
)时,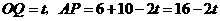 ,
,
如图,作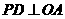 于点
于点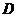 ,由
,由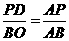 ,得
,得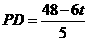 ,··································· 1分
,··································· 1分
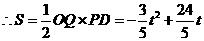 ·················································································· 1分
·················································································· 1分
(自变量取值范围写对给1分,否则不给分.)
(3)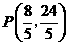 ··········································································································· 1分
··········································································································· 1分
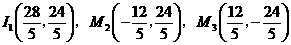 ···························································· 3分
···························································· 3分
3(09深圳)如图,在平面直角坐标系中,直线l:y=-2x-8分别与x轴,y轴相交于A,B两点,点P(0,k)是y轴的负半轴上的一个动点,以P为圆心,3为半径作⊙P.
(1)连结PA,若PA=PB,试判断⊙P与x轴的位置关系,并说明理由;
(2)当k为何值时,以⊙P与直线l的两个交点和圆心P为顶点的三角形是正三角形?
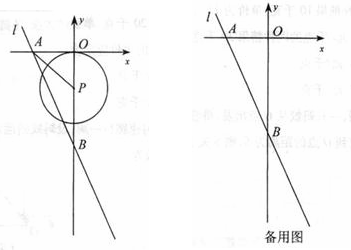
解:(1)⊙P与x轴相切.
∵直线y=-2x-8与x轴交于A(4,0),
与y轴交于B(0,-8),
∴OA=4,OB=8.
由题意,OP=-k,
∴PB=PA=8+k.
在Rt△AOP中,k2+42=(8+k)2,
∴k=-3,∴OP等于⊙P的半径,
∴⊙P与x轴相切.
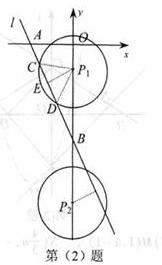 (2)设⊙P与直线l交于C,D两点,连结PC,PD当圆心P在线段OB上时,作PE⊥CD于E.
(2)设⊙P与直线l交于C,D两点,连结PC,PD当圆心P在线段OB上时,作PE⊥CD于E.
∵△PCD为正三角形,∴DE=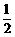 CD=
CD=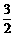 ,PD=3,
,PD=3,
∴PE=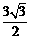 .
.
∵∠AOB=∠PEB=90°, ∠ABO=∠PBE,
∴△AOB∽△PEB,
∴
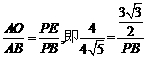 ,
,
∴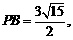
∴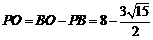 ,
,
∴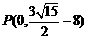 ,
,
∴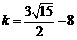 .
.
当圆心P在线段OB延长线上时,同理可得P(0,-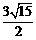 -8),
-8),
∴k=-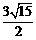 -8,
-8,
∴当k=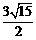 -8或k=-
-8或k=-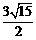 -8时,以⊙P与直线l的两个交点和圆心P为顶点的三角形是正三角形.
-8时,以⊙P与直线l的两个交点和圆心P为顶点的三角形是正三角形.
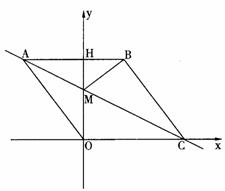
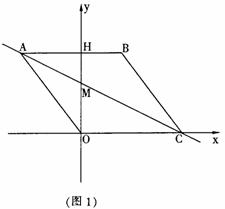
4(09哈尔滨) 如图1,在平面直角坐标系中,点O是坐标原点,四边形ABCO是菱形,点A的坐标为(-3,4),
点C在x轴的正半轴上,直线AC交y轴于点M,AB边交y轴于点H.
(1)求直线AC的解析式;
(2)连接BM,如图2,动点P从点A出发,沿折线ABC方向以2个单位/秒的速度向终点C匀速运动,设△PMB的面积为S(S≠0),点P的运动时间为t秒,求S与t之间的函数关系式(要求写出自变量t的取值范围);
(3)在(2)的条件下,当 t为何值时,∠MPB与∠BCO互为余角,并求此时直线OP与直线AC所夹锐角的正切值.
解:
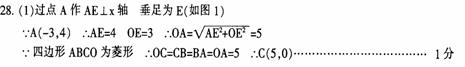

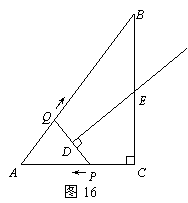 5(09河北)在Rt△ABC中,∠C=90°,AC = 3,AB = 5.点P从点C出发沿CA以每秒1个单位长的速度向点A匀速运动,到达点A后立刻以原来的速度沿AC返回;点Q从点A出发沿AB以每秒1个单位长的速度向点B匀速运动.伴随着P、Q的运动,DE保持垂直平分PQ,且交PQ于点D,交折线QB-BC-CP于点E.点P、Q同时出发,当点Q到达点B时停止运动,点P也随之停止.设点P、Q运动的时间是t秒(t>0).
5(09河北)在Rt△ABC中,∠C=90°,AC = 3,AB = 5.点P从点C出发沿CA以每秒1个单位长的速度向点A匀速运动,到达点A后立刻以原来的速度沿AC返回;点Q从点A出发沿AB以每秒1个单位长的速度向点B匀速运动.伴随着P、Q的运动,DE保持垂直平分PQ,且交PQ于点D,交折线QB-BC-CP于点E.点P、Q同时出发,当点Q到达点B时停止运动,点P也随之停止.设点P、Q运动的时间是t秒(t>0).
(1)当t = 2时,AP = ,点Q到AC的距离是 ;
(2)在点P从C向A运动的过程中,求△APQ的面积S与
t的函数关系式;(不必写出t的取值范围)
(3)在点E从B向C运动的过程中,四边形QBED能否成
为直角梯形?若能,求t的值.若不能,请说明理由;
(4)当DE经过点C 时,请直接写出t的值.
解:(1)1,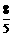 ;
;
(2)作QF⊥AC于点F,如图3, AQ = CP= t,∴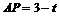 .
.
由△AQF∽△ABC,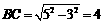 ,
,
得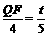 .∴
.∴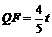 .
.
 ∴
∴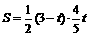 ,
,
即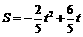 .
.
(3)能.
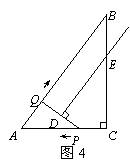
①当DE∥QB时,如图4.
∵DE⊥PQ,∴PQ⊥QB,四边形QBED是直角梯形.
此时∠AQP=90°.
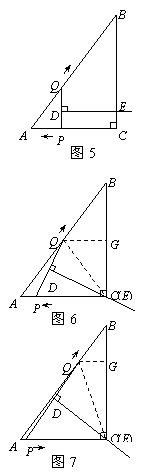 由△APQ ∽△ABC,得
由△APQ ∽△ABC,得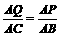 ,
,
即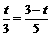 . 解得
. 解得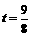 .
.
②如图5,当PQ∥BC时,DE⊥BC,四边形QBED是直角梯形.
此时∠APQ =90°.
由△AQP ∽△ABC,得 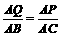 ,
,
即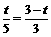 . 解得
. 解得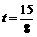 .
.
(4)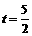 或
或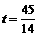 .
.
①点P由C向A运动,DE经过点C.
连接QC,作QG⊥BC于点G,如图6.
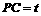 ,
,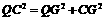
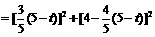 .
.
由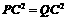 ,得
,得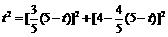 ,解得
,解得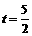 .
.
②点P由A向C运动,DE经过点C,如图7.
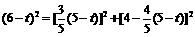 ,
,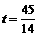 ]
]
6(09河南))如图,在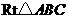 中,
中,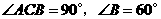 ,
,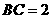 .点
.点 是
是 的中点,过点
的中点,过点 的直线
的直线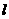 从与
从与 重合的位置开始,绕点
重合的位置开始,绕点 作逆时针旋转,交
作逆时针旋转,交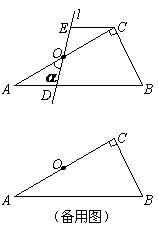
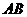 边于点
边于点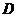 .过点
.过点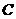 作
作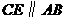 交直线
交直线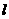 于点
于点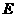 ,设直线
,设直线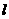 的旋转角为
的旋转角为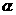 .
.


(1)①当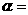 度时,四边形
度时,四边形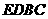 是等腰梯形,此时
是等腰梯形,此时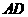 的长为 ;
的长为 ;


②当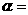 度时,四边形
度时,四边形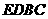 是直角梯形,此时
是直角梯形,此时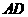 的长为 ;
的长为 ;
(2)当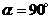 时,判断四边形
时,判断四边形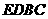 是否为菱形,并说明理由.
是否为菱形,并说明理由.
解(1)①30,1;②60,1.5; ……………………4分
(2)当∠α=900时,四边形EDBC是菱形.
∵∠α=∠ACB=900,∴BC//ED.
∵CE//AB, ∴四边形EDBC是平行四边形. ……………………6分
在Rt△ABC中,∠ACB=900,∠B=600,BC=2,
∴∠A=300.
∴AB=4,AC=2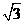 .
.
∴AO=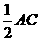 =
=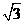 .
……………………8分
.
……………………8分
在Rt△AOD中,∠A=300,∴AD=2.
∴BD=2.
∴BD=BC.
又∵四边形EDBC是平行四边形,
∴四边形EDBC是菱形 ……………………10分
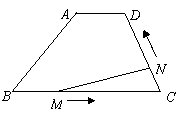 7(09济南)如图,在梯形
7(09济南)如图,在梯形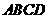 中,
中,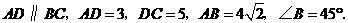 动点
动点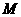 从
从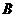 点出发沿线段
点出发沿线段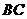 以每秒2个单位长度的速度向终点
以每秒2个单位长度的速度向终点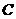 运动;动点
运动;动点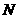 同时从
同时从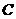 点出发沿线段
点出发沿线段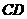 以每秒1个单位长度的速度向终点
以每秒1个单位长度的速度向终点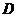 运动.设运动的时间为
运动.设运动的时间为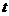 秒.
秒.
(1)求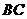 的长.
的长.
(2)当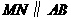 时,求
时,求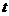 的值.
的值.
(3)试探究: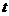 为何值时,
为何值时,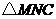 为等腰三角形.
为等腰三角形.
解:(1)如图①,过 、
、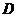 分别作
分别作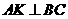 于
于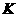 ,
,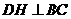 于
于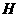 ,则四边形
,则四边形 是矩形
是矩形
∴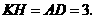 ····························································································· 1分
····························································································· 1分
在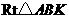 中,
中,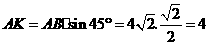
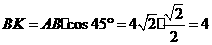 ···································································· 2分
···································································· 2分
在 中,由勾股定理得,
中,由勾股定理得,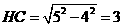
∴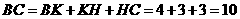 ························································· 3分
························································· 3分
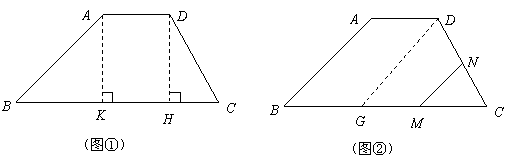
(2)如图②,过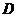 作
作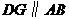 交
交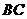 于
于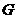 点,则四边形
点,则四边形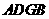 是平行四边形
是平行四边形
∵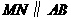
∴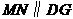
∴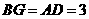
∴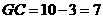 ·························································································· 4分
·························································································· 4分
由题意知,当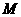 、
、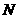 运动到
运动到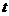 秒时,
秒时,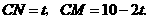
∵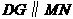
∴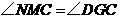
又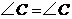
∴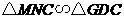
∴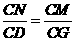 ································································································· 5分
································································································· 5分
即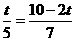
解得,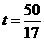 ·································································································· 6分
·································································································· 6分
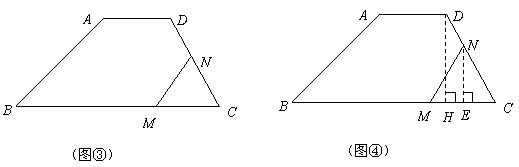
(3)分三种情况讨论:
①当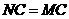 时,如图③,即
时,如图③,即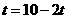
∴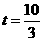 ········································································································· 7分
········································································································· 7分
②当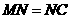 时,如图④,过
时,如图④,过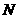 作
作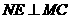 于
于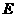
解法一:
由等腰三角形三线合一性质得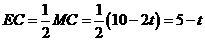
在 中,
中,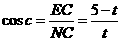
又在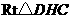 中,
中,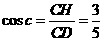
∴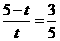
解得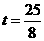 ····································································································· 8分
····································································································· 8分
解法二:
∵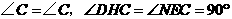
∴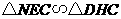
∴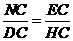
即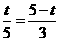
∴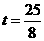 ········································································································· 8分
········································································································· 8分
③当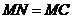 时,如图⑤,过
时,如图⑤,过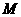 作
作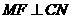 于
于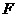 点.
点.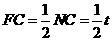
解法一:(方法同②中解法一)
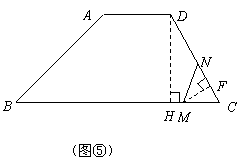
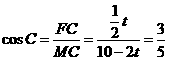
解得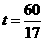
解法二:
∵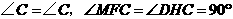
∴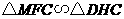
∴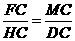
即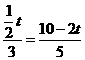
∴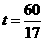
综上所述,当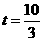 、
、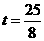 或
或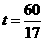 时,
时,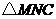 为等腰三角形·················· 9分
为等腰三角形·················· 9分
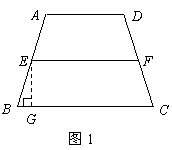
8(09江西)如图1,在等腰梯形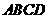 中,
中,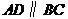 ,
,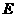 是
是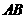 的中点,过点
的中点,过点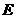 作
作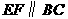 交
交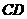 于点
于点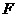 .
.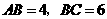 ,
,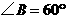 .
.
(1)求点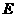 到
到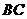 的距离;
的距离;
(2)点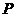 为线段
为线段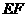 上的一个动点,过
上的一个动点,过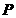 作
作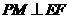 交
交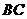 于点
于点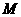 ,过
,过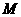 作
作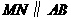 交折线
交折线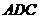 于点
于点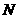 ,连结
,连结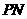 ,设
,设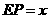 .
.
①当点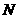 在线段
在线段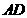 上时(如图2),
上时(如图2),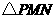 的形状是否发生改变?若不变,求出
的形状是否发生改变?若不变,求出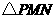 的周长;若改变,请说明理由;
的周长;若改变,请说明理由;
②当点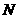 在线段
在线段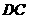 上时(如图3),是否存在点
上时(如图3),是否存在点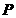 ,使
,使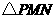 为等腰三角形?若存在,请求出所有满足要求的
为等腰三角形?若存在,请求出所有满足要求的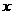 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
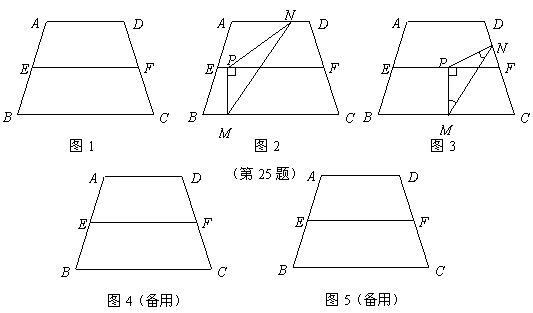
解(1)如图1,过点 作
作 于点
于点 ························· 1分
························· 1分
 ∵
∵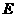 为
为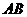 的中点,
的中点,
∴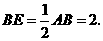
在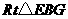 中,
中,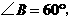 ∴
∴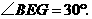 ············· 2分
············· 2分
∴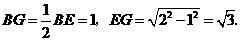
即点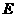 到
到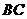 的距离为
的距离为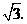 ··········································· 3分
··········································· 3分
(2)①当点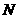 在线段
在线段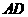 上运动时,
上运动时,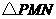 的形状不发生改变.
的形状不发生改变.
∵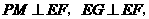 ∴
∴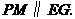
∵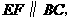 ∴
∴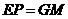 ,
,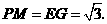
同理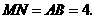 ······························································································· 4分
······························································································· 4分
如图2,过点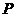 作
作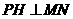 于
于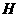 ,∵
,∵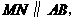
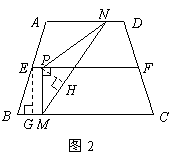 ∴
∴
∴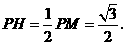
∴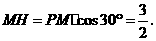
则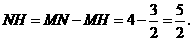
在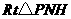 中,
中,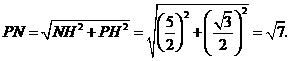
∴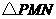 的周长=
的周长=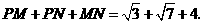 ············································· 6分
············································· 6分
②当点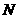 在线段
在线段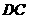 上运动时,
上运动时,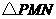 的形状发生改变,但
的形状发生改变,但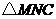 恒为等边三角形.
恒为等边三角形.
当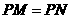 时,如图3,作
时,如图3,作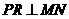 于
于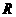 ,则
,则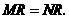
类似①,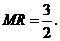
∴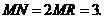 ································································································ 7分
································································································ 7分
∵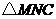 是等边三角形,∴
是等边三角形,∴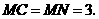
此时,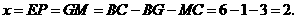 ········································· 8分
········································· 8分
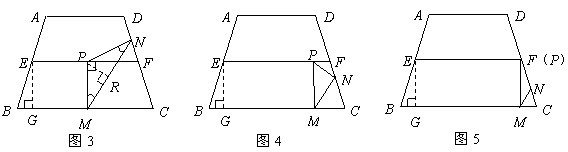
 当
当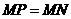 时,如图4,这时
时,如图4,这时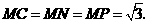
此时,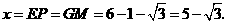
当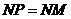 时,如图5,
时,如图5,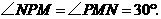
则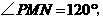 又
又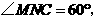
∴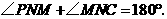
因此点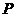 与
与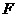 重合,
重合,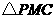 为直角三角形.
为直角三角形.
∴
此时,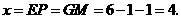
综上所述,当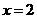 或4或
或4或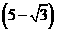 时,
时, 为等腰三角形.························ 10分
为等腰三角形.························ 10分
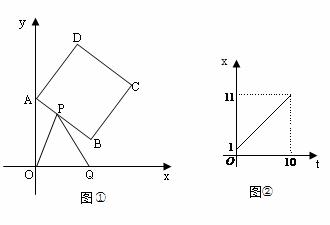
9(09兰州)如图①,正方形 ABCD中,点A、B的坐标分别为(0,10),(8,4),
点C在第一象限.动点P在正方形 ABCD的边上,从点A出发沿A→B→C→D匀速运动,
同时动点Q以相同速度在x轴正半轴上运动,当P点到达D点时,两点同时停止运动,
设运动的时间为t秒.
(1)当P点在边AB上运动时,点Q的横坐标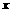 (长度单位)关于运动时间t(秒)的函数图象如图②所示,请写出点Q开始运动时的坐标及点P运动速度;
(长度单位)关于运动时间t(秒)的函数图象如图②所示,请写出点Q开始运动时的坐标及点P运动速度;
(2)求正方形边长及顶点C的坐标;
(3)在(1)中当t为何值时,△OPQ的面积最大,并求此时P点的坐标;
(4)如果点P、Q保持原速度不变,当点P沿A→B→C→D匀速运动时,OP与PQ能否相等,若能,写出所有符合条件的t的值;若不能,请说明理由.
解:(1)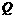 (1,0)···································································································· 1分
(1,0)···································································································· 1分
点P运动速度每秒钟1个单位长度.··········································································· 2分
(2) 过点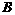 作BF⊥y轴于点
作BF⊥y轴于点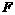 ,
,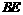 ⊥
⊥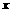 轴于点
轴于点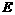 ,则
,则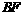 =8,
=8,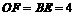 .
.
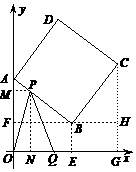 ∴
∴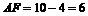 .
.
在Rt△AFB中,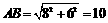 3分
3分
过点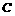 作
作 ⊥
⊥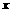 轴于点
轴于点 ,与
,与 的延长线交于点
的延长线交于点 .
.
∵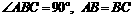 ∴△ABF≌△BCH.
∴△ABF≌△BCH.
∴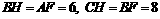 .
.
∴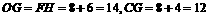 .
.
∴所求C点的坐标为(14,12). 4分
(3) 过点P作PM⊥y轴于点M,PN⊥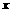 轴于点N,
轴于点N,
则△APM∽△ABF.
∴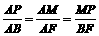 .
.
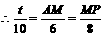 .
.
∴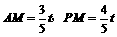 .
∴
.
∴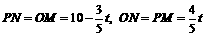 .
.
设△OPQ的面积为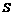 (平方单位)
(平方单位)
∴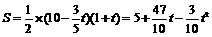 (0≤
(0≤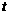 ≤10) ························································ 5分
≤10) ························································ 5分
说明:未注明自变量的取值范围不扣分.
∵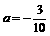 <0 ∴当
<0 ∴当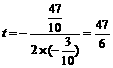 时, △OPQ的面积最大.······························ 6分
时, △OPQ的面积最大.······························ 6分
此时P的坐标为(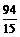 ,
,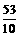 ) .················································································· 7分
) .················································································· 7分
(4) 当 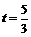 或
或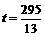 时,
OP与PQ相等.························································· 9分
时,
OP与PQ相等.························································· 9分
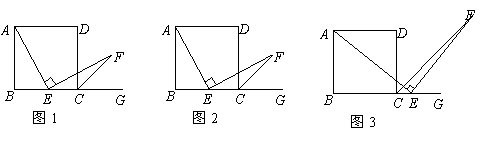
10(09临沂)数学课上,张老师出示了问题:如图1,四边形ABCD是正方形,点E是边BC的中点.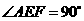 ,且EF交正方形外角
,且EF交正方形外角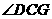 的平行线CF于点F,求证:AE=EF.
的平行线CF于点F,求证:AE=EF.
经过思考,小明展示了一种正确的解题思路:取AB的中点M,连接ME,则AM=EC,易证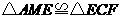 ,所以
,所以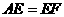 .
.
在此基础上,同学们作了进一步的研究:
(1)小颖提出:如图2,如果把“点E是边BC的中点”改为“点E是边BC上(除B,C外)的任意一点”,其它条件不变,那么结论“AE=EF”仍然成立,你认为小颖的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由;
(2)小华提出:如图3,点E是BC的延长线上(除C点外)的任意一点,其他条件不变,结论“AE=EF”仍然成立.你认为小华的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由.
解:(1)正确.··························································· (1分)
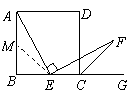 证明:在
证明:在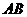 上取一点
上取一点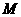 ,使
,使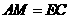 ,连接
,连接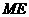 . (2分)
. (2分)
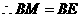 .
.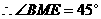 ,
,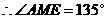 .
.
 是外角平分线,
是外角平分线,
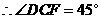 ,
,
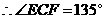 .
.
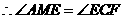 .
.
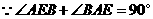 ,
,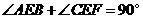 ,
,

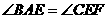 .
.
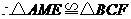 (ASA).············································································ (5分)
(ASA).············································································ (5分)
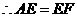 .······································································································· (6分)
.······································································································· (6分)
(2)正确.····························································· (7分)
证明:在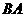 的延长线上取一点
的延长线上取一点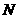 .
.
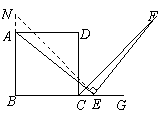 使
使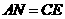 ,连接
,连接 .········································ (8分)
.········································ (8分)
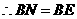 .
.
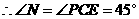 .
.
 四边形
四边形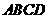 是正方形,
是正方形,
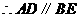 .
.
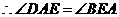 .
.
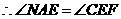 .
.
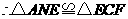 (ASA).··········································································· (10分)
(ASA).··········································································· (10分)
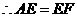 .······································································································ (11分)
.······································································································ (11分)
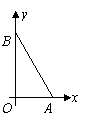
11(09天津)已知一个直角三角形纸片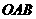 ,其中
,其中 .如图,将该纸片放置在平面直角坐标系中,折叠该纸片,折痕与边
.如图,将该纸片放置在平面直角坐标系中,折叠该纸片,折痕与边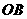 交于点
交于点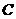 ,与边
,与边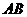 交于点
交于点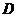 .
.
 (Ⅰ)若折叠后使点
(Ⅰ)若折叠后使点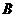 与点
与点 重合,求点
重合,求点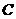 的坐标;
的坐标;
试题详情
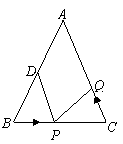
1、(09包头)如图,已知 中,
中, 厘米,
厘米,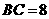 厘米,点
厘米,点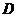 为
为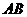 的中点.
的中点.
(1)如果点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.
 ①若点Q的运动速度与点P的运动速度相等,经过1秒后,
①若点Q的运动速度与点P的运动速度相等,经过1秒后,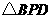 与
与 是否全等,请说明理由;
是否全等,请说明理由;
②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使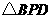 与
与 全等?
全等?
(2)若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿 三边运动,求经过多长时间点P与点Q第一次在
三边运动,求经过多长时间点P与点Q第一次在 的哪条边上相遇?
的哪条边上相遇?
解:(1)①∵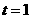 秒,
秒,
∴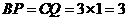 厘米,
厘米,
∵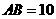 厘米,点
厘米,点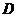 为
为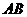 的中点,
的中点,
∴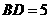 厘米.
厘米.
又∵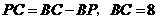 厘米,
厘米,
∴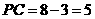 厘米,
厘米,
∴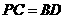 .
.
又∵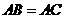 ,
,
∴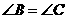 ,
,
∴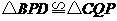 .·························································································· (4分)
.·························································································· (4分)
②∵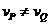 , ∴
, ∴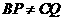 ,
,
又∵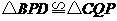 ,
,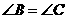 ,则
,则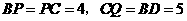 ,
,
∴点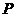 ,点
,点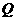 运动的时间
运动的时间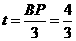 秒,
秒,
∴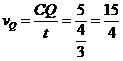 厘米/秒.············································································· (7分)
厘米/秒.············································································· (7分)
(2)设经过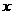 秒后点
秒后点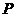 与点
与点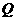 第一次相遇,
第一次相遇,
由题意,得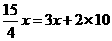 ,
,
解得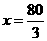 秒.
秒.
∴点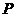 共运动了
共运动了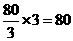 厘米.
厘米.
∵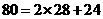 ,
,
∴点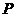 、点
、点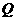 在
在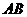 边上相遇,
边上相遇,
∴经过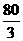 秒点
秒点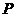 与点
与点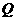 第一次在边
第一次在边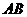 上相遇.················································ (12分)
上相遇.················································ (12分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com