
题目列表(包括答案和解析)
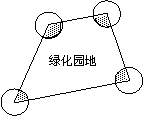
7.如图,一块四边形绿化园地,四角都做有半径为R的圆形喷水池,则这四个喷水池占去的绿化园地的面积为( )
A、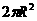 B、
B、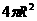 C、
C、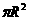 D、不能确定
D、不能确定
6.如图,在长为a的正方形中挖掉一个边长为b的小正方形(a>b)把余下的部分剪拼成一个矩形,通过计算两个图形(阴影部分)的面积,验证了一个等式,则这个等式是( )
A.a2-b2=(a+b)(a-b) B.(a+b)2=a2+2ab+b2
C.(a-b)2=a2-2ab+b2 D.(a+2b)(a-b)=a2+ab-2b2
5.若x2+mx+1是完全平方式,则m=( )。
A.2 B.-2 C.±2 D.±4

4.已知(a+b)2=m,(a-b)2=n,则ab等于( )
A、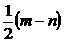 B、
B、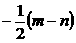 C、
C、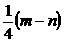 D、
D、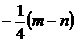
3.若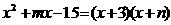 ,则
,则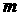 的值为
( )
的值为
( )
A.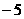 B.5 C.
B.5 C.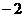 D.2
D.2
2.计算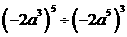 的结果是( )
的结果是( )
A、-2 B、2 C、4 D、-4
1.下列计算中,运算正确的有几个( )
(1) a5+a5=a10 (2) (a+b)3=a3+b3 (3) (-a+b)(-a-b)=a2-b2 (4) (a-b)3= -(b-a)3
A、0个 B、1个 C、2个 D、3个
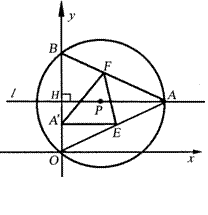
19.如图,已知直线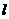 ⊥OB,P点在
⊥OB,P点在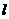 上,以P为圆心,OP长为半径作⊙P交
上,以P为圆心,OP长为半径作⊙P交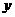 轴的正方向于B点,交
轴的正方向于B点,交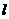 于A点.已知
于A点.已知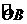 的度数是120°,且OB=2+
的度数是120°,且OB=2+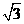 ,连接AB、AO,再将△OAB折叠,使点A落在边OB上,记为A′,折痕为EF.
,连接AB、AO,再将△OAB折叠,使点A落在边OB上,记为A′,折痕为EF.
(1)求证,△AOB是等边三角形,并求出圆心P的坐标,
(2)当A'E∥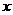 轴时,求点
轴时,求点 和E坐标;
和E坐标;
(3)当A'E∥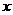 轴,且抛物线
轴,且抛物线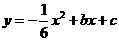 经过点
经过点 和E时,求抛物线与
和E时,求抛物线与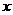 轴的交点的坐标;
轴的交点的坐标;
 (4)当点
(4)当点 在OB上运动但不与点O、B重合时,能否使△A'EF成为直角三角形?若能,请求出此时点
在OB上运动但不与点O、B重合时,能否使△A'EF成为直角三角形?若能,请求出此时点 的坐标;若不能,请你说明理由.
的坐标;若不能,请你说明理由.
18.如图,已知20×20的网络中每个小正方形的边长均为1个单位长度,等腰直角三角形ABC的腰长为4个单位长度,△ABC从点A与点M重合的位置开始,以每秒1个单位长度的速度先向下平移,当BC边与网络的底部重合时,继续以同样的速度向右平移,当点C与点P重合时,△ABC停止运动.设运动时间为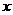 秒,△QAC的面积为
秒,△QAC的面积为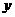 .问:当
.问:当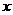 为何值时,
为何值时,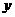 取得最大值和最小值?最大值和最小值各是多少?
取得最大值和最小值?最大值和最小值各是多少?


17.(1)如图( ),它是一个多么漂亮的图案啊!请你在这个图案中确定一个基本图形,然后说出这个基本图形经过怎样的变换便可得到图(
),它是一个多么漂亮的图案啊!请你在这个图案中确定一个基本图形,然后说出这个基本图形经过怎样的变换便可得到图( );
);
(2)如图(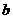 ),将它分成,△OAB、△OBC、△OCD等三个等边三角形(包含三角形内部所有图形).
),将它分成,△OAB、△OBC、△OCD等三个等边三角形(包含三角形内部所有图形).
①探究:△OAB怎样变换可以得到△OBC?△OBC怎样变换可以得到△OCD?
 △OAB怎样变换可以得到△OCD?
△OAB怎样变换可以得到△OCD?
②思考:对称与旋转有何关系?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com