
题目列表(包括答案和解析)
6.[解析]这是一个集几何、代数知识于一体的综合题,既能考查学生的创造性思维品质,又能体现学生的实际水平和应变能力,其解题策略是“动”中求“静”,“一般”中见“特殊”,抓住要害,各个击破.
[答案]解:(1)36;(2)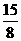 秒;
秒;
(3)当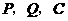 三点构成直角三角形时,有两种情况:
三点构成直角三角形时,有两种情况:
①当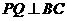 时,设
时,设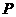 点离开
点离开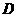 点
点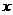 秒,
秒,
作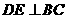 于
于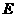 ,
,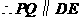 .
.
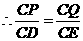 ,
,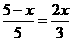 ,
,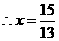 .
.
 当
当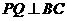 时,
时,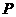 点离开
点离开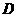 点
点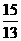 秒.
秒.
②当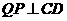 时,设
时,设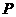 点离开
点离开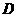 点
点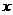 秒,
秒,
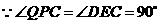 ,
,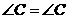 .
.
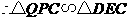 .
.
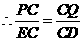 .
.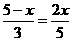 .
.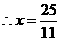 .
.
 当
当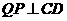 时,点
时,点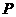 离开点
离开点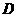
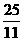 秒.
秒.
由①②知,当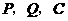 三点构成直角三角形时,点
三点构成直角三角形时,点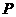 离开点
离开点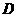
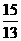 秒或
秒或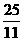 秒.
秒.
5.[解析]该题所蕴涵的知识量较大,并以动态形式,着重考查了四边形、三角形、相似形、平面直角坐标系、二次函数、不等式组等知识点,且解法思路多样化,易于发展学生的各种思维能力。
[答案]解:(1)(4,0),(0,3);
(2) 2,6;
(3) 当0<t≤4时,OM=t.
由△OMN∽△OAC,得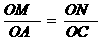 ,
,
∴ ON=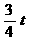 ,S=
,S=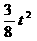 .
.
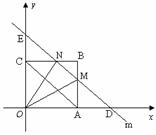
当4<t<8时,
如图,∵ OD=t,∴ AD= t-4.
方法一:由△DAM∽△AOC,可得AM=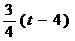 ,∴ BM=6-
,∴ BM=6-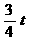 .
.
由△BMN∽△BAC,可得BN=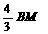 =8-t,∴
CN=t-4.
=8-t,∴
CN=t-4.
S=矩形OABC的面积-Rt△OAM的面积- Rt△MBN的面积- Rt△NCO的面积
=12-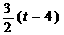 -
-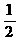 (8-t)(6-
(8-t)(6-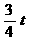 )-
)-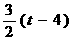
=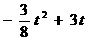 .
.
方法二:易知四边形ADNC是平行四边形,∴ CN=AD=t-4,BN=8-t.
由△BMN∽△BAC,可得BM=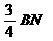 =6-
=6-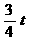 ,∴ AM=
,∴ AM=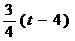 ,以下同方法一.
,以下同方法一.
(4) 有最大值.
方法一:当0<t≤4时,∵ 抛物线S=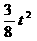 的开口向上,在对称轴t=0的右边,
S随t的增大而增大,
的开口向上,在对称轴t=0的右边,
S随t的增大而增大,
∴ 当t=4时,S可取到最大值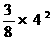 =6;
=6;
当4<t<8时,∵ 抛物线S=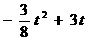 的开口向下,它的顶点是(4,6),∴ S<6.
的开口向下,它的顶点是(4,6),∴ S<6.
综上,当t=4时,S有最大值6.
方法二:
∵ S=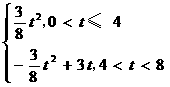
∴ 当0<t<8时,画出S与t的函数关系图像,如图所示.
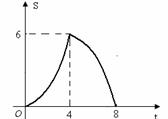
显然,当t=4时,S有最大值6.
4. [答案](1)证明:设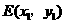 ,
,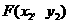 ,
, 与
与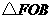 的面积分别为
的面积分别为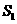 ,
,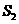 ,
,
由题意得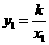 ,
,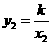 .
.
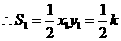 ,
,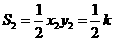 .
.
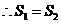 ,即
,即 与
与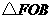 的面积相等.
的面积相等.
(2)由题意知: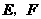 两点坐标分别为
两点坐标分别为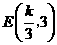 ,
,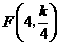 ,
,
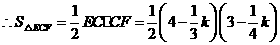 ,
,
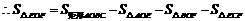
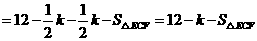

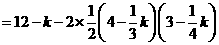
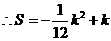 .
.
当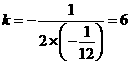 时,
时,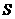 有最大值.
有最大值.
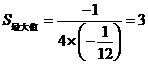 .
.
(3)解:设存在这样的点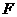 ,将
,将 沿
沿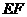 对折后,
对折后,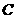 点恰好落在
点恰好落在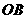 边上的
边上的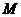 点,过点
点,过点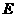 作
作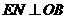 ,垂足为
,垂足为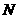 .
.
由题意得: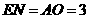 ,
,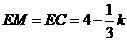 ,
,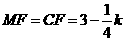 ,
,
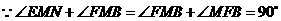 ,
,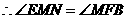 .
.
又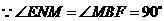 ,
,
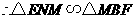 .
.
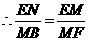 ,
,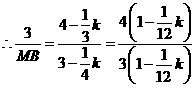 ,
,
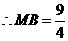 .
.
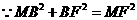 ,
,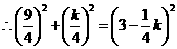 ,解得
,解得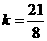 .
.
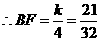 .
.
 存在符合条件的点
存在符合条件的点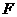 ,它的坐标为
,它的坐标为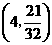 .
.
3.[答案](1)将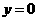 代入
代入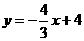 ,得
,得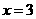 ,
, 点
点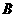 的坐标为
的坐标为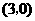 ;
;
将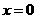 代入
代入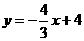 ,得
,得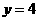 ,
, 点
点 的坐标为
的坐标为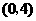 .
.
在 中,
中, ,
,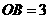 ,
,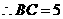 .
.
又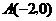 ,
,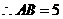 ,
,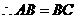 ,
, 是等腰三角形.
是等腰三角形.
(2)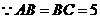 ,故点
,故点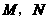 同时开始运动,同时停止运动.
同时开始运动,同时停止运动.
过点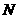 作
作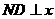 轴于
轴于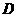 ,
,
则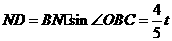 ,
,
①当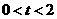 时(如图甲),
时(如图甲),
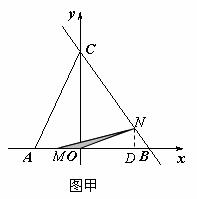
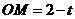 ,
,
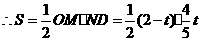
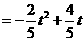 .
.
当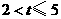 时(如图乙),
时(如图乙),
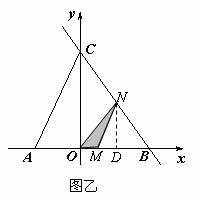
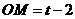 ,
,
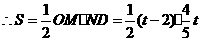
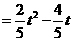 .
.
(注:若将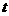 的取值范围分别写为
的取值范围分别写为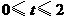 和
和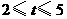 也可以)
也可以)
②存在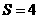 的情形.
的情形.
当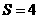 时,
时,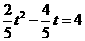 .
.
解得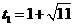 ,
,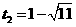 (不合题意,舍去).
(不合题意,舍去).
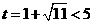 ,故当
,故当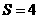 时,
时,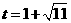 秒.
秒.
③当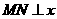 轴时,
轴时,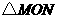 为直角三角形.
为直角三角形.
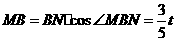 ,又
,又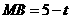 .
.
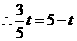 ,
,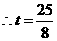 .
.
当点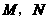 分别运动到点
分别运动到点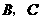 时,
时,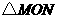 为直角三角形,
为直角三角形,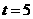 .
.
故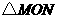 为直角三角形时,
为直角三角形时,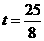 秒或
秒或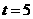 秒.
秒.
2.[解析]本题是双动点问题,解题时需要用运动和变化的眼光去观察和研究问题,挖掘运动、变化的全过程,并特别关注运动与变化中的不变量、不变关系或特殊关系,动中取静,静中求动。
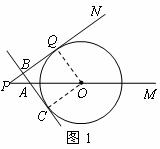
[答案]解:(1)连接 .
.
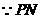 与
与 相切于点
相切于点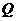 ,
,
 ,即
,即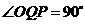 .
.
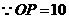 ,
,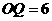 ,
,
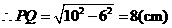 .
.
(2)过点 作
作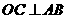 ,垂足为
,垂足为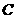 .
.
 点
点 的运动速度为5cm/s,点
的运动速度为5cm/s,点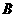 的运动速度为4cm/s,运动时间为
的运动速度为4cm/s,运动时间为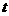 s,
s,
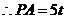 ,
,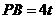 .
.
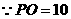 ,
,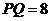 ,
,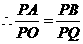 .
.
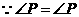 ,
,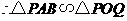 .
.
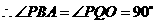 .
.
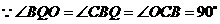 ,
,
 四边形
四边形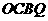 为矩形,
为矩形,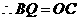 .
.
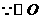 的半径为6,
的半径为6,
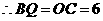 时,直线
时,直线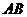 与
与 相切.
相切.
①当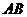 运动到如图1所示的位置.
运动到如图1所示的位置.
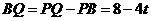 .
.
由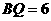 ,得
,得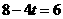 .解得
.解得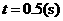 .
.
②当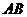 运动到如图2所示的位置.
运动到如图2所示的位置.
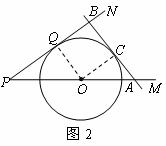
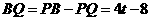 .
.
由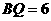 ,得
,得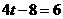 .
.
解得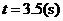 .
.
所以,当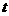 为0.5s或3.5s时直线
为0.5s或3.5s时直线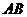 与
与 相切.
相切.
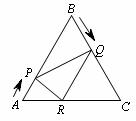
1.[解析]要想证明△ABC与△SBR相似,只要证明其中的两个角相等即可;要想得到TS=PA,只要证明△TPS≌△PFA即可;对于(3),需要建立正方形PTEF的面积y与AP的函数关系式,利用函数的极值来解决.
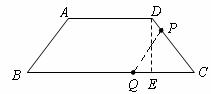
[答案]解:(1)∵RS是直角∠PRB的平分线,∴∠PRS=∠BRS=45°.
在△ABC与△SBR中,∠C=∠BRS=45°,∠B是公共角,
∴△ABC∽△SBR..
(2)线段TS的长度与PA相等.
∵四边形PTEF是正方形,
∴PF=PT,∠SPT+∠FPA=180°-∠TPF=90°,
在Rt△PFA中,∠PFA +∠FPA=90°,
∴∠PFA=∠TPS,
∴Rt△PAF≌Rt△TSP,∴PA=TS.
当点P运动到使得T与R重合时,
这时△PFA与△TSP都是等腰直角三角形且底边相等,即有PA=TS.
由以上可知,线段ST的长度与PA相等.
(3)由题意,RS是等腰Rt△PRB的底边PB上的高,
∴PS=BS, ∴BS+PS+PA=1, ∴PS=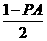 .
.
设PA的长为x,易知AF=PS,
则y=PF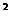 =PA
=PA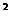 +PS
+PS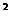 ,得y=x
,得y=x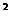 +(
+(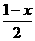 )
)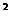 ,
,
即y=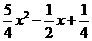 ,(5分)
,(5分)
根据二次函数的性质,当x=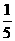 时,y有最小值为
时,y有最小值为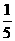 .
.
如图2,当点P运动使得T与R重合时,PA=TS为最大.
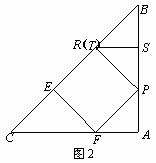
易证等腰Rt△PAF≌等腰Rt△PSR≌等腰Rt△BSR,
∴PA=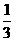 .
.
如图3,当P与A重合时,得x=0.
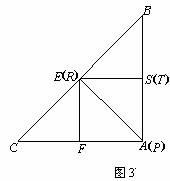
∴x的取值范围是0≤x≤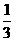 .
.
∴①当x的值由0增大到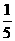 时,y的值由
时,y的值由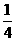 减小到
减小到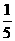
∴②当x的值由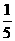 增大到
增大到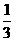 时,y的值由
时,y的值由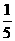 增大到
增大到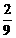
∵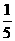 ≤
≤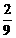 ≤
≤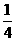 ,∴在点P的运动过程中,
,∴在点P的运动过程中,
正方形PTEF面积y的最小值是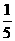 ,y的最大值是
,y的最大值是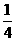 .
.
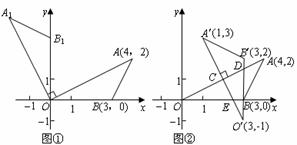
8.(·苏州)课堂上,老师将图①中△AOB绕O点逆时针旋转,在旋转中发现图形的形状和大小不变,但位置发生了变化.当△AOB旋转90°时,得到∠A1OB1.已知A(4,2),B(3,0).
(1)△A1OB1的面积是 ;A1点的坐标为( , );B1点的坐标为( , );
(2)课后,小玲和小惠对该问题继续进行探究,将图②中△AOB绕AO的中点C(2,1)逆时针旋转90°得到△A′O′B′,设O′B′交OA于D,O′A′交x轴于E.此时A′,O′和B′的坐标分别为(1,3),(3,-1)和(3,2),且O′B′经过B点.在刚才的旋转过程中,小玲和小惠发现旋转中的三角形与△AOB重叠部分的面积不断变小,旋转到90°时重叠部分的面积(即四边形CEBD的面积)最小,求四边形CEBD的面积.
(3)在(2)的条件下,△AOB外接圆的半径等于 .
第9课时 动态型问题
7.(·福州)如图,已知△ABC是边长为6cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC匀速运动,其中点P运动的速度是1cm/s,点Q运动的速度是2cm/s,当点Q到达点C时,P、Q两点都停止运动,设运动时间为t(s),解答下列问题:
(1)当t=2时,判断△BPQ的形状,并说明理由;
(2)设△BPQ的面积为S(cm2),求S与t的函数关系式;
(3)作QR//BA交AC于点R,连结PR,当t为何值时,△APR∽△PRQ?
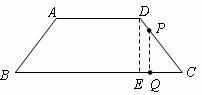
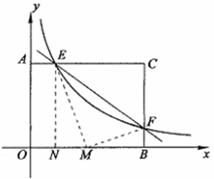
6.(苏州)如图,在等腰梯形 中,
中,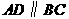 ,
,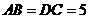 ,
,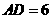 ,
,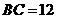 .动点
.动点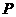 从
从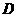 点出发沿
点出发沿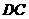 以每秒1个单位的速度向终点
以每秒1个单位的速度向终点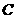 运动,动点
运动,动点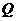 从
从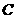 点出发沿
点出发沿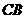 以每秒2个单位的速度向
以每秒2个单位的速度向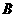 点运动.两点同时出发,当
点运动.两点同时出发,当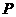 点到达
点到达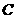 点时,
点时,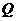 点随之停止运动.
点随之停止运动.
(1)梯形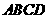 的面积等于
;
的面积等于
;
(2)当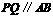 时,P点离开D点的时间等于 秒;
时,P点离开D点的时间等于 秒;
(3)当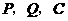 三点构成直角三角形时,
三点构成直角三角形时,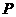 点离开
点离开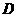 点多少时间?
点多少时间?
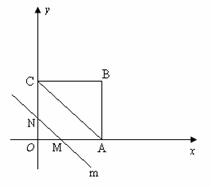
5.(·白银市)如图,在平面直角坐标系中,四边形OABC是矩形,点B的坐标为(4,3).平行于对角线AC的直线m从原点O出发,沿x轴正方向以每秒1个单位长度的速度运动,设直线m与矩形OABC的两边分别交于点M、N,直线m运动的时间为t(秒).
(1) 点A的坐标是__________,点C的坐标是__________;
(2) 当t= 秒或 秒时,MN=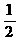 AC;
AC;
(3) 设△OMN的面积为S,求S与t的函数关系式;
(4) 探求(3)中得到的函数S有没有最大值?若有,求出最大值;若没有,要说明理由.








类型之三 开放性动态题
开放性问题的条件或结论不给出,即条件开放或结论开放,需要我们充分利用自己的想像,大胆猜测,发现问题的结论,寻找解决问题的方法,正确选择解题思路。解答开放性问题的思维方法及途径是多样的,无常规思维模式。开放性问题的条件、结论和方法不是唯一的,要对问题充分理解,分析条件引出结论,达到完善求解的目的。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com