
题目列表(包括答案和解析)
4.已知,圆锥的母线长为5cm,高线长是3cm,则圆锥的底面积是( )
A.3πcm2 B.9πcm2 C.16πcm2 D.25πcm2
3.用反证法证明命题“三角形中必有一个内角小于或等于60°”时,首先应假设这个三角形中( )
A.有一个内角大于60° B.有一个内角小于60°
C.每一个内角都大于60° D.每一个内角都小于60°
2.二次函数y=x2的图象向左平移2个单位,得到新的图象的二次函数表达式是( ).
A.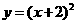 B.
B.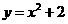 C.
C.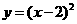 D.
D.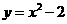
1.下列运算正确的是( )
A.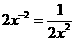 B.
B.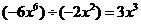 C.
C.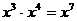 D.
D.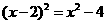
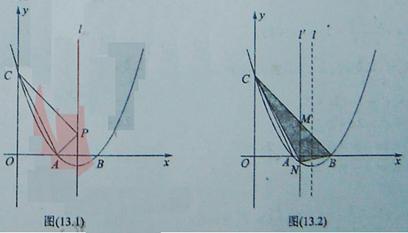
26.(2010四川乐山)如图(13.1),抛物线y=x2+bx+c与x轴交于A,B两点,与y轴交于点C(0,2),连接AC,若tan∠OAC=2.
(1)求抛物线对应的二次函数的解析式;
(2)在抛物线的对称轴l上是否存在点P,使∠APC=90°,若存在,求出点P的坐标;若不存在,请说明理由;
(3)如图(13.2)所示,连接BC,M是线段BC上(不与B、C重合)的一个动点,过点M作直线l′∥l,交抛物线于点N,连接CN、BN,设点M的横坐标为t.当t为何值时,△BCN的面积最大?最大面积为多少?
[答案]解:(1)∵抛物线y=x2+bx+c过点C(0,2). ∴x=2
又∵tan∠OAC=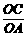 =2, ∴OA=1,即A(1,0).
=2, ∴OA=1,即A(1,0).
又∵点A在抛物线y=x2+bx+2上. ∴0=12+b×1+2,b=-3
∴抛物线对应的二次函数的解析式为y=x2-3x+2
(2)存在
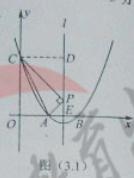
过点C作对称轴l的垂线,垂足为D,如图所示,
∴x=-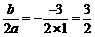 .∴AE=OE-OA=
.∴AE=OE-OA=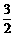 -1=
-1=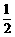 ,∵∠APC=90°,
,∵∠APC=90°,
∴tan∠PAE= tan∠CPD∴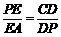 ,即
,即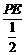
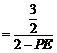 ,解得PE=
,解得PE=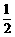 或PE=
或PE=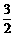 ,
,
∴点P的坐标为(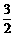 ,
,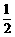 )或(
)或(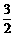 ,
,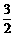 )。(备注:可以用勾股定理或相似解答)
)。(备注:可以用勾股定理或相似解答)
(3)如图,易得直线BC的解析式为:y=-x+2,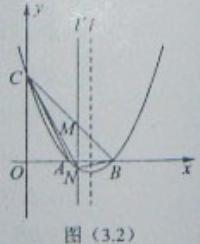
∵点M是直线l′和线段BC的交点,∴M点的坐标为(t,-t+2)(0<t<2)
∴MN=-t+2-(t2-3t+2)=- t2+2t
∴S△BCM= S△MNC+S△MNB=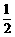 MN▪t+
MN▪t+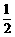 MN▪(2-t)
MN▪(2-t)
=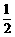 MN▪(t+2-t)=MN=- t2+2t(0<t<2),
MN▪(t+2-t)=MN=- t2+2t(0<t<2),
∴S△BCN=- t2+2t=-(t-1)2+1
∴当t=1时,S△BCN的最大值为1。
备注:如果没有考虑的取值范围,可以不扣分)
25. (2010四川乐山)在△ABC中,D为BC的中点,O为AD的中点,直线l过点O.过A、B、C三点分别做直线l的垂线,垂足分别是G、E、F,设AG=h1,BE=h2,CF=h3.
(1)如图(12.1),当直线l⊥AD时(此时点G与点O重合).求证:h2+h3= 2h1;
(2)将直线l绕点O旋转,使得l与AD不垂直.
①如图(12.2),当点B、C在直线l的同侧时,猜想(1)中的结论是否成立,请说明你的理由;
②如图(12.3),当点B、C在直线l的异侧时,猜想h1、h2、h3满足什么关系.(只需写出关系,不要求说明理由)


[答案]25.(1)证明:∵BE⊥l,GF⊥l,
∴四边形BCFE是梯形.
又∵GD⊥l,D是BC的中点,
∴DG是梯形的中位线,
∴BE+CF=2DG.
又O为AD的中点,∴AG=DG,
∴BE+CF=2AG.
即h2+h3= 2h1.
(2)成立.
证明:过点D作DH⊥l,垂足为H,
∴∠AGO=∠DHO=Rt∠,∠AOG=∠DOH,OA=OD,
∴△AGO≌△DHO,
∴DH=AG.
又∵D为BC的中点,由梯形的中位线性质,
得2 DH=BE+CF,即2 AG =BE+CF,
∴h2+h3= 2h1成立.
(3)h1、h2、h3满足关系:h2-h3= 2h1.
(说明:(3)问中,只要是正确的等价关系都得分)
24.(2010四川乐山)从甲、乙两题中选做一题。如果两题都做,只以甲题计分.
题甲:若关于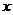 的一元二次方程
的一元二次方程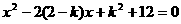 有实数根
有实数根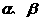 .
.
(1) 求实数k的取值范围;
(2)
设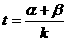 ,求t的最小值.
,求t的最小值.
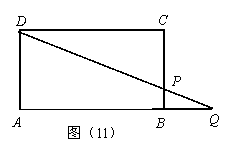

题乙:如图(11),在矩形ABCD中,P是BC边上一点,连结DP并延长,交AB的延长线于点Q.
(1) 若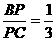 ,求
,求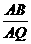 的值;
的值;
(2) 若点P为BC边上的任意一点,求证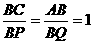 .
.
我选做的是_______题.
[答案]题甲
解:(1)∵一元二次方程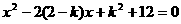 有实数根
有实数根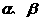 ,
,
∴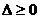 , ………………………………………………………………………2分
, ………………………………………………………………………2分
即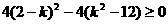 ,
,
解得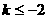 .……………………………………………………………………4分
.……………………………………………………………………4分
(3)由根与系数的关系得: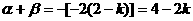 , ………………… 6分
, ………………… 6分
∴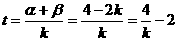 , …………………………………………7分
, …………………………………………7分
∵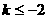 ,∴
,∴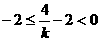 ,
,
∴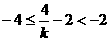 ,
,
即t的最小值为-4. ………………………………………………………10分
题乙
(1)解:四边形ABCD为矩形,
∵AB=CD,AB∥DC,………………………………………………………………1分
∴△DPC ∽△QPB, ………………………………………………………………3分
∴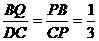 ,
,
∴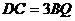 ,
,
∴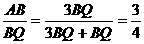 . ………………………………………………………5分
. ………………………………………………………5分
(2)证明:由△DPC ∽△QPB,
得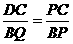 ,……………………………………………………………………6分
,……………………………………………………………………6分
∴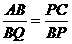 ,……………………………………………………………………7分
,……………………………………………………………………7分
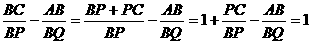 .…………………………10分
.…………………………10分
|
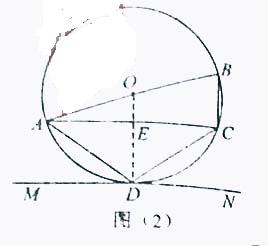
23、(2010四川乐山)如图(10)AB是⊙O的直径,D是圆上一点,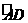 =
=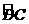 ,连结AC,过点D作弦AC的平行线MN。
,连结AC,过点D作弦AC的平行线MN。
(1)求证明人:MN是⊙O的切线;
(2)已知AB=10,AD=6,求弦BC的长。
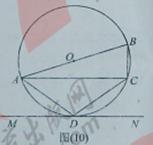
[答案](1)证明:连结OD,交AC于E,如图(2)所示,
因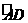 =
=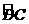 ,所以OD⊥AC 又AC∥MN,所以OD⊥MN
,所以OD⊥AC 又AC∥MN,所以OD⊥MN
所以MN是是⊙O的切线
(2)解:设OE=x,因AB=10,所以OA=5 ED=5-x
又因AD =6 在直角三角形OAE和直角三角形DAE中,因OA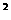 -OE
-OE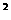 =AE
=AE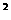 -ED
-ED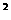 ,
,
所以5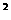 -x
-x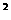 =6
=6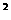 -(5-x)
-(5-x)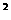 解得x=
解得x=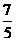
因AB 是⊙O的直径,所以∠ACB=90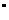 所以OD∥BC
所以OD∥BC
所以OE是△ABC的中位线,所以BC=2OE=2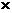
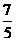 =
=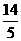
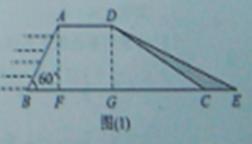
22、(2010四川乐山)水务部门为加强防汛工作,决定对程家山水库进行加固。原大坝的横断面是梯形ABCD,如图(9)所示,已知迎水面AB的长为10米,∠B=60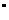 ,背水面DC的长度为10
,背水面DC的长度为10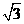 米,加固后大坝的横断面为梯形ABED。若CE的长为5米。
米,加固后大坝的横断面为梯形ABED。若CE的长为5米。
(1)已知需加固的大坝长为100米,求需要填方多少立方米;
(2)求新大坝背水面DE的坡度。(计算结果保留根号)

[答案]解:(1)分别过A、D作AF⊥BC,DG⊥BC,垂点分别为F、G,如图(1)所示
在Rt△ABF中,AB=10米,∠B=60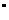 。所以sin∠B=
。所以sin∠B=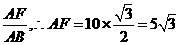
DG=5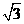
所以S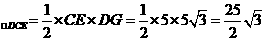
需要填方:100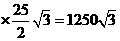 (立方米)
(立方米)
(2)在直角三角形DGC中 ,DC=10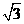 ,
,
所以GC=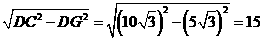
所以GE=GC+CE=20
所以坡度i=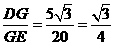
答:(1)需要土石方1250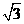 立方米。(2)背水坡坡度为
立方米。(2)背水坡坡度为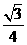
21. (2010四川乐山)某校对八年级(1)班全体学生的体育作测试,测试成绩分为优秀、良好、合格和不合格四个等级,根据测试成绩绘制的不完整统计图如下:
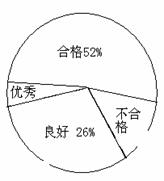 八年级(1)班体育成绩频数分布表 八年级(1)班体育成绩扇形统计图
八年级(1)班体育成绩频数分布表 八年级(1)班体育成绩扇形统计图
|
等级 |
分值 |
频数 |
|
优秀 |
90-100分 |
? |
|
良好 |
75-89分 |
13 |
|
合格 |
60-74分 |
? |
|
不合格 |
0-59分9 |
|
根据统计图表给出的信息,解答下列问题:
(1) 八年级(1)班共有多少名学生?
(2) 填空:体育成绩为优秀的频数是 ,为合格的频数是 ;
(3) 从该班全体学生的体育成绩中,随机抽取一个同学的成绩,求达到合格以上(包含合格)的概率.
[答案]解:(1)由题意得:13÷26%=50;
即八年级(1)班共有50名学生.
(2)2, 26;
(3)随机抽取一个同学的体育成绩,达到合格以上的概率为:
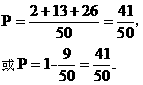
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com