
题目列表(包括答案和解析)
5.理解实数概念,掌握实数的加、减、乘、除、乘方、开方等运算的法则(在引入无理数概念的基础上,建 立实数的概念;再学习实
立实数的概念;再学习实 数的基本运算,并明确有关运算性质的推广和运用;不涉及繁难的纸笔计算)。
数的基本运算,并明确有关运算性质的推广和运用;不涉及繁难的纸笔计算)。
4.引进无理数,经历扩展数的概念的过程;建立实数与数轴上的点的一一对应关系。体验坐标思想和辩证观点。
3.理解开方及方根的意义。
2.掌握比较有理数大小的方法。体会数形结合思想。
1.理解有理数以及相反数、倒数、绝对值等概念,会用数轴上的点表示有理数;学习负数的运算,经历确立有理数的加、减、乘、除、乘方运算法则的过程,并归纳有关运算性质;能灵活运用这些法则和性质进行计算(对有理数的笔算,不出现繁难复杂的问题,重在掌握有理数运算的法则、性质以及运算顺序。有理数的运算性质包括;加法、乘法运算的交换律和结合律,乘法对加法的分配律,加与减、乘与除的互逆性,数0和1的特性等)。
六年级第二学期:第五章 有理数(15课时)
七年级第二学期:第十二章 实数(12课时)
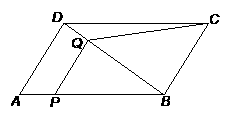
25.在平行四边形ABCD中,AB=5,AD=3,sinA=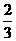 ,点P是AB上一动点
,点P是AB上一动点 ,(点P不与点A、点B重合),过点P作PQ∥AD交BD于Q,连结CQ,设AP 的长为x,四边形QPBC的面积为y.
,(点P不与点A、点B重合),过点P作PQ∥AD交BD于Q,连结CQ,设AP 的长为x,四边形QPBC的面积为y.
(1)计算平行四边形ABCD的面积;
(2)写出y关于x的函数解析式,并指出自变量x的取值范围;
 (3)是否存在实数x,使得
(3)是否存在实数x,使得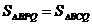 ?如果存在,求出x的值;如果不存在,请说明理由.
?如果存在,求出x的值;如果不存在,请说明理由.
24.抛物线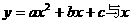 轴交于点A(2,0),B(4,0),与
轴交于点A(2,0),B(4,0),与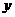 轴交于点C,已知直线
轴交于点C,已知直线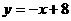 经过点C.
经过点C.
(1)求这个二次函数的解析式;
(2)过点A作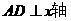 ,与直线
,与直线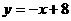 交于点D,如以AD为一条边作平行四边形,使平行四边形的另两个顶点E在抛物线
交于点D,如以AD为一条边作平行四边形,使平行四边形的另两个顶点E在抛物线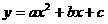 上,顶点F在直线
上,顶点F在直线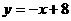 上,求点E、F的坐标.
上,求点E、F的坐标.
23.如图,在梯形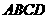 中,
中,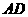 ∥
∥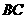 ,∠
,∠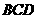 =90°,
=90°,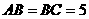 ,
,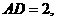
 (1)求
(1)求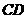 的长; (2)若∠
的长; (2)若∠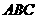 的平分线交
的平分线交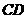 于点
于点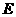 ,连结
,连结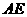 ,求∠
,求∠ 的正切值.
的正切值.
22.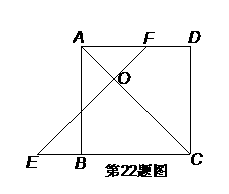 如图,已知在正方形ABCD中,E为CB延长线上一点,F在AD边上,且BE=DF,EF与AC交于点O.求证:△OEC为等腰直角三角形.
如图,已知在正方形ABCD中,E为CB延长线上一点,F在AD边上,且BE=DF,EF与AC交于点O.求证:△OEC为等腰直角三角形.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com