
题目列表(包括答案和解析)
6.给出以下判断:(1)线段的中点是线段的重心
(2)三角形的三条中线交于一点,这一点就是三角形的重心
(3)平行四边形的重心是它的两条对角线的交点
(4)三角形的重心是它的中线的一个三等分点
那么以上判断中正确的有( )
(A)一个 (B)两个 (C)三个 (D)四个
5.有一组数据3、5、7、a、4,如果它们的平均数是5,那么这组数据的方差是( )
(A)2 (B)5 (C)6 (D)7
4.若a、b为实数,且满足|a-2|+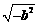 =0,则b-a的值为( )
=0,则b-a的值为( )
(A)2 (B)0 (C)-2 (D)以上都不对
3.今年某市约有108000名应届初中毕业生参加中考,按四舍五入保留两位有效数字,108000用科学计数法表示为( )
(A)0.10×106 (B)1.08×105 (C)0.11×106 (D)1.1×105
2.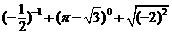 的值为( )
的值为( )
(A)-1 (B)-3 (C)1 (D)0
1.计算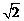 sin45°的结果等于( )
sin45°的结果等于( )
(A)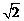 (B)1 (C)
(B)1 (C)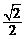 (D)
(D)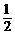
24.(12分)如图,在直角坐标系中,已知点A(-1,0)、B(0,2),动点P沿过B点且垂直于AB的射线BM运动,其运动的速度为每秒1个单位长度,射线BM与x轴交于点C.
(1)求点C的坐标.
(2)求过A、B、C三点的抛物线的解析式.
(3)若点P开始运动时,点Q也同时从C点出发,以点P相同的速度沿x轴负方向向点A运动,t秒后,以P、Q、C为顶点的三角形为等腰三角形(点P到点C时停止运动,点Q也同时停止运动),求t的值.
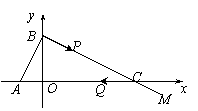 (4)在(2)(3)的条件下,当CQ=CP时,求直线OP与抛物线的交点坐标.
(4)在(2)(3)的条件下,当CQ=CP时,求直线OP与抛物线的交点坐标.
23.(10分)如图,一面利用墙,用篱笆围成的矩形花圃ABCD的面积为Sm2,平行于墙的BC边长为xm.
(1)若墙可利用的最大长度为10m,篱笆长为24m,花圃中间用一道篱笆隔成两个小矩形,求S与x之间的函数关系式.
(2)在(1)的条件下,围成的花圃的面积为45m2时,求AB的长.能否围成面积比45m2更大的花圃?如果能,应该怎样围?如果不能,请说明理由.
(3)若墙可利用最大长度为40m,篱笆长77m,中间用n道篱笆隔成小矩形,且当这些小矩形为正方形和x为正整数时,请直接写出一组满足条件的x、n的值.


22.(10分)工程师有一块长AD=12分米,宽AB=8分米的铁板,截去长AE=2分米、AF=4分米的直角三角形,在余下的五边形中,截得矩形MGCH,其中点M在线段EF上.
(1)若截得矩形MGCH的面积为70平方分米,求矩形MGCH的长与宽.
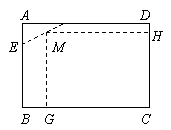 (2)当EM为多少时,矩形MGCH的面积最大?并求此时矩形的周长.
(2)当EM为多少时,矩形MGCH的面积最大?并求此时矩形的周长.
21.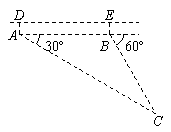 (8分)如图,一艘潜艇在海面下500mA点处测得俯角为30º前下方的海底C处有黑匣子信号发出,继续在同一深度直线航行4000m后再次在B点处测得俯角为60º前下方的海底C处有黑匣子信号发出,求海底黑匣子C点距离海面的深度(结果保留根号).
(8分)如图,一艘潜艇在海面下500mA点处测得俯角为30º前下方的海底C处有黑匣子信号发出,继续在同一深度直线航行4000m后再次在B点处测得俯角为60º前下方的海底C处有黑匣子信号发出,求海底黑匣子C点距离海面的深度(结果保留根号).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com