
题目列表(包括答案和解析)
 根据题意可得
20x+10y=110
根据题意可得
20x+10y=110
30x+10=20y-------------------------------------------------------------------------3分
 解这个方程组得
x=3
解这个方程组得
x=3
y=5---------------------------------------------------------------------------------4分
答:甲种笔记本的单价是3元,乙种笔记本的单价是5元.-----------------------------------5分
(2)设本次购买乙种笔记本m个,则甲种笔记本(2m-10)个.----------------------------6分
根据题意可得 3(2m-10)+5m≤320--------------------------------------------------------------8分
解这个不等式得m≤31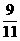 --------------------------------------------------------------------------9分
--------------------------------------------------------------------------9分
因为m为正整数,所以m的最大整数值为31
答:本次乙种笔记本最多购买31个.------------------------------------------------------------10分
20.解:(1) 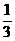 ----------------------------------------------------------------------------------------3分
----------------------------------------------------------------------------------------3分
 第二次 第二次第一次 |
-1 |
2 |
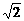 |
|
-1 |
(-1, -1 ) |
(-1, 2 ) |
(-1,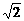 ) ) |
|
2 |
(2, -1) |
(2, 2 ) |
(2,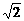 ) ) |
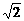 |
(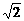 ,-1) ,-1) |
(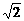 ,2
) ,2
) |
(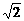 , ,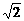 ) ) |
(2)由列表得
---------------7分或画树形图得

 第一次 -1
2
第一次 -1
2 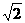
第二次 -1 2 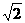 -1 2
-1 2 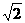 -1 2
-1 2 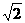
积 1 -2 -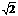 -2 4
2
-2 4
2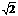 -
-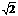 2
2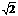 2-----------------------------------------7分
2-----------------------------------------7分
从列表或树形图可以看出,所有可能出现的结果相同,共有9种,其中积是无理数的只
4种,分别是-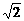 ,2
,2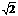 ,-
,-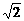 ,2
,2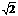 ,∴P(积为无理数)=
,∴P(积为无理数)=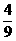 ---------------------------10分
---------------------------10分
五21.(1)50------------------------------------------------------------------------------------------------2分
(2)见统计图-------------------------------------------------------------------------------------------6分
(3)600 --------------------------------------------------------------------------------------------------8分
(4)解:设这个百分数为x.
根据题意可得 600(1+x)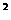 =1176-----------------------------------------------------------------10分
=1176-----------------------------------------------------------------10分
(1+x)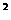 =1.96 解得 x
=1.96 解得 x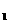 =0.4 x
=0.4 x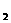 =-2.4(负值不合题意舍去)--------------------12分
=-2.4(负值不合题意舍去)--------------------12分
答:这个百分数为40℅
(注:若(3)的计算结果出现错误,将其代入(4)中,按错误的结果进行解答,只要正确,只扣1分.)
=3+(-8)-9-1+4--------------------------------------------------------------------------------4分
=3-8-9-1+4
=-11--------------------------------------------------------------------------------------------6分
18.解:(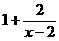 )
)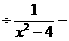 (2x-3)
(2x-3)
=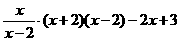 ---------------------------------------------------------3分
---------------------------------------------------------3分
=x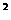 +2x-2x+3
+2x-2x+3
= x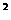 +3----------------------------------------------------------------------------------------5分
+3----------------------------------------------------------------------------------------5分
当x=3时,原式=3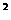 +3=12-----------------------------------------------------------------8分
+3=12-----------------------------------------------------------------8分
26.如图所示,平面直角坐标系中, 抛物线y=ax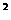 +bx+c 经过 A(0,4)、B(-2,0)、C(6,0).过点A作AD∥x轴交抛物线于点D,过点D作DE⊥x轴,垂足为点E.点M是四边形OADE的对角线的交点,点F在y轴负半轴上,且F(0,-2).
+bx+c 经过 A(0,4)、B(-2,0)、C(6,0).过点A作AD∥x轴交抛物线于点D,过点D作DE⊥x轴,垂足为点E.点M是四边形OADE的对角线的交点,点F在y轴负半轴上,且F(0,-2).
(1)求抛物线的解析式,并直接写出四边形OADE的形状;
(2)当点P、Q从C、F两点同时出发,均以每秒1个长度单位的速度沿CB 、FA方向运动,点P运动到O时P、Q两点同时停止运动.设运动的时间为t秒,在运动过程中,以P、Q、O、M四点为顶点的四边形的面积为S,求出S与t之间的函数关系式,并写出自变量的取值范围;
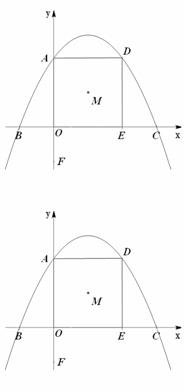 (3)在抛物线上是否存在点N,使以B、C、F、N为顶点的四边形是梯形?若存在,直接写出点N的坐标;不存在,说明理由.
(3)在抛物线上是否存在点N,使以B、C、F、N为顶点的四边形是梯形?若存在,直接写出点N的坐标;不存在,说明理由.
(第26题备用图)
2010年抚顺市初中毕业生学业考试
数学试卷答案及评分标准
25.如图所示,(1)正方形ABCD及等腰Rt△AEF有公共顶点A,∠EAF=90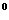 , 连接BE、DF.将Rt△AEF绕点A旋转,在旋转过程中,BE、DF具有怎样的数量关系和位置关系?结合图(1)给予证明;
, 连接BE、DF.将Rt△AEF绕点A旋转,在旋转过程中,BE、DF具有怎样的数量关系和位置关系?结合图(1)给予证明;
(2)将(1)中的正方形ABCD变为矩形ABCD,等腰Rt△AEF变为Rt△AEF,且AD=kAB,AF=kAE,其他条件不变.(1)中的结论是否发生变化?结合图(2)说明理由;
(3)将(2)中的矩形ABCD变为平行四边形ABCD,将Rt△AEF变为△AEF,且∠BAD=∠EAF= ,其他条件不变.(2)中的结论是否发生变化?结合图(3),如果不变,直接写出结论;如果变化,直接用k表示出线段BE、DF的数量关系,用
,其他条件不变.(2)中的结论是否发生变化?结合图(3),如果不变,直接写出结论;如果变化,直接用k表示出线段BE、DF的数量关系,用 表示出直线BE、DF形成的锐角
表示出直线BE、DF形成的锐角 .
.
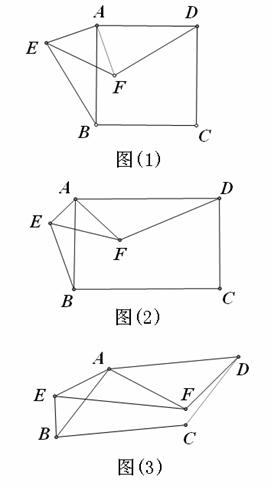
(第25题图)
24.某服装厂批发应季T恤衫,其单价y(元)与批发数量x(件)(x为正整数)之间的函数关系如图所示.
(1)直接写出y与x的函数关系式;
(2)一个批发商一次购进200件T恤衫,所花的钱数是多少元?(其他费用不计);
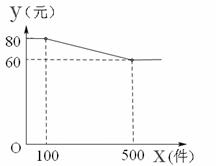 (3) 若每件T恤衫的成本价是45元,当10O<X≤500件 ( x为正整数)时,求服装厂所获利润w(元)与x(件)之间的函数关系式,并求一次批发多少件时所获利润最大,最大利润是多少?
(3) 若每件T恤衫的成本价是45元,当10O<X≤500件 ( x为正整数)时,求服装厂所获利润w(元)与x(件)之间的函数关系式,并求一次批发多少件时所获利润最大,最大利润是多少?
(第24题图)
23.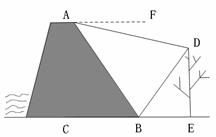 星期天,小强去水库大坝游玩,他站在大坝上的A处看到一棵大树的影子刚好落在坝底的B处(点A与大树及其影子在同一平面内),此时太阳光与地面成60
星期天,小强去水库大坝游玩,他站在大坝上的A处看到一棵大树的影子刚好落在坝底的B处(点A与大树及其影子在同一平面内),此时太阳光与地面成60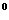 角.在A处测得树顶D的俯角为15
角.在A处测得树顶D的俯角为15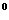 .如图所示,已知AB与地面的夹角为 60
.如图所示,已知AB与地面的夹角为 60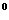 ,AB为8米.请你帮助小强计算一下这颗大树的高度? (结果精确到1米 .参考数据
,AB为8米.请你帮助小强计算一下这颗大树的高度? (结果精确到1米 .参考数据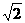 ≈1.4
≈1.4 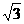 ≈1.7)
≈1.7)
(第23题图)
22.如图所示,在Rt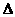 ABC中,∠C=90
ABC中,∠C=90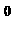 ,∠BAC=60
,∠BAC=60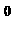 ,AB=8.半径为
,AB=8.半径为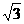 的⊙M与射线BA相切,切点为N,且AN=3.将Rt
的⊙M与射线BA相切,切点为N,且AN=3.将Rt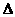 ABC顺时针旋转120
ABC顺时针旋转120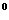 后得到Rt
后得到Rt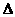 ADE,点B、C的对应点分别是点D、E.
ADE,点B、C的对应点分别是点D、E.
(1)画出旋转后的Rt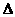 ADE;
ADE;
(2)求出Rt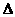 ADE
的直角边DE被⊙M截得的弦PQ的长度;
ADE
的直角边DE被⊙M截得的弦PQ的长度;
(3)判断Rt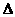 ADE的斜边AD所在的直线与⊙M的位置关系,并说明理由.
ADE的斜边AD所在的直线与⊙M的位置关系,并说明理由.
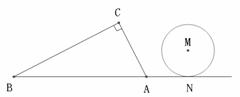

(第22题图)
21.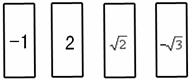 有4张不透明的卡片,除正面写有不同的数字-1、2、
有4张不透明的卡片,除正面写有不同的数字-1、2、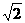 、-
、-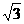 外,其他均相同.将这4张卡片背面向上洗匀后放在桌面上.
外,其他均相同.将这4张卡片背面向上洗匀后放在桌面上.
(1)从中随机抽取一张卡片,上面的数据是无理数的概率是多少?
(2)若从中随机抽取一张卡片,记录数据后放回.重新洗匀后,
再从中随机抽取一张,并记录数据.请你用列表法或画树形图
法求两次抽取的数据之积是正无理数的概率.
(第21题图)
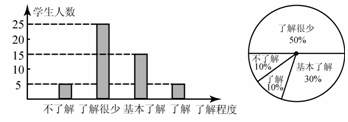
20.2010年5月1日上海世博会召开了,上海世博会对我国在政治、经济、文化等方面的影响很大.某校就同学们对上海世博会的了解程度,随机抽取了部分学生进行问卷调查,并根据收集的信息进行了统计,绘制了下面尚不完整的统计图.根据统计图中所提供的信息解答下列问题:
(1)该校参加问卷调查的学生有________名;
(2)补全两个统计图;
(3)若全校有1500名学生,那么该校有多少名学生达到基本了解以上(含基本了解)的程度?
(4)为了让更多的学生更好的了解世博会,学校举办了两期专刊.之后又进行了一次调查,结果全校已有1176名学生达到了基本了解以上(含基本了解)的程度.如果每期专刊发表之后学生达到基本了解以上(含基本了解)的程度增长的百分数相同,试求这个百分数.
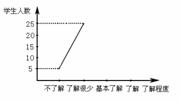

(第20题图)
19.某校团委为了教育学生,开展了以感恩为主题的有奖征文活动,并为获奖的同学颁发奖品.小红与小明去文化商店购买甲、乙两种笔记本作为奖品,若买甲种笔记本20个,乙种笔记本10个,共用110元; 且买甲种笔记本30个比买乙种笔记本20个少花10元.
(1)求甲、乙两种笔记本的单价各是多少元?
(2)若本次购进甲种笔记本的数量比乙种笔记本的数量的2倍还少10个,且购进两种笔记本的总数量不少于80本,总金额不超过320元.请你设计出本次购进甲、乙两种笔记本的所有方案.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com