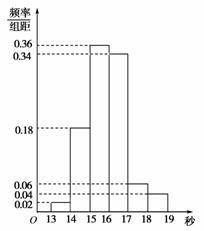
4．某班50名学生在一次百米测试中，成绩全部介于13秒与19秒之间，将测试结果按如下方式分成六组；第一组，成绩大于等于13秒且小于14秒；第二组，成绩大于等于14秒且小于15秒；……第六组，成绩大于等于18秒且小于等于19秒，如图所示，是按上述分组方法得到的频率分布直方图，设成绩小于17秒的学生人数占全部总人数的百分比为x，成绩大于等于15秒且小于17秒的学生人数为y，则从频率分布直方图中可分析出x和y分别为(　)

A．0.9,35　 　　　　　　　　　　　　　　　　　　　 B．0.9,45

C．0.1,35　 　　　　　　　　　　　　　　　　　　　 D．0.1,45

[解析]　P(x<17)＝1－P(17≤ξ≤19)＝1－(0.06×1+0.04×1)＝0.9，即

x＝0.9.y＝(0.34+0.36)×1×50＝35人．

[答案]　A

3．设随机变量ξ服从标准正态分布N(0,1)，已知Φ(－1.96)＝0.025，则P(|ξ|<1.96)等于(　)

A．0.025　 　　　　　　　　　　　　　　　　　　　 B．0.050

C．0.950　 　　　　　　　　　　　　　　　　　　　 D．0.975

[解析]　Φ(－1.96)＝1－Φ(1.96)＝0.025，

∴Φ(1.96)＝0.975，

P(|ξ|<1.96)＝Φ(1.96)－Φ(－1.96)

＝0.975－0.025＝0.95.

[答案]　C

2．(2008年安徽高考题)设两个正态分布N(μ₁，σ)(σ₁>0)和N(μ₂，σ)(σ₂>0)的密度函数图象如图所示，则有(　)

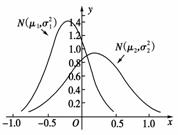
A．μ₁<μ₂，σ₁<σ₂　 　　　　　　　　　　　　　 B．μ₁<μ₂，σ₁>σ₂

C．μ₁>μ₂，σ₁<σ₂　 　　　　　　　　　　　　　 D．μ₁>μ₂，σ₁>σ₂

[解析]　根据正态分布函数F(x)＝e图象关于直线x＝μ对称，而σ²＝Dξ，其大小表示变量集中程度，值越大，数据分布越广，图象越胖；值越小，数据分布越集中，图象越廋，因此选A.

[答案]　A

1．(2008年陕西)某林场在树苗30 000棵，其中松树苗4 000棵，为调查树苗的生长情况，采用分层抽样的方法抽取一个容量为150的样本，则样本中松树苗的数量为(　)

A．30　 　　　　　　　　　　　　　　　　　　　　　 B．25

C．20　 　　　　　　　　　　　　　　　　　　　　　 D．15

[解析]　由题意，样本中松树苗的数量为×150＝20.

[答案]　C

12．某商场经销某商品，根据以往资料统计，顾客采用的付款期数ξ的分布列为

商场经销一件该商品，采用1期付款，其利润为200元；分2期或3期付款，其利润为250元；分4期或5期付款，其利润为300元．η表示经销一件该商品的利润．

(1)求事件A：“购买该商品的3位顾客中，至少有1位采用1期付款”的概率P(A)；

(2)求η的分布列及数学期望Eη.

[解析]　(1)由题意可知每一位顾客不采用1期付款的概率为0.6，记A的对立事件“购买该商品的3位顾客中，都不采用1期付款”为，

则P()＝0.6³＝0.216，∴P(A)＝1－P()＝0.784.

(2)由题意可知η可以取200,250,300，分布列如下

Eη＝200×0.4+250×0.4+300×0.2＝240.

11．(2010年九江模拟)2008年北京奥运会乒乓球男子单打比赛中，我国选手马琳、王皓、王励勤包揽了三块奖牌，通过对以往队内战绩的统计，三人实力相当，即在一局比赛中，每人战胜对手的概率均为0.5.

(1)若王皓和王励勤之间进行三局比赛，求王励勤恰好胜两局的概率．

(2)若马琳和王励勤之间进行一场比赛(7局4胜制)，设所需局数为ξ，求随机变量ξ的分布列及数学期望．

[解析]　(1)王励勤胜两局的概率为

P＝C()²·＝；

(2)马琳和王励勤进行比赛有两种结果，即马琳胜和王励勤胜两种情况：

ξ的取值为4,5,6,7；

当ξ＝4时，概率

P＝C()⁴+C()⁴＝；

当ξ＝5时，概率

P＝C()³··+C()³··＝；

当ξ＝6时，概率

P＝C()³()²·+C()³·()²·＝；

当ξ＝7时，概率

P＝C·()³·()³·+C()³()³·＝.

∴随机变量ξ的分布列为：

∴Eξ＝4×+5×+6×+7×＝.

10．(2010年江门模拟)袋中有红、白两种颜色的小球共7个，它们除颜色外完全相同，从中任取2个，都是白色小球的概率为.甲、乙两人不放回地从袋中轮流摸取一个小球，甲先取，乙后取，然后甲再取，……，直到两人中有一人取到白球时即停止．每个小球在每一次被取出的机会是均等的，用ξ表示游戏停止时两人共取小球的次数．

(1)求P(ξ＝4)；

(2)求Eξ.

[解析]　(1)设袋中原有白球n个，

由题意知：＝，

即n(n－1)＝6，

解得n＝3，n＝－2(舍去)．

P(ξ＝4)＝＝.

(2)由题意可知，ξ的可能取值为1、2、3、4、5，

直接计算得P(ξ＝1)＝，

P(ξ＝2)＝＝，P(ξ＝3)＝＝，

P(ξ＝4)＝，P(ξ＝5)＝＝，

所以Eξ＝1×+2×+3×+4×+5×＝2.

9．若p为非负实数，随机变量ξ的概率分布列如下表，则Eξ的最大值为________，Dξ的最大值为________.

[解析]　Eξ＝p+1≤(0≤p≤)；Dξ＝－p²－P+1≤1.

[答案]　1

8．抛掷一枚硬币，出现正面向上记1分，出现反面向上记2分，若一共抛出硬币4次，且每一次抛掷的结果相互之间没有影响，则总得分ξ的期望Eξ＝________.

[解析]　抛掷4次可能出现的结果是：一正三反，二正二反，三正一反，四正，四反，其对应的分数为7,6,5,4,8，所以ξ的取值为4、5、6、7、8.

设对应概率的值分别为h₄、h₅、h₆、h₇、h₈.

则ξ的分布列为

h₄＝C⁴＝1×＝；

h₅＝C³＝4×＝；

h₆＝C²²＝6×；

h₇＝C³＝4×＝；

h₈＝C⁴＝；

Eξ＝4×+5×+6×6×+7×+8×＝6.

[答案]　6

7．随机变量ξ的分布列如下：

其中a，b，c成等差数列．若Eξ＝，则Dξ的值是________．

[解析]　由a+c＝2b，又a+b+c＝1，Eξ＝，

则a+c＝，c－a＝，得a＝，b＝，c＝.

Dξ＝(－1－)²×+(0－)²×+(1－)²×＝.

[答案]