
题目列表(包括答案和解析)
2.收集一些社会生活中普遍使用的函数模型(指数函数、对数函数、幂函数)的实例,了解函数模型的广泛应用。
1.使用计算工具,比较指数函数、对数函数以及幂函数增长差异;结合实例体会直线上升、指数爆炸、对数增长等不同函数类型增长的含义。
4.注意参数的分类讨论
例4 设A={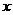 ∣
∣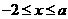 },B={
},B={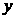 ∣
∣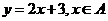 },C={
},C={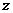 ∣
∣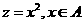 },且
},且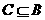 ,求实数
,求实数 的取值范围.
的取值范围.
解析:∵ A={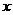 ∣
∣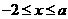 },
},
 ∴ B={
∴ B={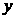 ∣
∣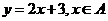 }={
}={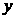 ∣
∣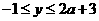 }.
}.
①当 时,C={
时,C={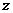 ∣
∣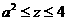 }. ∵
}. ∵ 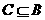 ,
,
∴  ,解得
,解得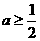 ,这与
,这与 矛盾.
矛盾.
②当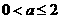 时,C={
时,C={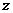 ∣
∣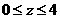 }. ∵
}. ∵ 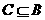 ,
,
∴  ,解得
,解得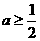 . ∴
. ∴ 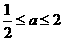 .
.
③当 时,C={
时,C={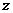 ∣
∣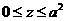 }. ∵
}. ∵ 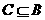 ,
,
∴ 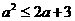 ,解得-1
,解得-1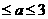 . ∴
. ∴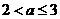 .
.
综上得,实数 的取值范围是
的取值范围是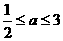 .
.
评注:对含有参数的问题,求解时常常要对其中的参数进行分类讨论,这也是集合中体现出来的重要数学思想之一.
3.注意端点值的舍取
例3 已知集合A={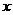 ∣
∣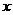 ≥4,或
≥4,或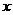 <-5},B={
<-5},B={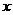 ∣
∣ +1≤
+1≤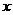 ≤
≤ +3},若A∪B=A,求
+3},若A∪B=A,求 得取值范围.
得取值范围.
错解:由A∪B=A得 B A.
A.
∴ +3≤-5,或
+3≤-5,或 +1≥4,解得
+1≥4,解得 ≤-8,或
≤-8,或 ≥3.
≥3.
分析:上述解法忽视了等号能否成立,事实上,当 =-8时,不符合题意;当
=-8时,不符合题意;当 =3时,符合题意,故正确结果应为
=3时,符合题意,故正确结果应为 <-8,或
<-8,或 ≥3.
≥3.
评注:在求集合中字母取值范围时,要特别注意该字母在取值范围的边界能否取等号,否则会导致解题结果错误.
2.注意题中的隐含条件
例2设全集U={2,3,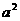 +2
+2 -3},A={∣2
-3},A={∣2 -1∣,2},
-1∣,2}, ={5},
={5},
求实数 的值.
的值.
错解:∵ ={5},∴ 5
={5},∴ 5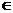 S且 5
S且 5 A,从而,
A,从而,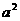 +2
+2 -3=5,解得
-3=5,解得 =2,或
=2,或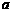 =-4.
=-4.
分析 导致错误的原因是没有考虑到隐含条件,因为U是全集,所以A U.当
U.当 =2时,∣2
=2时,∣2 -1∣=3
-1∣=3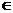 S,符合题意;当
S,符合题意;当 =-4时,∣2
=-4时,∣2 -1∣=9
-1∣=9 S,不符合题意;故
S,不符合题意;故 =2.
=2.
评注:在解有关含参数的集合时,需要进行验证结果是否满足题设条件,包括隐含条件.
1.注意空集的特殊作用
例1 已知集合A={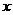 ∣
∣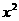 +(
+( +2)
+2)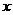 +1=0,
+1=0, 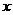
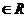 }.B={
}.B={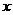 ∣
∣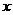 >0}, 若
>0}, 若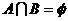 ,求
,求 的取值范围.
的取值范围.
解析:由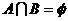 知,A中的元素为非正数,即方程
知,A中的元素为非正数,即方程 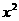 +(
+( +2)
+2)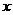 +1=0只有非正数解.
+1=0只有非正数解.
∴ 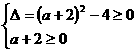 解得
解得 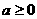
实际上,这个结果是不完整的,上述解法只注意到A为非空解集,当A为空集时,仍满足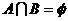 . 当A=
. 当A=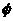 时,
时,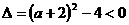 ,解得-4<
,解得-4< <0,
<0,
综上可得 :  >-4
>-4
评注:空集是任何非空集合的子集,且A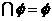 , A
, A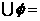 A., 在解有关含有参数的集合题时,忽视了空集的特殊性,就会造成解题解结果的残缺不全.
A., 在解有关含有参数的集合题时,忽视了空集的特殊性,就会造成解题解结果的残缺不全.
对于一些有明显特征的集合,可以将集合中的元素一一列举出来,然后从中寻找解题方法。
例7集合A={x|x=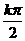 +
+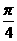 , k∈Z},B={x|x=
, k∈Z},B={x|x=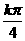 +
+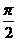 k∈Z}则有( )
k∈Z}则有( )
A.A = B B.A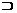 B C. A
B C. A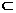 B
B  D.A∩B =φ
D.A∩B =φ
解:分别取k=···-2,-1,0,1,2···得A={···-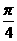 ,
,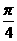 ,
,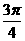 ,
,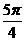 ,
,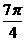 ···} ,B={···
···} ,B={···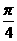 ,
,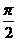 ,
,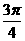 ,π,
,π,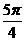 ,
,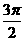 ,
,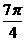 ···}
···}
易得A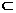 B 故选C.
B 故选C.
例8已知全集U=N,集合A={x|x=2n,n∈N},集合B={x|x = 4n,n∈N},则( )
A.U= A∪B B.U= C A∪B
C.A∪C
A∪B
C.A∪C B
D.C
B
D.C A∪C
A∪C B
B
解:用列举法有:集合A={2,4,6,8,···};集合B={4,8,12,16···}
所以C B={1,2,3,5,6,7,9···},于是有U=
A∪C
B={1,2,3,5,6,7,9···},于是有U=
A∪C B,故选C.
B,故选C.
在解集合问题时,用常用性质求解,往往快捷迅速,如C A∪C
A∪C B = C
B = C ( A∩B),C
( A∩B),C A∩C
A∩C B=C
B=C ( A∪B),φ∩A=φ, φ∪A=A,φ
( A∪B),φ∩A=φ, φ∪A=A,φ A,集合A中有n个元素其子集个数为2
A,集合A中有n个元素其子集个数为2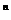 ,真子集个数为2
,真子集个数为2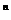 -1等。
-1等。
例4 设全集U={a,b,c,d,e},集合A={a,c,d},B={b,d,e},那么C A∩C
A∩C B =( )。
B =( )。
A.φ B.{d} C.{a,c} D.{b,c}
解:C A∩C
A∩C B= C
B= C ( A∪B)= C
( A∪B)= C U=φ,故选A.
U=φ,故选A.
例5设全集U={0,1,2,3,4},集合A={0,1,2,3},集合B={2,3,4},则C A∪C
A∪C B = ( )
B = ( )
A.{0} B.{0,1} C.{0,1,4} D.{0,1,2,3,4}
解:因为A∩B={2,3},C A∪C
A∪C B= C
B= C ( A∩B)= {0,1,4}故选C.
( A∩B)= {0,1,4}故选C.
例6 集合A={x|0≤x<3且x∈N}的真子集个数为( )
A.16 B.8 C.7 D.4
解:集合A={0,1,2}共3个元素,其真子集个数为2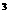 -1。故选C.
-1。故选C.
由实数与数轴上的点对应关系,可以用数轴上的点或区间表示数集,从而直观形象地分析问题和解决问题。
例1设集合A={x||4x-1|≥9,x∈R},B={x|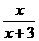 ≥0 ,x∈R }则A∩B =
( )
≥0 ,x∈R }则A∩B =
( )
A.(-3,-2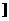 B.(-3,-2
B.(-3,-2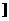 ∪[0,
∪[0,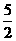 ]
]
C.(-∞,-3) ∪(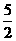 , +∞
, +∞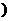 D.(-∞,-3) ∪[
D.(-∞,-3) ∪[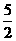 ,+∞
,+∞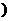
解:集合A={x||4x-1|≥9,x∈R}={x|x≥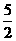 或x≤-2,x∈R},集合B={x|
或x≤-2,x∈R},集合B={x|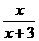 ≥0 ,x∈R }={x|x <-3或x ≥0},把集合A
≥0 ,x∈R }={x|x <-3或x ≥0},把集合A
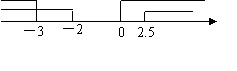 和集合B所表示的范围在数轴上表示出来,
和集合B所表示的范围在数轴上表示出来,
可得A∩B =(-∞,-3) ∪[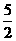 ,+∞
,+∞
例2集合A={
x∈R|x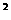 -x-6
< 0},B={
x∈R||x-2| < 2},则A∩B =___________。
-x-6
< 0},B={
x∈R||x-2| < 2},则A∩B =___________。
 解:A={ x∈R|x
解:A={ x∈R|x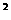 -x-6
< 0}={x|-2
< x < 3}, B={ x∈R||x-2| < 2}={x|0 < x
< 4}.把集合A和集合B所表示的范围在
-x-6
< 0}={x|-2
< x < 3}, B={ x∈R||x-2| < 2}={x|0 < x
< 4}.把集合A和集合B所表示的范围在
|
|
|
|

 数轴上表示出来,可得A∩B ={x|0 < x < 3}
数轴上表示出来,可得A∩B ={x|0 < x < 3}
例3集合A={x|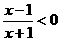 },B ={x||x-b| < a},若“a = 1”是“A∩B =φ”的充分条件,则b 的取值范围可以是( )
},B ={x||x-b| < a},若“a = 1”是“A∩B =φ”的充分条件,则b 的取值范围可以是( )
. A.-2≤b< 0. B.0< b≤2。 C.-3 < b<-1 D.-1≤b< 2
解:集合A={x|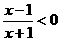 }={x|-1<x <1},当 “a =1“ 时B ={x||x-b| < 1}= {x|-1 + b < x <1 + b}
}={x|-1<x <1},当 “a =1“ 时B ={x||x-b| < 1}= {x|-1 + b < x <1 + b}
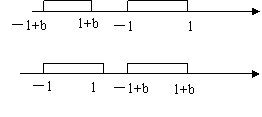
以上两个图都A∩B =φ,因为“a = 1”是“A∩B =φ”的充分条件,由图可得-1≤b< 2,故选D。
12.袋中有8个白球,2个黑球,从中随机地连续取3次球,每次取1个,求:
(1)不放回抽样时,取到黑球的个数ξ的分布列;
(2)放回抽样时,取到黑球个数η的分布列.
[解析] (1)不放回抽样时,取到的黑球个数ξ可能的取值为0,1,2,
且有:p(ξ=0)==,p(ξ=1)==,
p(ξ=2)==,
所以ξ的分布列为:
|
ξ |
0 |
1 |
2 |
|
P |
|
|
|
(2)有放回抽样时,取到的黑球数η可能的取值为0,1,2,3.又由于每次抽到黑球的概率均为=,3次取球可以看成3次独立重复试验,
即η-B,
p(η=k)=Ck3-k
=Ck3-k,(k=0,1,2,3).
其分布列
|
ξ |
0 |
1 |
2 |
3 |
|
P |
|
|
|
|
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com