3．　 制作多个同样大小的任意锐角三角形，拼一拼，看它们能铺满地面吗？任意三角形可以吗？把图形画在下面的方框内。

2．试一试

用几种正多边形拼在一起，也能铺满地面，你能通过生活中的细心观察，举出几个例子吗？画出图形。

[智力拓展]

1．用一批相同的多边形地面砖来铺满地面，要求各个顶点要聚在一起，且砖与砖之间不留空隙，则下列图形不能选用的是(　　 )

A．正三角形　 B．正六边形　C．正方形　D．正十二边形

2．　 难点是理解能否拼成几何图形的根据。

[难点突破]

通过本节课的学习，我们知道了，用一种正多边形铺地面时，只有________、________、__________三种能铺满地面，你能说出其中的数学道理吗？

[知识与生活]

走在马路上或是公园的小路上，你有没有发现地上铺的地面砖有的虽然很简单，但却能拼出美丽的图案来？构成图案的每一块地砖都是正多边形吗？你能否自己设计一种正多边形地砖，而且能拼出美丽的图案。

[同步提升]

[必备功底]

1．　 本节的重点是了解可以拼在一起的几何图案。

8．4正多边形拼地板

[教材解读]

要使学生通过正多边形拼地板的问题，理解正三角形、正方形、正六边形乃至任意三角形、四边形能镶嵌平面的理由，从中体验应用数学知识解决实际问题的过程，学会必要的数学方法。

[重点再现]

7．探索规律：四边形有2条对角线；五边形有5条对角线；六边形有9条对角线；七边形有14条对角线，那么n边形有多少条对角线呢？

[数学趣闻连载]　　

　　　　　　　　　　　　 　　剪刀和纸片(三)

“当然！听清楚啊，我用浆糊把纸条的两端粘贴起来，就可以做出长长的纸环。你拿着红色和蓝色的铅笔，沿着纸环的外侧，画一个蓝色的大圆圈，在纸环内侧则画上红线。”

“然后呢？”

“这样就好了。”

我觉得这工作简直太无聊。但我却做不好这简单的工作。本来，我想用蓝铅笔沿着纸环外侧，先画出下道蓝圈，再用红笔画纸环内侧。大概是没注意，我在纸环的两面，都用蓝笔画上了圆圈。因此，我自已也觉得很不好意思。

“你能不能给我另一个纸环？”我停一下又说，“因为我一不小心，就把刚才的纸环画坏了。”

虽然哥哥给我另一个纸环，但我依旧宣告失败。不知道为什么，我在纸环的两面都画了相同的颜色。说真的，我自己也搞不清楚是怎么回事。

“不知道为什么？我明明沿着纸环表面画，没想到又失败了。哥哥，再给我一个纸环好不好？”

“好啊，你尽量拿，这一点纸环，我不会吝啬的。”

读者们猜想结果如何？结果我以在红环的两面画出蓝色，我始终没有使用红笔的机会。这时，我不由双手抱头，开始沉思。

5．　 在六边形ABCDEF中，如图，EF∥BC，AF∥DC，∠F=120⁰，∠A=80⁰，你能算出∠B和∠C的度数吗？并简要说明理由。

[整合互动]

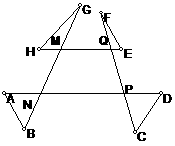
5．红红和兰兰在玩剪纸游戏时，剪出来了这样的一个图形，如图，你能求出∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H的度数吗？

4．一个凸多边形，张明在计算它的内角和，一会儿，张明求得内角和是2400⁰，王刚发现张明在计算过程中少算了一个内角的度数，你能推断一下张明少计算的那个内角的度数吗？这个凸多边形是几边形呢？