3.这两个正多边形分别是五边形和十边形，内角和分别为540°和1440°.(提示：设这两个正多边形的边数分别为n和2n条，根据多边形的内角和公式，可得两正多边形的内角和分别为　　　　　　 和　　　　　　 ，由于两正多边形内角和的度数之比为3∶8，所以)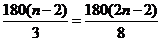

2.因为∠2是△ABC的外角，所以∠2>∠BAC(三角形的外角大于和它不相连的内角).

同理可说明∠BAC>∠1，从而推出∠2>∠1.

1．不符合规定.理由：因为∠BAC、∠ACD与该角组成一个三角形，根据三角形内角和可知这三个角度之和为180°，所以可以求出这个角的度数为81°，故相交所成的角不符合规定.

9.12　 10. 120°

1．50°　 2．4，6　　 3．70°　　 4.9　　 5．3　　 6．135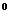　 7．1440　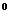 8．52

1．C　 2．A　　 3．C　 4．D　 5．B　 6．D　 7. B　 8．A　 9．A　 10．A

6．如图，在△ABC中，∠BAC=90°，∠B=56°，AD⊥BC，DE∥CA．求∠ADE的度数．

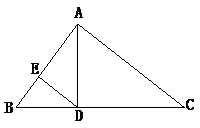
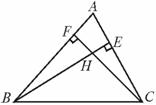
5．在△ABC中，已知∠ABC=66°，∠ACB=54°，BE是AC上的高，CF是AB上的高，H是BE和CF的交点，求∠ABE、∠ACF和∠BHC的度数.

4．在△ABC中AB=AC，AC上的中线BD把三角形的周长分为24cm和30cm的两个部分，求三角形的三边长。

3．两个正多边形的边数之比为1∶2，内角和之比为3∶8，求这两个多边形的边数、内角和.