8.如图7-2-11,已知P是△ABC内一点，试说明：∠BPC＞∠BAC.

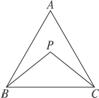
图7-2-11

解：如图，连结AP并延长交BC于点D.

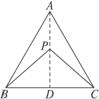
因为∠BPD＞∠BAD,∠DPC＞∠DAC,所以∠BPD+∠DPC＞∠BAD+∠DAC.故∠BPC＞∠BAC.

7.(2010湖北十堰模拟，14)如图7-2-10，已知AB∥CD,∠A=55°,∠C=20°,则∠P=_________.

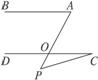
图7-2-10

解析：∵AB∥CD，∴∠A=∠DOP=55°.

∵∠DOP=∠P+∠C(三角形的外角等于与它不相邻的两个内角的和)，

∴∠P=55°-20°=35°.

答案：35°

6.如图7-2-9所示，∠1+∠2+∠3+∠4+∠5=_____________.

解析：通过作辅助线完全可以把它转化为三角形的问题.

方法一：如图，延长CB到D，则由三角形内外角的关系可得∠DCE=∠4+∠5，∠CDE=∠1+∠2，所以由三角形内角和可得∠1+∠2+∠3+∠4+∠5= ∠DCE+∠CDE+∠3=180°.

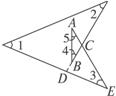
方法二：如图，延长CB到D，则由三角形内外角的关系可得∠ACD=∠CDE+∠3，∠CDE=∠1+∠2，所以∠1+∠2+∠3+∠4+∠5=∠CDE+∠3+∠4+∠5=∠ACD+∠4+∠5 =180°其中方法一是把五个角转到了△CDE中，方法二是把五个角转到了△ABC中.

答案：180°

5.如图7-2-8所示，在△ABC中，∠B的平分线与∠ACB的外角的平分线相交于点E，若∠A=40°，则∠E=_____________.

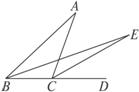
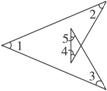
图7-2-8　　　　　 　　　　　　图7-2-9

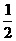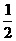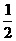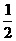解析：由三角形的内外角的关系可得∠ACD=∠A+∠ABC，∠ECD=∠E+∠EBC，由角平分线的定义可得∠ECD=∠ACD，∠EBC=∠ABC，所以∠E=∠ECD-∠EBC= ∠ACD-∠ABC=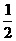∠A=20°.

答案：20°

4.如图7-2-7所示，∠A+∠B+∠C+∠D+∠E+∠F等于(　　 )

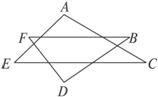
图7-2-7

A.180°　　　　　　　 B.360°　　　　　　 C.540°　　　　　　　 D.720°

解析：∠A,∠E,∠C是△AEC的内角，∠D,∠F,∠B是△DFB的内角，∴∠A+∠B+∠C+ ∠D+∠E+∠F=360°.

答案：B

3.(2010安徽模拟，5)如图7-2-6所示，直线a∥b，点B在直线b上，且AB⊥BC,∠1=55°，则∠2的度数为(　　 )

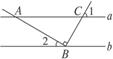
图7-2-6

A.35°　　　　　　 B.45°　　　　　　 C.55°　　　　　　　　 D.125°

解析：∵a∥b，∴∠2=∠CAB(两直线平行，内错角相等).∵∠1=∠ACB(对顶角相等)，

∴∠ACB=55°.∵∠CAB+∠ABC+∠ACB=180°(三角形的内角和等于180°)，

∴∠CAB=180°-90°-55°=35°.

∴∠2=35°.

答案：A

2.已知在△ABC中，∠A=105°，∠B-∠C=15°，则∠B等于(　　 )

A.45°　　　　　　 B.36°　　　　　 C.72°　　　　　　　　 D.144°

解析：由三角形内角和定理可以得到∠A+∠B+∠C=180°，即∠B+∠C=75°，所以可列方程组为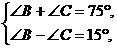解得∠B=45°,∠C=30°.

答案：A

1.已知在△ABC中，∠B=∠C=2∠A，则∠C等于(　　 )

A.45°　　　　　　 B.36°　　　　　 C.72°　　　　　　　　 D.144°

解析：利用设未知数列方程的方法，设∠A=x°,则∠B=∠C=2x°，由三角形内角和定理，得x+2x+2x=180,解得x=36,所以∠C=72°.

答案：C

6.如图7-2-5所示，∠BAF、∠CBD、∠ACE是△ABC的三个外角,

求∠BAF+∠CBD+∠ACE的度数.

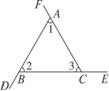
图7-2-5

解：因为三角形的一个外角等于和它不相邻的两个内角的和，所以∠BAF=∠2+∠3，∠CBD=∠1+∠3，∠ACE=∠1+∠2.所以∠BAF+∠CBD+∠ACE=2(∠1+∠2+∠3)=2×180°=360°.

30分钟训练(巩固类训练，可用于课后)

5.已知三角形的三个内角的度数之比为1∶3∶5,求这三个内角的度数.

解：由题意可设三角形三个内角分别为x、3x、5x,所以由三角形的内角和可得x+3x+5x=180°,解得x=20°,所以这三个内角分别为20°,60°,100°.