1．一般三角形与直角三角形证明全等的方法有什么区别与联系？

例1、　　 已知：如图3-82，在△ABC与△AˊBˊCˊ中，CD和CˊDˊ分别是高，并且AC=AˊCˊ，CD=CˊDˊ，∠ACB=AˊCˊBˊ.

求证：△ABC≌△AˊBˊCˊ.

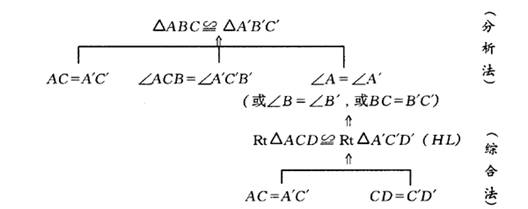
说明：请一名学生口述，教师纠正后板书正确过程.

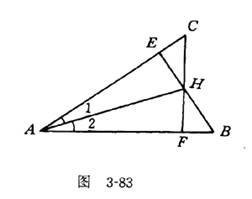
(投影)练习2 如图3-83，AB=AC，CF┵AB于F，BE┵AC于E，CF与BE交于H.求证：(1)AH平分∠ABC；(2)CH=BH；(3)AH┵BC；(4)连结BC与AH的延长线交于D，图中有多少对全等三角形？为什么？(5)交换“AB=AC”与“AH平分∠BAC”，以上命题是否成立？为什么？

说明：(1)通过二次全等证明所需结论，并培养学生逆向思维能力.

(2)通过此题全面复习直角三角形全等的判定方法(SAS，AAS，ASA，HL).

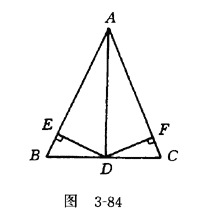
(投影)练习3 已知：如图3-84，AB=AC，AD┸BC于D，DE┸AB于E，DF┸AC于F.求证：DE=DF.

(投影)例3 求证：有一条直角边和斜边上的高对应相等的两个直角三角形全等.

说明：要求学生根据文字叙述画图，分析已知、未知条件，根据直角三角形的判定方法来证明两次全等．

4．叙述公理，强调条件及格式.

教师板书“HL公理”的内容，说明它实际上就是两边及其中一边的对角对应相等，但所对的角是直角，所以它只对直角三角形适用，对一般三角形并不一定成立，因此，在“HL公理”的使用过程中要突出直角三角形这个条件，对于图3-81，在Rt△ABC与Rt△AˊBˊC

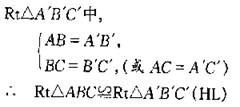
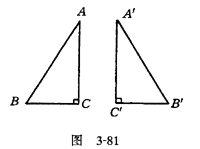
3．画图得出公理.

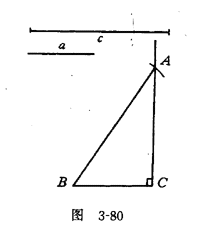
例1　　　　 　如图3-80，已知线段a,c(a<c),画一个Rt△ABC,使∠C=90°，一直角边CB=a,斜边AB=c.

教师应注意启发学生选择合理的画图顺序来确定三角形的三个顶点：

画直角确定顶点C→在直角一边上截取线段a确定B点→以点B为圆心，线段c为半径作弧与另一直角边相交确定点A.

说明：(1)教师按照教材所述，详细板书画法并作图.

(2)着重说明画出的直角三角形存在且唯一，因此，可以作为判定公理，称为“斜边、直角边公理”，简写为“HL”.

2．探求判定直角三角形全等的特殊方法.

(1)　对直角三角形中的两对对应元素进行分类，探求有无判定全等的其它方法.

除练习1的(1)和(2)之外，还有以下两种情况：

①　 两锐角对应相等；

②　 斜边和一直角边对应相等.

(2)对第①句，由教师和学生手中的含30°的直角三角板可说明它不成立，

因此，判定直角三角形全等仍然至少需要一边对应相等.

对第②句，通过画图寻找答案.

3、由于直角三角形与一般三角形相比增加了一个特殊条件--直角，因此，判定直角三角形全等的条件可减弱到两个，“SSS”对直角三角形来说条件多余.

2、由于直角三角形是特殊的三角形，所以一般三角形全等的四种判定方法对直角三角形都适用.

1．可用判定一般三角形全少的方法．

练习1　 判断以下各组直角三角形是否全等，为什么？

(1)　　　　 两直角边对应相等的两个直角三角形；

(2)　　　　 一边和一锐角对应相等的两个直角三角形.

分析：(1)判定两直角三角形全等时，直角相等是一个很重要的隐含条件.

31、解法一：利用平角为180°求得，如图

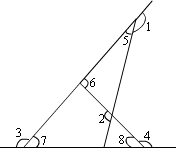
∵∠2＝∠5+∠6，∠6＝∠7+∠8(三角形的一个外角等于和它不相邻的两个内角和)

∴∠1+∠2+∠3+∠4＝∠1+(∠5+∠6)+∠3+∠4

　　　　　＝(∠1+∠5)+(∠7+∠8)+∠3+∠4

　　　　　＝(∠1+∠5)+(∠3+∠7)+(∠8+∠4)(等式性质)

而∠1+∠5＝180°，∠3+∠7＝180°，∠8+∠4＝180° (平角的定义)

∴∠1+∠2+∠3+∠4＝3×180°＝540°

解法二：利用四边形内角和为360°求得，如图

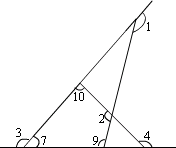
∵∠1＝∠7+∠9，∠4＝∠7+∠10(三角形的一个外角等于和它不相邻的两个内角和)

又∠3＝180°－∠7(平角定义)

∴∠1+∠2+∠3+∠4＝(∠7+∠9)+∠2+(180°－∠7)+(∠7+∠10)

　　　　　＝( ∠7+∠9+∠2+∠10)+180°

　　　　　＝360°+180°

　　　　　＝540°(等式性质)

还有其它多种证法，请去探索

30、分析：

　此题是常见的“频率分布直方图问题”，直方图是横着放置的，识图，读懂题意，善于处理信息和数据是关键.

解：

　(1)根据频率＝，从有关“环境保护”的热线电话为70个，又从图中对应找到频率为35%求本周的热线电话的个数就是求总体个数.

　　　即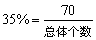，∴本周电话个数有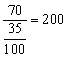(个)

　(2)同理本周“道路交通”问题的电话个数为：

　　 200×20%＝40(个)

答：本周共接到热线电话有200个，有关道路问题的电话有40个.