45. ΔABC中，∠C＝90º，AC＝6，BC＝8，M为BC中点，P是AB上一个动点(可与A、B重合)，若∠MPD＝90º，PD交BC(或　　 其延长线)于D，设BP＝x，y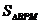＝，问：是否存在这样的点P，使得ΔMPD∽ΔABC？若存在，求x的值；否则，请说明理由。

44. 抛物线y＝ax²+bx+c(a≠0) 图像的最高点的纵坐标是1，试化简代数式|a|+

43.设抛物线y＝－3x²－2kx+k²与双曲线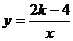在第二象限中一个交点的横坐标为－2，求k的值以及两图像交点的个数。

42. 已知抛物线y＝ax²+bx+c与y轴交于点(0，2)，与x轴两交点的横坐标之和比它们的积的8倍小1，求a的取值范围。

41.. (如图)ΔABC中，∠C＝90º，AC＝BC＝3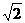，动点P在AB上，过P作PE⊥AC于E，PF⊥BC于F，设CF＝x，问：是否存在这样的点P，使RtΔAEP，RtΔPFB以及矩形ECFP的面积都小于4？

40..(2004,黄冈,11分)心理学家研究发现,一般情况下, 学生的注意力随着老师讲课时间的变化而变化,讲课开始时,学生的注意力逐步增强, 中间有一段时间学生的注意力保持较为理想的状态,随后学生的注意力开始分散.经过实验分析可知, 学生的注意力y随时间t的变化规律有如下关系式:

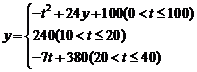
　 (1)讲课开始后第5分钟时与讲课开始后第25分钟时比较, 何时学生的注意力更集中?

　 (2)讲课开始后多少分钟,学生的注意力最集中?能持续多少分钟?

　 　(3)一道数学难题,需要讲解24分钟,为了效果较好,要求学生的注意力最低达到180,那么经过适当安排,老师能否在学生注意力达到所需的状态下讲解完这道题目?

39.(2002,昆明,8分)某广告公司设计一幅周长为12米的矩形广告牌, 广告设计费为每平方米1000元,设矩形一边长为x米,面积为S平方米.

　 　　(1)求出S与x之间的函数关系式,并确定自变量x的取值范围.

　 　　(2)为使广告牌美观、大方,要求做成黄金矩形,请你按要求设计,并计算出可获得的设计费是多少?(精确到元)

38.如图所示,在边长为4的正方形EFCD上截去一角,成为五边形ABCDE, 其中AF=2,BF=1,在AB上取一点P,设P到DE的距离PM=x,P到CD的距离PN=y,试写出矩形PMDN的面积S与x之间的函数关系式.

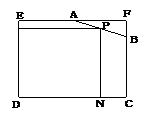
17．(本题14分)已知关于x的一次函数y=mx+3n和反比例函数y=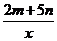的图象都过点(1，-2)，求：

　 (1)一次函数和反比例函数的解析式；(2)两个函数图象的另一个交点的坐标．

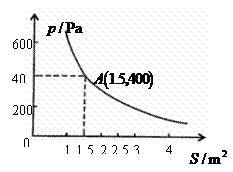
16．(本题12分)某校科技小组进行野外考察，途中遇到一片十几米宽的烂泥湿地．为了安全、迅速通过这片湿地，他们沿着前进路线铺了若干块木块，构筑成一条临时近道．木　板对地面的压强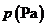是木板面积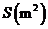的反比例函数，其图象如下图所示．

(1)请直接写出这一函数表达式和自变量取值范围；

(2)当木板面积为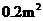时，压强是多少？

(3)如果要求压强不超过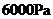，木板的面积至少要多大？