
题目列表(包括答案和解析)
2.如图4所示,已知一次函数y=kx+b(k≠0)的图象与x轴、y 轴分别交于A,B两点,且与反比例函数y=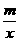 (m≠0)的图象在第一象限交于C点,CD⊥x轴, 垂足为D,若OA=OB=OD=1.
(m≠0)的图象在第一象限交于C点,CD⊥x轴, 垂足为D,若OA=OB=OD=1.
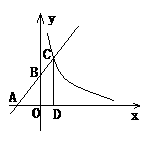 (1)求点A, B, D坐标.
(1)求点A, B, D坐标.
(2)求一次函数和反比例函数的关系式.
(3)根据图象写出一次函数的值大于反比例
函数的值的x的取值范围。(9分)
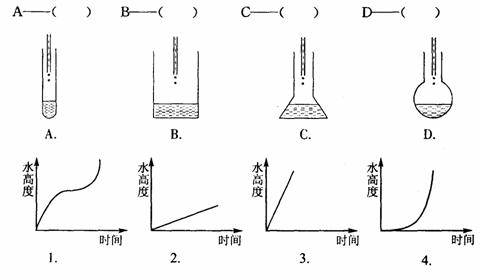
1.水滴进的玻璃容器如下图所示(水滴的速度是相同的),那么水的高度h是如何
随着时间t变化的.请选择匹配的示意图与容器.(4分)
4.某人从A城出发,前往离A城30千米的B城。现在有三种车供他选择:①自行车,其速度为15千米/时;②三轮车,其速度为10千米/时;③摩托车,其速度为40千米/小时。
(1)用哪些车能使他从A城到达B城的时间不超过2小时,请说明理由。
 (2)设此人在行进途中离B城的路程为s千米,行进时间为小时,就(1)所选定的方案,试写出s与t的函数关系式(注明自变量t的取值范围),并在图7所给的平面直角坐标系中画出此函数的图像。
(2)设此人在行进途中离B城的路程为s千米,行进时间为小时,就(1)所选定的方案,试写出s与t的函数关系式(注明自变量t的取值范围),并在图7所给的平面直角坐标系中画出此函数的图像。
附加题: (20 分)
3.农民带上若干千克自产的土豆进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售, 他手中持有的钱数(含备用零钱)y(元)与售出的土豆x(千克)的关系如图所示,结合图象回答下列问题:
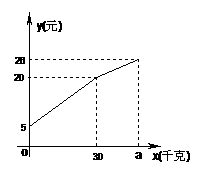 (1)农民自带的零钱是
元。
(1)农民自带的零钱是
元。
(2)试求降价前y与x之间的关系式.
(3)降价后他按每千克0.4元将剩余土豆售完,这时他手中的钱(含备用零钱)是26元,试问他一共带了多少千克土豆?
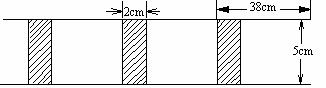
2.将长为38cm,宽为5cm的长方形白纸,按如图所示方法粘合在一起,粘合部分白纸为2cm。
(1)求10张白纸粘合后的长度;
(2)设x张白纸粘合后的总长为ycm,写出y与x的函数关系式。
1. ①当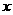 为何值时,
为何值时,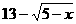 的值最大,最大值是多少?
的值最大,最大值是多少?
②当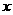 为何值时,
为何值时,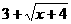 的值最小,最小值是多少?
的值最小,最小值是多少?
3.已知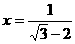 ,
,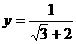 ,求
,求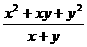 .
.
1.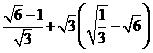 ; 2.
; 2.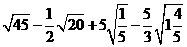 ;
;
10.已知a-2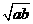 +b=0(a>0,b>0),则
+b=0(a>0,b>0),则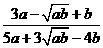 等于 ( )
等于 ( )
A.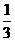 B.
B.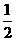 ;
C.
;
C.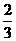 D.
D.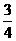
9.把(1-a)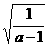 根号外的因式移到根号内,结果是( )
根号外的因式移到根号内,结果是( )
A.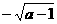 B
B 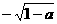 C
C 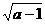 D
D 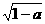
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com