
题目列表(包括答案和解析)
2.已知直角三角形中30°角所对的直角边长是2厘米,则斜边的长是( )
A.2厘米 B.4厘米 C.6厘米 D.8厘米
1.一元二次方程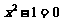 的根为( )
的根为( )
A.x=1 B.x=-1 C.x1=1,x2=-1 D.x1=0,x2=1
4. 一次函数y=kx+b(k≠0)的图象经过点(-2,1)和(4,4)
(1)求它的函数关系式,并画出图象;
(2)P为该函数图象上一点,A为该函数图象与x轴的交点,若S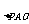 =6,
=6,
 求点P的坐标。
求点P的坐标。
3. 有一个装有进、出水管的容器,单位时间内进、出的水量都是一定的。已知容器的容积为600升,又知单开进水管10分钟可把空容器注满,若同时打开进、出水管,20分钟可把满容器的水放完,现已知水池内有水200升,先打开进水管5分钟后,再打开出水管,两管同时开放,直至把容器中的水放完,则能正确反映这一过程中容器的水量Q(升)随时间t(分)变化的图象是( )

2. 已知点A(2a+3b,-2)和点B(8,3a+2b)关于x轴对称,那么a+b= 。
1.
已知函数y=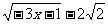 ,则x的取值范围是
。 若x是整数,则此函数的最小值是
。
,则x的取值范围是
。 若x是整数,则此函数的最小值是
。
28. 甲骑自行车、乙骑摩托车沿相同路线由A地到B地,行驶过程中路程与时间的函数关系的图象如右图。 根据图象解决下列问题:
(1) 谁先出发?先出发多少时间?谁先到达终点?先到多少时间?
答: ; ; ; 。
(2) 分别求出甲、乙两人的路程与时间的函数关系式及自变量取值范围?
(3) 在什么时间段内,两人均行驶在途中(不包括起点和终点)?在这一时间段内,请你根据下列情形,分别列出关于行驶时间x的方程或不等式(不化简,也不求解):
① 甲在乙前面;
 ② 甲与乙相遇;
② 甲与乙相遇;
③ 甲在乙后面;
姓名: ,班级 ,学号
拓展试题:(选做,4+4+3+10=20分)
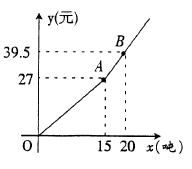
27. 某市选自来水公司为鼓励居民节约用水,采取按月用水量收费办法,若某户居民应交消费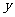 (元)与用水量
(元)与用水量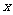 (吨)的函数关系如图所示。分别写出当0≤
(吨)的函数关系如图所示。分别写出当0≤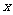 ≤15和
≤15和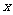 ≥15时,
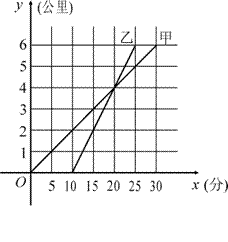
≥15时,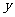 与
与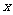 的函数关系式;若某用户该月用水21吨,则应交水费多少元?
的函数关系式;若某用户该月用水21吨,则应交水费多少元?
26.  求直线
求直线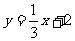 与
与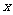 轴和
轴和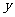 轴的交点,并画出这条直线及求出这条直线与坐标轴围成三角形的面积。
轴的交点,并画出这条直线及求出这条直线与坐标轴围成三角形的面积。
25. 若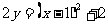 ,且
,且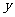 的算术平方根是3,求
的算术平方根是3,求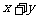 的值。
的值。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com