
题目列表(包括答案和解析)
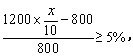 整理,得120x≥840. ∴ x≥7.
整理,得120x≥840. ∴ x≥7.
即至多可打7折才符合题意. (注:1折是指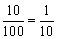 ,∴ x折是指
,∴ x折是指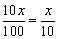 ).
).
12、解:(1)依题意,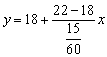 , ∴ y=18+16x(x≥0).
, ∴ y=18+16x(x≥0).
(2)由(1)可知,y表示甲离开A站的距离,即30<y<50.
∴ 30<18+16x<50,解此不等式组,得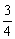 <x<2.
<x<2.
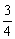 小时=
小时=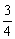 ×60分钟=45分钟.
×60分钟=45分钟.
所以,甲在上午8点45分到10点,行驶在B、C两站之间(不包括B、C两站),下面是甲在B、C两站行驶的路程与时间的函数图象(如图所示).
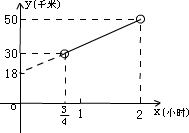
14、解:设学校购买 x 台电脑,甲公司收费为 y甲元,乙公司收费为 y乙元,
∴ y甲 =5800×10+5800×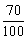 (x-10) , ∴ y甲 =4060x+17400
(x≥11)
y乙 =5800 ×
(x-10) , ∴ y甲 =4060x+17400
(x≥11)
y乙 =5800 ×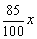 =4930x
=4930x
(1)若 y甲 =y乙,即 4060x+17400=4930x ,∴ x=20 (台)
(2)若 y甲 >y乙,即 4060x+17400>4930x ,∴ x<20 (台)
(3)若 y甲 <y乙,即 4060x+17400<4930x ,∴ x>20 (台)
答:
当购买电脑 20 台时,在甲、乙两公司购买均可,当购买电脑大于 20 台时,到甲公司购买开支较小,当 x<20 台时,有两种情况:①当 0<x ≤ 10 时,甲公司收费是 5800 × 10=58000 (元),而乙公司收费为 5800 ×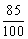 ×10=49300 (元),到乙公司购买开支较小。②当 11 ≤ x<20 时,仍到乙公司购买开支较小 .
×10=49300 (元),到乙公司购买开支较小。②当 11 ≤ x<20 时,仍到乙公司购买开支较小 .
13、解:由①去分母: 6(a-3)<2-a ,∴ 7a<20 , a<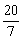 ;
;
由②去分母: a(x-4)<5(x-a) 化简得 (a-5)x<-a ,由①可知 a<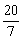 ;
∴ a-5<
;
∴ a-5<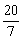 -5 ,即 a-5<-
-5 ,即 a-5<-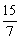 <0 ,
<0 ,
∴ x>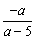 ,即 x>
,即 x>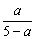 .
.
又∵ x≥1 ,在数轴上可知,要使 x≥1 适合不等式(1),则 3m ≤ 1 ,∴ m ≤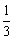 .
.

12、解:若 18 人买普通票则要 10×18=180 (元)现按 20 人的团体票则要 10×0.8×20=160 (元)
∴买 20 人的团体票便宜 180-160=20 (元)设至少要有 x 人购买团体票划算,则应有 10x≥160
∴ x≥16 ∴至少要有 16 人,购买团体票才划算 .
14、烟台大樱桃闻名全国,今年又获丰收,某大型超市从大樱桃生产基地购进一批大樱桃,运输过程中质量损失5%(超市不负责其它费用).
(1)如果超市把售价在进价基础上提高5%,超市是获利还是亏本;
(2)如果超市至少要获得20%的利润,那么大樱桃的售价最低提高百分之几(精确结果0.1%)?
答案:一、BCDCB CABBC
13、光明中学为加强现代信息技术课的教学拟投资建一个初级计算机机房和一个高级计算机机房,每个计算机机房只配置1台教师用机,若干台学生用机,其中初级机房教师用机8000元,学生用机每台3500元;高级机房教师用机11500元,学生用机每台7000元,已知两机房购买计算机的总钱数相等,且每个机房购买计算机的总钱数不小于20万元,也不超过21万元,那么,该校两个机房各应有多少台计算机.
12、公路上依次有A、B、C三个站(如图所示)
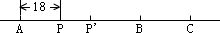
上午8时,甲骑自行车从A、B两站之间且离A站18千米的P点处出发向C站匀速前进,15分钟后到达离A站22千米P'处.
(1)设x小时后,甲离A站y千米,写出用x表示y的关系式;
(2)若A、B间和B、C间的距离,分别是30千米和20千米.
从上午几点几分到几点几分时,甲在B、C两站之间(不包括B、C两站)?并作出甲在B、C之间的函数图象.
11、某种商品的进价为800元,出售时标价为1200元,后来由于商品积压,商品准备打折出售,但要保持利润率不低于5%,则至多打几折.
10、不等式组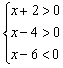 的正整数解的个数有(
)个.
的正整数解的个数有(
)个.
A.1 B.2
C.3 D.4
窗体底端
9、已知一次函数y1=3x+3与y2=-2x+8在同一坐标系中的交点坐标为(1,6),则当y1>y2时,x的取值范围是( )
A.x≥1 B.x=1
C.x<1 D.x>1
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com