6、把16－x⁴分解因式，其结果是(　　　 )

A、(2－x)⁴　　　　　　　　　　 B、(4+x²)( 4－x²)

C、(4+x²)(2+x)(2－x)　　　　 D、(2+x)³(2－x)

5、(－2)¹⁹⁹⁸+(－2)¹⁹⁹⁹等于(　　 )

A、－2¹⁹⁹⁸ B、2¹⁹⁹⁸C、－2¹⁹⁹⁹ D、2¹⁹⁹⁹

4、把多项式－2x⁴－4x²分解因式，其结果是(　　 )

A、2(－x⁴－2x²)　 B、－2(x⁴+2x²)　 C、－x²(2x²+4)　 D、 －2x²(x²+2)

3、把－8m³+12m²+4m分解因式，结果是(　　 )

A、－4m(2m²－3m)　　　　　　 B、－4m(2m²+3m－1)

C、－4m(2m²－3m－1)　　　　 D、－2m(4m²－6m+2)

2、用提提公因式法分解因式5a(x－y)－10b·(x－y)，提出的公因式应当为(　　 )

A、5a－10b　 B、5a+10b　 C 、5(x－y)　　 D、y－x

1、代数式a³b²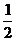－a²b³, 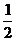a³b⁴+a⁴b³,a⁴b²－a²b⁴的公因式是(　　 )

A、a³b²　 B、a²b²　　 C、a²b³　　 D、a³b³

[教学反思]

本节课在内容安排方面，贯彻了步步深入的原则：提出转化思想-实现转化的手段-探索转化的方向-转化思想的简单评价。在安排上还注意了由简到繁，由易到难与由繁到简，由难到易的结合。在方法上注意了把握好教师指导程度与学生独立活动程度两者的分寸。随着课的深入，学生独立活动的程度在逐渐增加。上述内容是在重点中学中进行教学的。同时在教学过程中教师要关注学生能否利转化思想进行因式分解。

这一节课， 我们学习了运用转化思想解因式分解问题。要使转化思想在处理因式分解问题时获得成功，需要注意三个素：转化的方向清楚；转化的手段有效；因式分解的基本功扎实。运用转化思想处理因式分解，只是众多思路中的一种，它不是唯一的，也不是万能。另外，这种转化思想还可以用来处理其他一些数学问题，以后的学习我们会经常遇到。

师：同学们做得很好，我再出三道难度较大一些的问题，看同学们能不能攻下来。

生：(情绪高涨)

例2：把下列各式因式分解：

(1)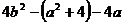　　　　 (2)a(a-4b)+4(b+c)(b－c)

(3)两个奇数的平方差一定能被8整除。

(请三位程度中等的学生板演)

生甲：(1)原式==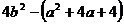

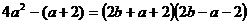
生乙：(2)原式=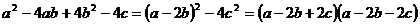

生甲：(3)设两个奇数为2n－1、2n+1则

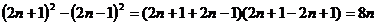
故他能被8整除。

师：同学们认为例2第(3)小题的证法对不对？

(大部分学生认为证法正确，但有学生提出异议)

生：我认为这种证法不对，设两个奇数为2n+1,2n－1，这就等于说它们是两个连续的奇数，但题目并没有说这个两个奇数必须是连续的，因此应该设这两个奇数为2n+1和2m+1。

师：说得很好。如果题目指的是两个连续奇数，那么黑板上的证法是正确的，但现在题目里没有“连续奇数“这个条件，因此上述证明是有问题的，你能说一说你的证法吗？

生：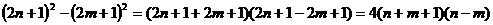

这说明它能被4整除。( 这时答不下去了)

师：如果命题正确的话，应该怎样呢？

生：(n+m+1)(n－m)应该被2整除。

(大家讨论如何证明(n+m+1)(n－m)被2整除。

师：大家研究一下n、m的奇偶性。

生：如果n和m奇偶性相同的话，n－m必是偶数，命题得证；如果n和m有一个为奇数，一个为偶数，那么n+m+1为偶数，命题也成立。

师：对，这题告诉我们，同学们在解题时，除了方法正确以外，还需要有灵活的思路，方能把新旧知识融会贯通，刚才我们处理的两道例题，转化的方向是十分明确的。

我们已经学习了因式分解的哪几种基本方法？

生：提公因式法、公式法(完全平方公式、平方差)。

师：不错，对一个具体的问题，我们往往不能一下判断出应选 用哪一种方法，或应该综合运用哪几种方法来解决。由于不存在一种万能的妙法，我们就需要探索出关于多项式因式分解的一般思路，以帮助我们有效地解决因式分解的问题，下面我们先看一个具体的问题。

例1：把下列各式分解因式

(1)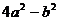　　　　　　　 (2)4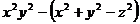

(3)

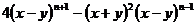
(学生练习，教师巡视，发现学生都能得到正确答案)

生1：(1)题利用平方差公式进行因式分解。

生2：第(2)题可利用平方差公式，再利用完全平方公式和平方差公式进行因式分解。

生3：第(3)题先提公因式，再利用平方差公式进行因式分解。

并上黑板写出完整解答。