11. 设AD=x米，则AB为(10+x)米，AC为(15-x)米，BC为5米，∴(x+10)²+5²=(15-x)²，解得x=2，∴10+x=12(米)

AC²=AB²+BC²=3²+4²=25， ∴ AC=5.

在△ACD中，∵ AC²+CD²=25+12²=169，

而 AB²=13²=169，

∴ AC²+CD²=AB²，∴ ∠ACD=90°．

故S_{四边形ABCD}=S_△ABC+S_△ACD=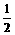AB·BC+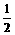AC·CD=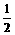×3×4+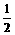×5×12=6+30=36.

10. 解：由勾股定理得AE²=25，EF²=5，

AF²=20，∵AE²= EF² +AF²，

∴△AEF是直角三角形

90°.6.54，提示：先根基勾股定理逆定理得三角形是直角三角形，面积为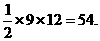7.直角，提示：

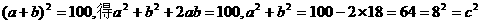；8.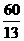，提示：先根据勾股定理逆定理判断三角形是直角三角形，再利用面积法求得；

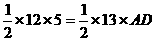18.2勾股定理的逆定理答案：

12. 观察下列勾股数：

第一组：3=2×1+1，　　　　 4=2×1×(1+1)，　　　 5=2×1×(1+1)+1；

第二组：5=2×2+1，　　　　 12=2×2×(2+1)，　　 13=2×2×(2+1)+1；

第三组：7=2×3+1，　　　　 24=2×3×(3+1)，　　 25=2×3×(3+1)+1；

第三组：9=2×4+1，　　　 40=2×4×(4+1)，　　　 41=2×4×(4+1)+1；

……

观察以上各组勾股数的组成特点，你能求出第七组的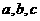各应是多少吗？第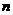组呢？

11. 如图，AB为一棵大树，在树上距地面10m的D处有两只猴子，它们同时发现地面上的

C处有一筐水果，一只猴子从D处上爬到树顶A处，

利用拉在A处的滑绳AC，滑到C处，另一只猴子从D处

滑到地面B，再由B跑到C，已知两猴子所经路程都是15m，

求树高AB.

10.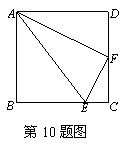 如图，E、F分别是正方形ABCD中BC和CD边上的点，且AB=4，CE=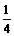BC，F为CD的中点，连接AF、AE，问△AEF是什么三角形？请说明理由.

9. 如图，已知四边形ABCD中，∠B=90°，AB=3，BC=4，CD=12，AD=13，

求四边形ABCD的面积.

8.在三角形ABC中，AB=12，AC=5，BC=13，则BC边上的高为AD=　　　 .

7.已知三角形ABC的三边长为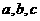满足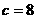，，则此三角形为

　　　 三角形.