
题目列表(包括答案和解析)
1.D;2.△ECD,AB=EC,BC=CD,AC=ED, ∠A=∠E, ∠B=∠ECD, ∠ACB=∠D,3. AE=AC、BC=DE ∠B=∠ADE、∠BAC=∠DAE ;4.B,提示:MQ与NP是对应边,全等三角形的对应边相等;5.B,提示:②③正确,①④没有对应边相等;6.D;7. 95°,提示:全等三角形的对应角相等即∠C=∠D=20°,再根据三角形的内角和定理得∠OAD=95°;8.A,提示:首先要分析、观察两图中的对应部分是什么,然后再根据图形计算阴影部分的面积(全等图形的面积一定相等);9.证明:∵△ABC≌△EBD,∴∠A=∠E,又∵∠AOF=∠EOB,∴∠A+∠AOF=∠E+∠EOB,
又∵∠1=180°-(∠A+∠AOF),∠2=180°-(∠E+∠EOB),∴∠1=∠2.
第二课时答案:
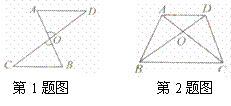
3.如图,已知AC和BD相交于O,且BO=DO,AO=CO,下列判断正确的是( )
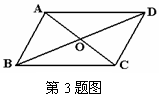 A.只能证明△AOB≌△COD
A.只能证明△AOB≌△COD
B.只能证明△AOD≌△COB
C.只能证明△AOB≌△COB
D.能证明△AOB≌△COD和△AOD≌△COB
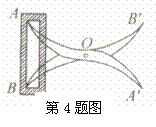
&4.如图所示,将两根钢条AA′、BB′的中点O连在一起,使AA′、BB′可以绕着点O自由转动,就做成一个测量工件,则A′B′的长等于内槽AB,那么判定△OAB≌△OA′B′的理由是( )
 A.SAS
B.ASA
C.SSS
D.AAS
A.SAS
B.ASA
C.SSS
D.AAS
※5.如图所示,已知AD∥BC,AD=BC,
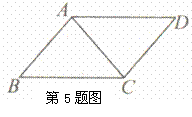 试说明AB∥CD
试说明AB∥CD
#6. 如图,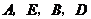 在同一直线上,在
在同一直线上,在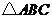 与
与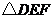 中,
中,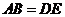 ,
,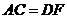 ,
,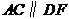 .
.
(1)求证: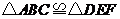 ;
;
 (2)你还可以得到的结论是 (写出一个即可,不再添加其它线段,不再标注或使用其它字母).
(2)你还可以得到的结论是 (写出一个即可,不再添加其它线段,不再标注或使用其它字母).

#7. 如图,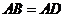 ,
,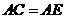 ,
,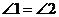 ,
,
求证: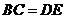
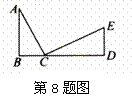
※8.已知AB⊥CD与B,ED⊥BC与D,AB=CD、BC=DE,
求证:AC⊥CE
第一课时答案:
5.已知如图所示AB、CD相交于O,且AD=CB,AB=CD.
求证∠A=∠C
 第三课时11.2.2三角形全等的条件(SAS)及其应用
第三课时11.2.2三角形全等的条件(SAS)及其应用
&1.如图所示,若线段AB、CD互相平分交于点O,
则下列结论错误的是( )
A.AD=BC B. ∠C=∠D
C.AD∥BC D.OB=OC
&2.如图所示,BD、AC相交于点O,若OA=OD,用“SAS”说明△AOB≌△DOC,还需要添加 .
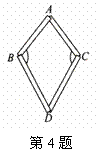
3. 李明用四根木条钉成一个四边形,如图所示,其中木条AB=AC,BD=CD,李明说:拉动A、D两点,∠B和∠C的大小会发生变化,但∠B和∠C一直是相等,李明的说法对吗?为什么?
李明用四根木条钉成一个四边形,如图所示,其中木条AB=AC,BD=CD,李明说:拉动A、D两点,∠B和∠C的大小会发生变化,但∠B和∠C一直是相等,李明的说法对吗?为什么?
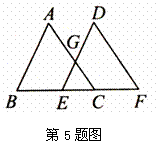
#4. 如图所示,点B、E、C、F、在同一直线上,
BE=CF,AB=DE,AC=DF,AC和DE相交于点G,
 试说明∠EGC=∠D.
试说明∠EGC=∠D.
2. 如图所示,已知,在△ABC和△DCB中,AC=DB,若不增加任何字母与辅助线,要使△ABC≌△DCB,则还需增加一个条件是__ .
5.下列说法中正确的个数为( )
①所有的等边三角形都全等;②两个全等三角形的最大边是对应边;③两个全等三角形的对应角相等;④对应角相等的三角形是全等三角形.
A.1 B.2 C.3 D.4
&6. 如图,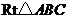 沿直角边
沿直角边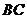 所在的直线向右平移得到
所在的直线向右平移得到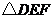 ,下列结论中错误的是( )
,下列结论中错误的是( )
A.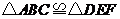 B.
B.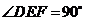 C.
C.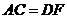 D.
D.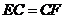
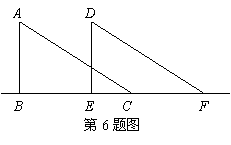
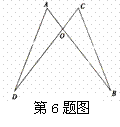
※7. 如图,若△OAD≌△OBC,且∠0=65°,∠C=20°,则∠OAD= .
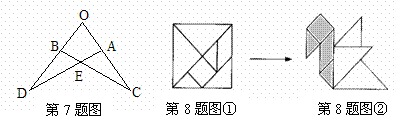
&8. 用边长为1的正方形纸板,制成一幅七巧板(如图①),将它拼成“小天鹅”图案
(如图②),其中阴影部分的面积是( )
 A.
A.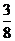 B.
B.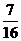 C.
C.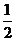 D.
D.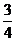
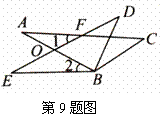
#9.如图所示,已知△ABC≌△EBD
求证:∠1=∠2
第二课时11.2.1三角形全等的条件(SSS)及其应用
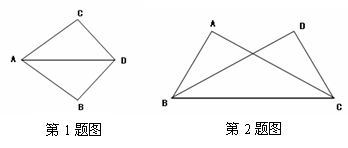
※1.如图所示,若AB=AC,DB=DC,根据 可得△ABD≌△ACD.
3. 已知△ABC≌△ADE,∠C=∠E,AB=AD,
则另外两组对应边为________,
另外两组对应角为________.
#4.若△MNP≌△NMQ,且MN=8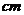 ,NP=7
,NP=7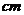 ,PM=6
,PM=6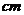 ,则MQ的长为( )
,则MQ的长为( )
A. 8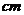 B. 7
B. 7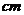 C. 6
C. 6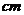 D.5
D.5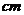
17.如图, ∠AOB是一个任意角,在边OA,OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与M,N重合,过角尺顶点C的射线OC便是∠AOB的平分线,为什么?
16.工人师傅要检查人字梁的∠B和∠C是否相等,但他手边没有量角器,只有一个刻度尺.他是这样操作的:
①分别在BA和CA上取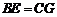 ;
;
②在BC上取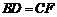 ;
;
③量出DE的长a米,FG的长b米.
如果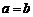 ,则说明∠B和∠C是相等的.他的这种做法合理吗?为什么?
,则说明∠B和∠C是相等的.他的这种做法合理吗?为什么?
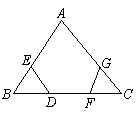
15.如图,已知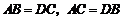 .求证:
.求证: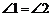 .
.
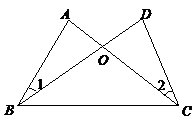
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com