5.反比例函数y= -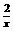的图象位于　　 (　　　 )

　 A、第一、二象限　　　 B、第一、三象限　　 C、第二、三象限　　 D、第二、四象限

4.若点(3,4)是反比例函数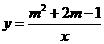图象上一点，则此函数图象必须经过点(　　 ).A(2，6)　 　B(2，-6)　 C(4，-3)　 　D.(－3，－4)

3.已知点A(-2，y₁)、B(-1，y₂)、C(3，y₃)都在反比例函数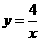的图象上，则　 A. y₁<y₂<y₃　　 B. y₃<y₂<y₁　　 C. y₃<y₁<y₂　　 D. y₂<y₁<y₃ (　　 )

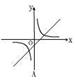
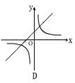
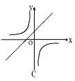
2.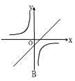在同一平面直角坐标系中，函数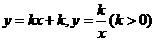的图像大致是

　　　　　　　　 (　　 )

1.已知正比例函数y=k₁x(k₁≠0)与反比例函数y=(k₂≠0)的图象有一个交点的坐标为(-2，-1)，则它的另一个交点的坐标是(　　 )

A. (2，1)　　　 　　　　 B. (-2，-1)　　　　 C. (-2，1)　　　　　 D. (2，-1)

如图3所示，结合表格中的数据回答问题：

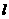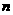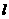(1)设图形的周长为，梯形的个数为，试写出与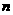的函数解析式．

(2)求当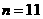时的图形的周长．

4．(10分)某市第五中学校办工厂今年产值是15万元，计划今后每年增加2万元．

(1)写出年产值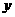(万元)与今后年数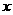之间的函数关系式．

(2)画出函数图象．

(3)求5年后的年产值．

3．(10分)已知水池中有800立方米的水，每小时抽50立方米．

(1)写出剩余水的体积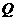立方米与时间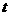(时)之间的函数关系式．

(2)写出自变量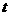的取值范围．

(3)10小时后，池中还有多少水？zk5u

(4)几小时后，池中还有100立方米的水？

2．(10分)按图2方式摆放餐桌和椅子．若用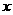来表示餐桌的张数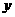，来表示可坐人数，则随着餐桌数的增加：

zk5u

(1)题中有几个变量？

(2)你能将其中的一个变量看成是另一个变量的函数吗？如果是，写出函数解析式．

Zk5u

1．(10分)如图1是襄樊地区一天的气温随时间变化的图象，根据图象回答：在这一天中：

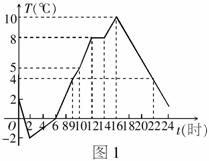(1)气温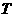(℃)　　　　　 (填“是”或“不是”)时间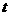(时)的函数．

(2)　　　 时气温最高，　　　 时气温最低，最高汽温是　　　 ℃，最低气温是　　　 ℃．

(3)10时的气温是　　　　　 ℃．

(4)　　　　 时气温是4℃．

(5)　　　　　 时间内，气温不断上升．

(6)　　　　 时间内，气温持续不变．